初中数学人教版九年级上册24.1.2 垂直于弦的直径课文配套ppt课件

这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径课文配套ppt课件，共20页。PPT课件主要包含了课堂目标，问题导入，模型讲解，模型总结，例题讲解，定直角三角形，定边长，勾股定理建立方程，应用练习，课堂总结等内容，欢迎下载使用。

能够理解垂径定理概念能够掌握垂径定理性质，构造直角三角形能够运用垂径定理构造直角三角形解决问题
问题：如图，⊙O的弦AB=8，P是劣弧AB中点，连结OP交AB于C，且0C=3，则⊙0的半径为（ ）
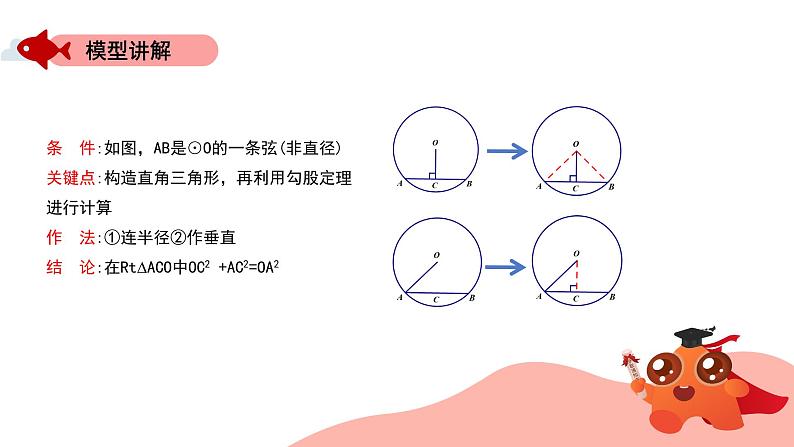
条 件:如图，AB是⊙O的一条弦(非直径)关键点:构造直角三角形，再利用勾股定理进行计算作 法:①连半径②作垂直结 论:在Rt∆ACO中OC2 +AC2=OA2
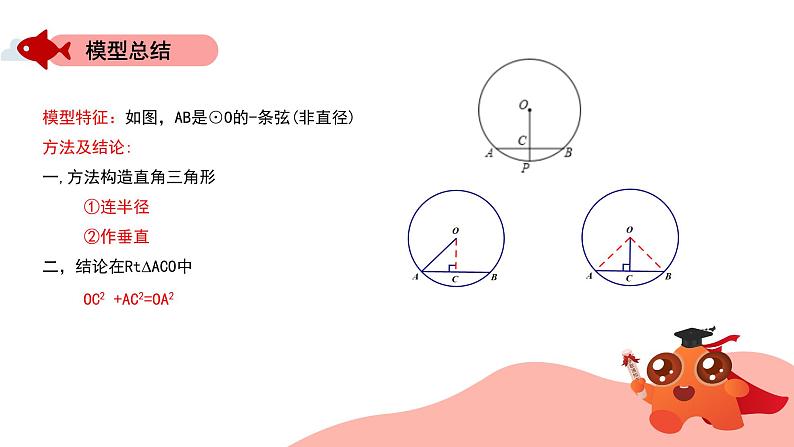
模型特征：如图，AB是⊙O的-条弦(非直径) 方法及结论:一,方法构造直角三角形 ①连半径 ②作垂直二，结论在Rt∆ACO中 OC2 +AC2=OA2
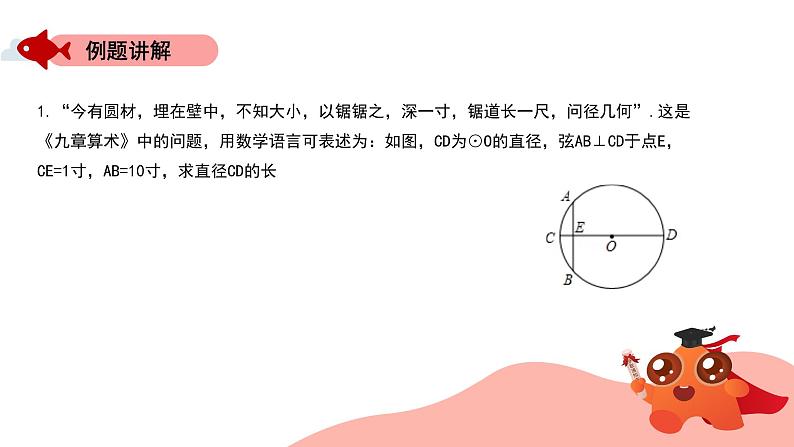
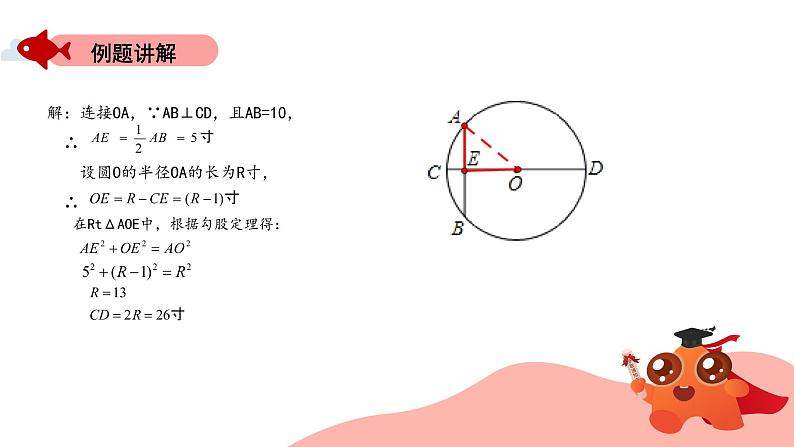
1.“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”.这是《九章算术》中的问题，用数学语言可表述为：如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1寸，AB=10寸，求直径CD的长
Rt∆AOE
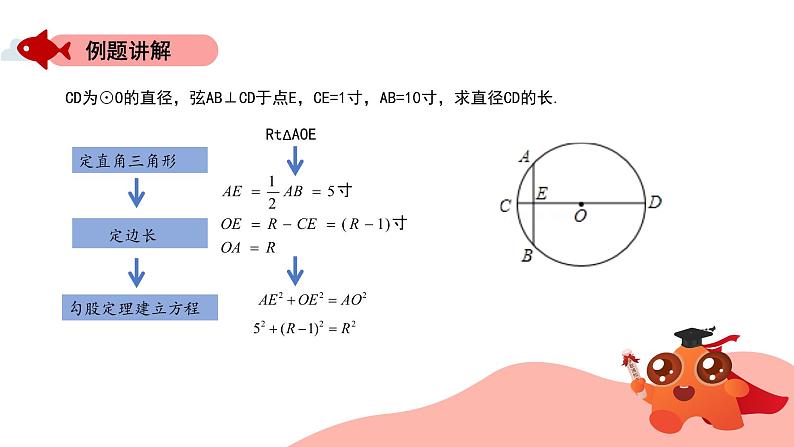
CD为⊙O的直径，弦AB⊥CD于点E，CE=1寸，AB=10寸，求直径CD的长.
解：连接OA，∵AB⊥CD，且AB=10， ∴ 设圆O的半径OA的长为R寸， ∴
在RtΔAOE中，根据勾股定理得：
2. 如图，⊙O的半径为10cm，弦AB//CD，AB=16cm，CD=12cm，圆心O位于AB，CD的上方，求AB和CD间的距离
1. 如图，⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM:OC=3:5，则AB的长为( )
2. 如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC= ( )
3. 如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径是________
方法技巧：①定直角三角形②定边长③利用勾股定理直接求或者列方程计算考法：求线段长（弦、弦心距、半径）