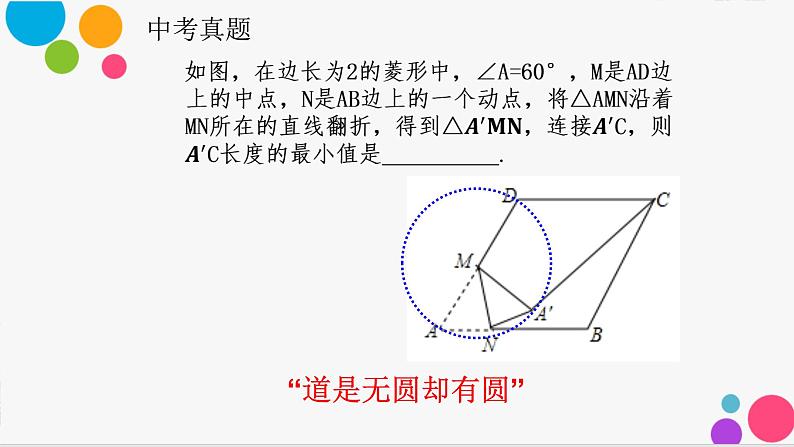
中考数学复习 构造圆 “圆”于条件，巧妙构造课件PPT

这是一份中考数学复习 构造圆 “圆”于条件，巧妙构造课件PPT，共15页。PPT课件主要包含了中考真题，圆的定义是什么，练习1，练习2，定线段对定角度，基本模型3等内容，欢迎下载使用。

在同一平面内，到定点的距离等于定长的点的集合叫做圆
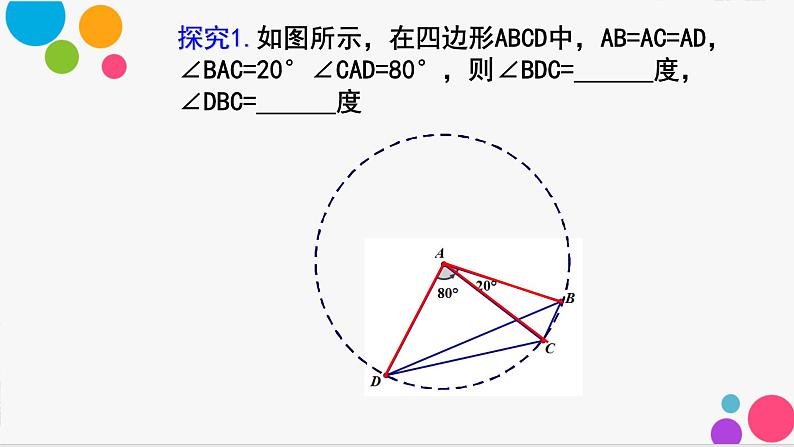
探究1.如图所示，在四边形ABCD中，AB=AC=AD，∠BAC=20°∠CAD=80°，则∠BDC=______度，∠DBC=______度
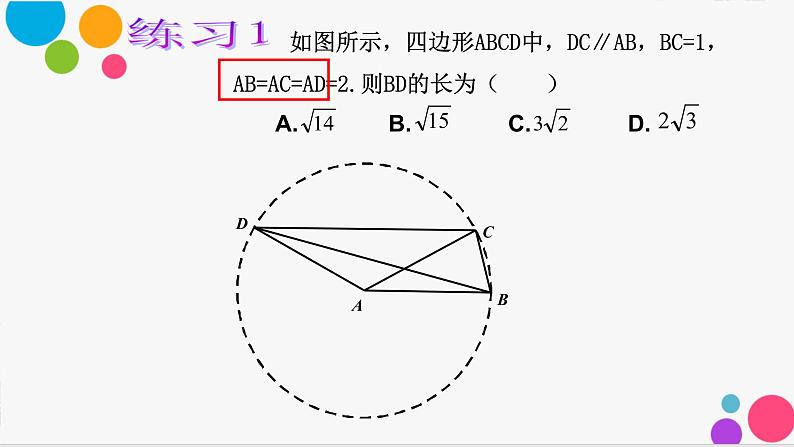
利用定义：等线段，共端点。
什么条件让你想到可以构造圆，可以构造圆的依据是什么？
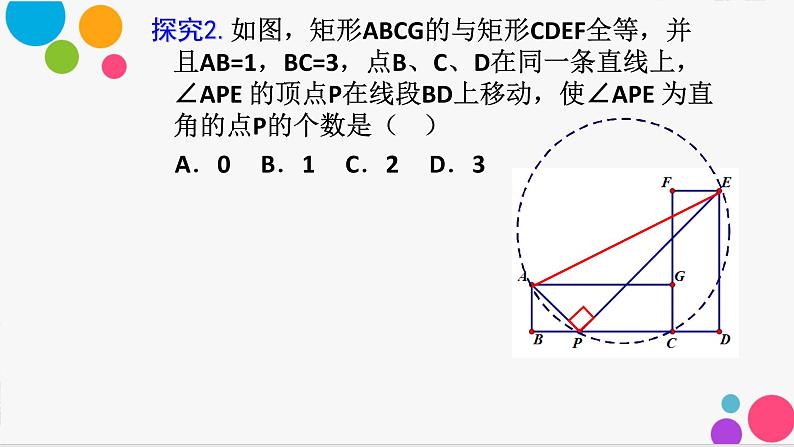
探究2.如图，矩形ABCG的与矩形CDEF全等，并且AB=1，BC=3，点B、C、D在同一条直线上，∠APE 的顶点P在线段BD上移动，使∠APE 为直角的点P的个数是（ ） A．0 B．1 C．2 D．3
利用性质：90°，对直径。
利用90°的圆周角所对弦是直径构造圆
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为______
探究3.在平面直角坐标系中，已知点A（4，0）、B（﹣6，0），点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为 ．
变式1：如果把∠BCA=45°改成∠BCA=30°，还会做吗？
基本模型1 基本模型2
运用四点共圆的判断方法
同底同侧张角相等的三角形各定点共圆
一个四边形的一组对角互补，则它的四个顶点共圆
探究四：如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，且DE=2CE,过点C作CF⊥BE,垂足为F，连接OF，则OF的长为？