2020-2021学年北京市朝阳区十七中教育集团八下期中数学试卷

这是一份2020-2021学年北京市朝阳区十七中教育集团八下期中数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 式子 x−1 在实数范围内有意义，则 x 的取值范围是
A. x>0B. x≥−1C. x≥1D. x≤1

2. 如图，菱形花坛 ABCD 的面积为 12 平方米，其中沿对角线 AC 修建的小路长为 4 米，则沿对角线 BD 修建的小路长为
A. 6 米B. 3 米C. 8 米D. 10 米

3. 在平行四边形 ABCD 中，∠A=40∘，则 ∠C 的度数为
A. 50∘B. 140∘C. 40∘D. 130∘

4. 下列关于平行四边形 ABCD 的叙述，正确的是
A. 若 AC=BD，则平行四边形 ABCD 是矩形
B. 若 AB=AD，则平行四边形 ABCD 是正方形
C. 若 AB⊥BC，则平行四边形 ABCD 是菱形
D. 若 AC⊥BD，则平行四边形 ABCD 是正方形

5. 如图，在正方形 ABCD 中，E 为 DC 边上的点，连接 BE，将 △BCE 绕点 C 顺时针方向旋转 90∘ 得到 △DCF，连接 EF．若 ∠BEC=60∘，则 ∠EFD 的度数为
A. 10∘B. 15∘C. 20∘D. 25∘

6. 若直角三角形的三边长分别为 2，4，x，则 x 的值为
A. 3B. 25C. 23D. 25 或 23

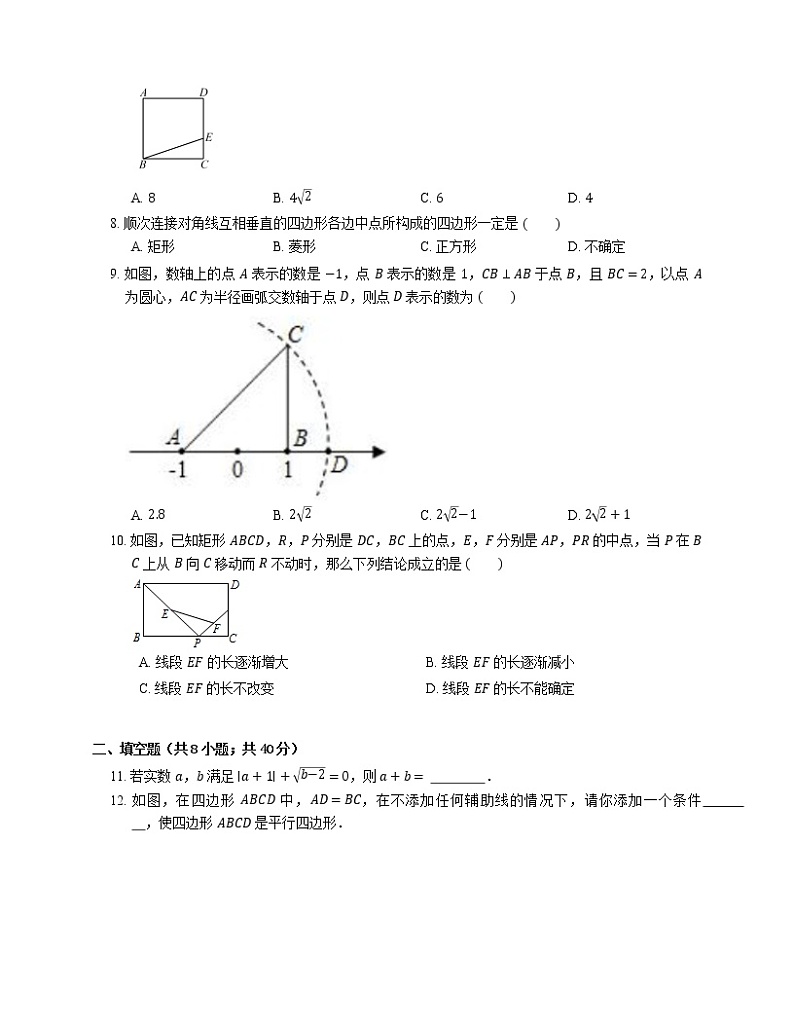
7. 如图，在正方形 ABCD 中，E 是 CD 上的点，若 BE=3，CE=1，则正方形 ABCD 的对角线的长为
A. 8B. 42C. 6D. 4

8. 顺次连接对角线互相垂直的四边形各边中点所构成的四边形一定是
A. 矩形B. 菱形C. 正方形D. 不确定

9. 如图，数轴上的点 A 表示的数是 −1，点 B 表示的数是 1，CB⊥AB 于点 B，且 BC=2，以点 A 为圆心，AC 为半径画弧交数轴于点 D，则点 D 表示的数为
A. 2.8B. 22C. 22−1D. 22+1

10. 如图，已知矩形 ABCD，R，P 分别是 DC，BC 上的点，E，F 分别是 AP，PR 的中点，当 P 在 BC 上从 B 向 C 移动而 R 不动时，那么下列结论成立的是
A. 线段 EF 的长逐渐增大B. 线段 EF 的长逐渐减小
C. 线段 EF 的长不改变D. 线段 EF 的长不能确定

二、填空题（共8小题；共40分）
11. 若实数 a，b 满足 ∣a+1∣+b−2=0，则 a+b= ．

12. 如图，在四边形 ABCD 中，AD=BC，在不添加任何辅助线的情况下，请你添加一个条件 ，使四边形 ABCD 是平行四边形．

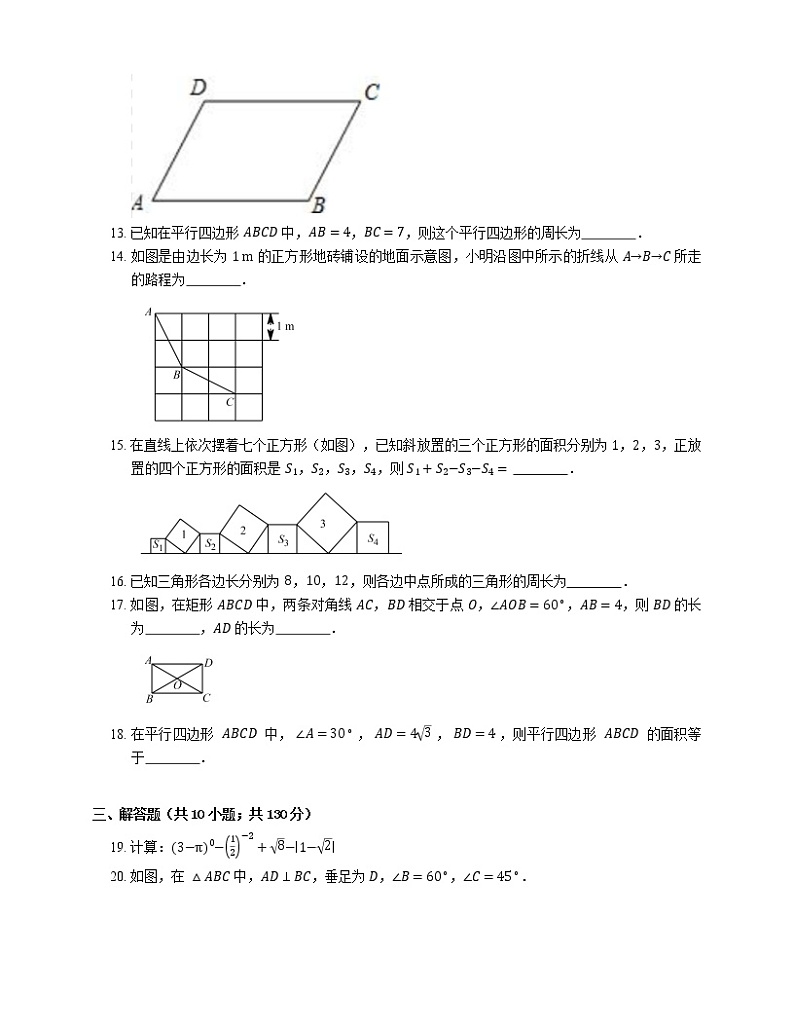
13. 已知在平行四边形 ABCD 中，AB=4，BC=7，则这个平行四边形的周长为 ．

14. 如图是由边长为 1 m 的正方形地砖铺设的地面示意图，小明沿图中所示的折线从 A→B→C 所走的路程为 ．

15. 在直线上依次摆着七个正方形（如图），已知斜放置的三个正方形的面积分别为 1，2，3，正放置的四个正方形的面积是 S1，S2，S3，S4，则 S1+S2−S3−S4= ．

16. 已知三角形各边长分别为 8，10，12，则各边中点所成的三角形的周长为 ．

17. 如图，在矩形 ABCD 中，两条对角线 AC，BD 相交于点 O，∠AOB=60∘，AB=4，则 BD 的长为 ，AD 的长为 ．

18. 在平行四边形 ABCD 中， ∠A=30∘ ， AD=43 ， BD=4 ，则平行四边形 ABCD 的面积等于 ．

三、解答题（共10小题；共130分）
19. 计算：3−π0−12−2+8−1−2

20. 如图，在 △ABC 中，AD⊥BC，垂足为 D，∠B=60∘，∠C=45∘．
（1）求 ∠BAC 的度数；
（2）若 BD=2，求 CD 的长．

21. 已知：如图，平行四边形 ABCD 中，E，F 分别是 AD，BC 上的点，且 AE=CF，求证四边形 BFDE 是平行四边形．

22. 已知：如图，AB=4，BD=12，CD=13，AC=3，AB⊥AC，求证：BC⊥BD．

23. 已知：如图，在平行四边形 ABCD 中，M 为 BC 中点，∠MAD=∠MDA．
求证：四边形 ABCD 是矩形．

24. 如图，E 为正方形 ABCD 内一点，且三角形 EBC 是等边三角形，求 ∠EAD 的度数．

25. 如图，在平行四边形 ABCD 中，AC=8，BD=12，点 E，F 在对角线 BD 上，点 E 从点 B 出发以 1 个单位每秒的速度向点 D 运动，同时点 F 从点 D 出发以相同速度向点 B 运动，到端点时运动停止，运动时间为 t 秒．
（1）求证：四边形 AECF 为平行四边形；
（2）求 t 为何值时，四边形 AECF 为矩形．

26. 如图，在矩形 ABCD 中，对角线 AC，BD 相交于点 O，点 O 关于直线 CD 的对称点为 E，连接 DE，CE．
（1）求证：四边形 ODEC 为菱形；
（2）连接 OE，若 BC=22，求 OE 的长．

27. 如图，将一张矩形纸片 ABCD 沿直线 MN 折叠，使点 C 落在点 A 处，点 D 落在点 E 处，直线 MN 交 BC 于点 M，交 AD 于点 N．
（1）求证：CM=CN；
（2）若 △CMN 的面积与 △CDN 的面积比为 3:1，且 CD=4，求线段 MN 的长．

28. 如图，O 为菱形 ABCD 对角线的交点，M 是射线 CA 上的一个动点（点 M 与点 C，O，A 都不重合），过点 A，C 分别向直线 BM 作垂线段，垂足分别为 E，F，连接 OE，OF．
（1）①依据题意补全图形；
②猜想 OE 与 OF 的数量关系为 ．
（2）小东通过观察、实验发现点 M 在射线 CA 上运动时，（1）中的猜想始终成立．
小东把这个发现与同学们进行交流，通过讨论，形成了证明（1）中猜想的几种想法：
想法 1：由已知条件和菱形对角线互相平分，可以构造与 △OAE 全等的三角形，从而得到相等的线段，再依据直角三角形斜边中线的性质，即可证明猜想；
想法 2：由已知条件和菱形对角线互相垂直，能找到两组共斜边的直角三角形，例如其中的一组 △OAB 和 △EAB，再依据直角三角形斜边中线的性质，菱形四边相等，可以构造一对以 OE 和 OF 为对应边的全等三角形，即可证明猜想．
⋯⋯
请你参考上面的想法，帮助小东证明（1）中的猜想（一种方法即可）．
（3）当 ∠ADC=120∘ 时，请直接写出线段 CF，AE，EF 之间的数量关系是 ．
答案
第一部分
1. C
2. A
3. C
4. A
5. B
6. D
7. D
8. A
9. C
10. C
【解析】∵ EF 是 △APR 的中位线，
∴ EF=12AR．
∵ AR 的长度不变，
∴ EF 的长也不改变．
第二部分
11. 1
12. AD∥BC（AB=CD）
13. 22
14. 25
15. −2
16. 15
17. 8，43
18. 163 或 83
第三部分
19. 3−π0−12−2+8−1−2=1−4+22−2−1=−3+22−2+1=2−2.
20. （1） ∠BAC=180∘−60∘−45∘=75∘．
（2） ∵AD⊥BC，
∴△BDC 是直角三角形，
又 ∵∠B=60∘，
∴∠BAD=30∘，
∴AB=2BD=4，
BD2+AD2=AB2，
∴AD=23
又 ∵∠C=45∘，
∴CD=AD=23．
21. ∵ 四边形 ABCD 是平行四边形，
∴AD∥BC，AD=BC，
∵AE=CF，
∴AD−AE=BC−CF，
∴ED=BF，
又 ∵AD∥BC，
∴ 四边形 BFDE 是平行四边形．
22. ∵AB=3，AC=4，AB⊥AC，
∴BC=5．
∵BD=12，CD=13，BC2+BD2=52+122=132=CD2，
∴∠CBD=90∘．
∴BC⊥BD．
23. ∵ 四边形 ABCD 是平行四边形，
∴AB=DC，AB∥DC，
∴∠B+∠C=180∘，
∵M 是 BC 的中点，
∴BM=CM，
∵∠MDA=∠MAD，
∴AM=DM，
在 △ABM 和 △DCM 中，
AB=DC,BM=CM,AM=DM,
∴△ABM≌△DCMSSS，
∴∠B=∠C，
∴∠B=∠C=90∘，
∴ 四边形 ABCD 是矩形．
24. △EBC 是等边三角形，
∴∠ABE=∠ECD=90∘−60∘=30∘，
EB=BC=AB，
所以，△ABE 是等腰三角形，
所以 ∠AEB=∠BEA=150∘÷2=75∘，
所以，∠EAD=15∘．
25. （1） 在平行四边形 ABCD 中，
∵OA=OC，OB=OD，
∵E 从点 B 出发以 1 个单位每秒的速度向点 D 运动，同时点 F 从点 D 出发以相同速度向点 B 运动，
∴CE=AF，
∴BE=DF，
∴OE=OF，
∴ 四边形 AECF 为平行四边形．
（2） 当 t=2 或 t=10 时以点 A，C，E，F 为顶点的四边形为矩形；
理由：由矩形的性质知 OE=OF，OA=OC，要使 ∠EAF 是直角，只需 OE=OF=OA=12AC=4 cm．
则 ∠1=∠2，∠3=∠4，
∵∠1+∠2+∠3+∠4=180∘，
∴2∠2+2∠3=180∘，
∴∠2+∠3=90∘，即 ∠EAF=90∘．
此时 BE=DF=12BD−EF=1212−8=2 cm 或 BE=DF=12−2=10 cm．
26. （1） ∵ 四边形 ABCD 是矩形，
∴OD=OC，
∵ 点 O 关于直线 CD 的对称点为 E，
∴OD=ED，OC=EC，
∴OD=DE=EC=CO，
∴ 四边形 ODEC 为菱形．
（2） 由（1）知四边形 ODEC 为菱形，连接 OE，
∴CE∥OD 且 CE=OD，
∴CE∥BO 且 CE=BO，
∴ 四边形 OBCE 为平行四边形，
∴OE=BC=22．
27. （1） 由折叠的性质可得：∠ANM=∠CNM，
∵ 四边形 ABCD 是矩形，
∴AD∥BC，
∴∠ANM=∠CMN，
∴∠CMN=∠CNM，
∴CM=CN．
（2） 如图，过点 N 作 NH⊥BC 于点 H，
则四边形 NHCD 是矩形，
∴HC=DN，NH=DC，
∵△CMN 的面积与 △CDN 的面积比为 3:1，
∴MC=3ND=3HC，
∴MH=2HC，
设 DN=x，则 HC=x，MH=2x，
∴CM=3x=CN，
在 Rt△CDN 中，DC=22x=4，
∴x=2，
∴HM=22，
在 Rt△MNH 中，MN=MH2+NH2=8+16=26．
28. （1） ①补全的图形如图所示．
② OE=OF．
（2） 法一：
如图 1，
延长 EO 交 FC 的延长线于点 N，
∵ 四边形 ABCD 是菱形，
∴AO=CO．
∵AE⊥BM，CF⊥BM，
∴AE∥CF．
∴∠AEO=∠CNO．
又 ∵∠AOE=∠CON，
∴△AOE≌△CON．
∴OE=ON=12EN．
∵Rt△EFN 中，O 是斜边 EN 的中点，
∴OF=12EN
∴OE=OF．
【解析】法二：
如图 2，
取线段 AB，BC 的中点 P，Q，连接 OP，PE，OQ，QF，
∵ 四边形 ABCD 是菱形，
∴AB=BC，AC⊥BD．
∵P，Q 是 AB，BC 的中点，
∴OP=PB=12AB，OQ=QB=12BC，
∴OP=OQ．
同理，PE=QF．
∵OP=PB，PE=PB，
∴∠OPA=2∠OBA，∠EPA=2∠EBA．
∴∠OPA+∠EPA=2∠OBA+2∠EBA，即 ∠OPE=2∠OBE．
同理，∠OQF=2∠OCF．
∵AC⊥BD，CF⊥BM，
∴∠OBE+∠OMB=∠OCF+∠OMB=90∘．
∴∠OBE=∠OCF．
∴∠OPE=∠OQF．
∴△OPE≌△OQF．
∴OE=OF．
（3） EF=3CF+AE
【解析】如图 1，
由（2）方法一、得出 △AOE≌△CON，
∴AE=CN，OE=ON，
由（2）知，OE=OF，
∴OF=ON，
∵ 四边形 ABCD 是菱形，
∴∠ABC=∠ADC=120∘，
∴∠ABE+∠CBF=60∘，
∵∠AOB=∠AEB=90∘，
∴ 点 A，E，B，O 共圆，
∴∠AOE=∠ABE，
同理：∠COF=∠CBF，
∴∠NOF=∠NOC+∠COF=∠AOE+∠CBF=∠ABE+∠CBF=60∘，
∵OF=ON，
∴△FON 是等边三角形，
∴∠ONF=60∘，
∴∠FEN=30∘，
在 Rt△EFN 中，∠FEN=30∘，
∴EF=3FN=3CF+CN=3CF+AE．