2019_2020学年福州市鼓楼区文博中学八上期末数学试卷

这是一份2019_2020学年福州市鼓楼区文博中学八上期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 使分式 2x−1 有意义，则 x 的取值范围是
A. x≠1B. x=1C. x≤1D. x≥1

2. 下列各式计算正确的是
A. −3−2=−19B. 18−32=−2
C. a0=1D. −22=−2

3. 用 a，b，c 作三角形的三边，其中不能构成直角三角形的是
A. a=1，b=2，c=3B. a=2，b=3，c=4
C. a=12，b=5，c=13D. a=7，b=2，c=3

4. 已知平行四边形 ABCD 中，∠A+∠C=200∘，则 ∠B 的度数是
A. 100∘B. 160∘C. 80∘D. 60∘

5. 一艘船顺流航行 s 千米用了 x 小时，如果逆流航速是顺流航速的 nm，那么这艘船逆流航行 t 小时走的路程是
A. sntxmB. smtxnC. stxD. xsntm

6. 如图，平行四边形 ABCD 的对角线交于点 O，且 AB=5，△OCD 的周长为 23，则平行四边形 ABCD 的两条对角线的和是
A. 18B. 28C. 36D. 46

7. 甲、乙两地之间的高速公路全长 200 千米，比原来国道的长度减少了 20 千米．高速公路通车后，某长途汽车的行驶速度提高了 45 千米/时，从甲地到乙地的行驶时间缩短了一半．设该长途汽车在原来国道上行驶的速度为 x 千米/时，根据题意，下列方程正确的是
A. 200x=180x−45×12B. 200x=220x−45×12
C. 200x+45=180x×12D. 200x+45=220x×12

8. 关于 x 的分式方程 xx−1−2=mx−1 无解，则 m 的值是
A. 1B. 0C. 2D. −2

9. 如图，在 △ABC 和 △BDE 中，点 C 在边 BD 上，边 AC 交边 BE 于点 F．若 AC=BD，AB=ED，BC=BE，则 ∠ACB 等于
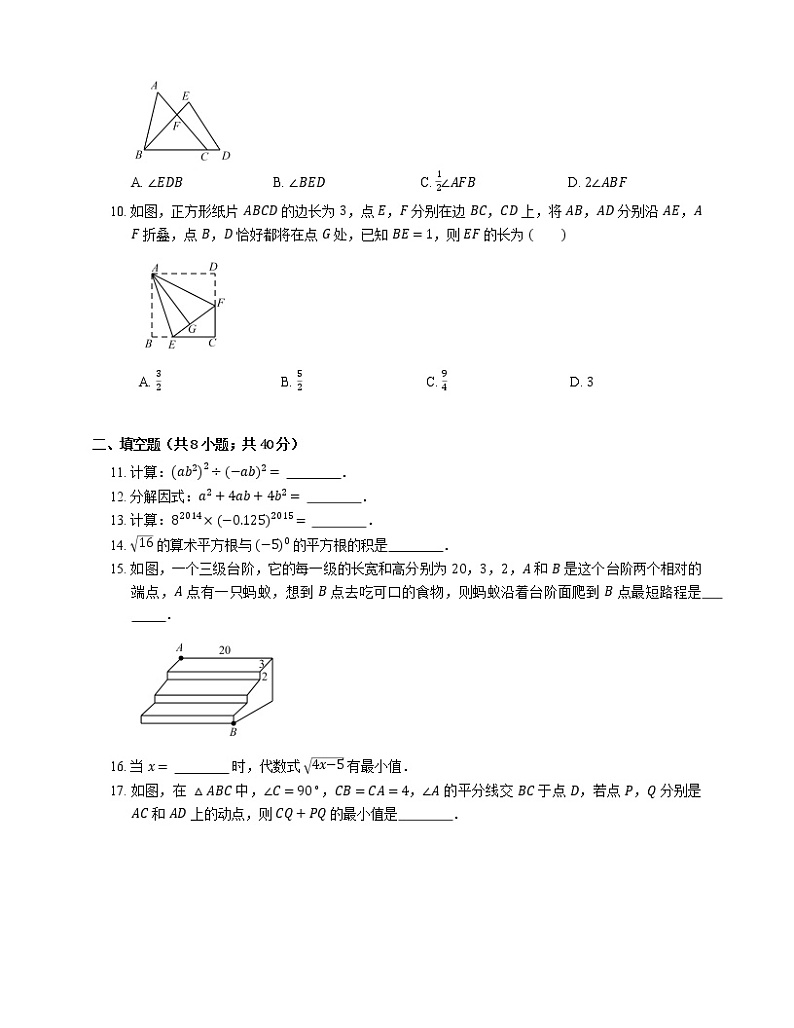
A. ∠EDBB. ∠BEDC. 12∠AFBD. 2∠ABF

10. 如图，正方形纸片 ABCD 的边长为 3，点 E，F 分别在边 BC，CD 上，将 AB，AD 分别沿 AE，AF 折叠，点 B，D 恰好都将在点 G 处，已知 BE=1，则 EF 的长为
A. 32B. 52C. 94D. 3

二、填空题（共8小题；共40分）
11. 计算：ab22÷−ab2= ．

12. 分解因式：a2+4ab+4b2= ．

13. 计算：82014×−0.1252015= ．

14. 16 的算术平方根与 −50 的平方根的积是 ．

15. 如图，一个三级台阶，它的每一级的长宽和高分别为 20，3，2，A 和 B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到 B 点去吃可口的食物，则蚂蚁沿着台阶面爬到 B 点最短路程是 ．

16. 当 x= 时，代数式 4x−5 有最小值．

17. 如图，在 △ABC 中，∠C=90∘，CB=CA=4，∠A 的平分线交 BC 于点 D，若点 P，Q 分别是 AC 和 AD 上的动点，则 CQ+PQ 的最小值是 ．

18. 如图，△ABC 和 △FPQ 均是等边三角形，点 D，E，F 分别是 △ABC 三边的中点，点 P 在 AB 边上，连接 EF，QE．若 AB=6，PB=1，则 QE= ．

三、解答题（共8小题；共104分）
19. （1）计算：−12015+π−30+12−1−1−22；
（2）化简：239x+6x4−2x1x．

20. 解方程：
（1）6x−3−2x−34x−3=1；
（2）1x+3−23−x=9x2−9．

21. 先化简，再求值：x+2x2−2x−x−1x2−4x+4÷x−4x2−2x，其中 x=5．

22. 如图，在平行四边形 ABCD 中，对角线 AC,BD 交于点 O，经过点 O 的直线交 AB 于 E，交 CD 于 F．求证：OE=OF．

23. 八年级学生到距离学校 15 千米的农科所参观，一部分学生骑自行车先走，走了 40 分钟后，其余同学乘汽车出发，结果两者同时到达．若汽车的速度是骑自行车同学速度的 3 倍，求骑自行车同学的速度?

24. 阅读下面的文字，解答问题．
大家知道 2 是无理数，而无理数是无限不循环小数，因此 2 的小数部分我们不可能全部地写出来，但是由于 1＜2＜2，所以 2 的整数部分为 1，将 2 减去其整数部分 1，差就是小数部分 2−1，根据以上的内容，解答下面的问题：
（1）5 的整数部分是 ，小数部分是 ；
（2）1+2 的整数部分是 ，小数部分是 ；
（3）若设 2+3 的整数部分是 x，小数部分是 y，求 x−3y

25. 已知将边长分别为 a 和 2ba>b 的长方形分割成四个全等的直角三角形，如图 1，再用这四个三角形拼成如图 2 所示的正方形，中间形成一个正方形的空洞．经测量得长方形的面积为 24，正方形的边长为 5．试通过你获取的信息，求 a2+b2 和 a2−b2 的值．

26. 如图，△ABC 中，D 是 BC 的中点，AB=43，AC=23，AD=3，求 BC 的长及 △ABC 的面积．
答案
第一部分
1. A【解析】根据题意得：x−1≠0，解得 x≠1．
2. B【解析】A．−3−2=19，故本选项错误；
B．18−32=32−42=−2，正确；
C．a0=1，此时 a≠0，故本选项错误；
D．−22=2，故本选项错误．
3. B【解析】12+22=32，则A能构成直角三角形；
22+32≠42，则B不能构成直角三角形；
122+52=132，则C能构成直角三角形；
22+32=72，则D能构成直角三角形．
4. C
5. A
【解析】根据题意得：顺流速度为 sx 千米/小时，逆流速度为 snxm 千米/小时，
则这艘船逆流航行 t 小时走了 sntxm 千米．
6. C
7. D【解析】设该长途汽车在原来国道上行驶的速度为 x 千米/时，根据题意得 200x+45=220x×12．
8. A【解析】去分母得 x−2x−1=m，解得 x=2−m．
∵ 当 x=1 时分母为 0，方程无解，
∴2−m=1，即 m=1 时方程无解．
9. C【解析】在 △ABC 和 △DEB 中，
AC=DB,AB=DE,BC=EB,
∴△ABC≌△DEB SSS，
∴∠ACB=∠DBE．
∵∠AFB 是 △BFC 的外角，
∴∠ACB+∠DBE=∠AFB，
∠ACB=12∠AFB．
10. B
【解析】∵ 正方形纸片 ABCD 的边长为 3，
∴∠C=90∘，BC=CD=3，
根据折叠的性质得：EG=BE=1，GF=DF，
设 DF=x，
则 EF=EG+GF=1+x，FC=DC−DF=3−x，EC=BC−BE=3−1=2，
在 Rt△EFC 中，EF2=EC2+FC2，
即 x+12=22+3−x2，
解得：x=32，
∴DF=32，EF=1+32=52．
第二部分
11. b2
12. a+2b2
【解析】a2+4ab+4b2=a+2b2．
13. −0.125
14. ±2
【解析】∵ 16=4，
∴ 16 的算术平方根为 2，
∵ −50=1，
∴ −50 的平方根为 ±1，
则 16 的算术平方根与 −50 的平方根的积是 ±2．
15. 25
16. 54
【解析】∵4x−5≥0，
∴x≥54，
当 x=54 时，4x−5 的最小值为 0．
17. 22
【解析】如图，作点 P 关于直线 AD 的对称点 Pʹ，连接 CPʹ 交 AD 于点 Q，
则 CQ+PQ=CQ+PʹQ=CPʹ．
∵ 根据对称的性质知 △APQ≌△APʹQ，
∴∠PAQ=∠PʹAQ．
又 ∵AD 是 ∠A 的平分线，点 P 在 AC 边上，点 Q 在直线 AD 上，
∴∠PAQ=∠BAQ，
∴∠PʹAQ=∠BAQ，
∴ 点 Pʹ 在边 AB 上．
∵ 当 CPʹ⊥AB 时，线段 CPʹ 最短．
∵ 在 △ABC 中，∠C=90∘，CB=CA=4，
∴AB=CB2+CA2=42，且当点 Pʹ 是斜边 AB 的中点时，CPʹ⊥AB，
此时 CPʹ=12AB=22，即 CQ+PQ 的最小值是 22．
18. 2
【解析】如图所示，连接 FD．
根据中位线知识，△FQE 和 △FPD 全等，所以 EQ=DP，因为 AB=6，PB=1，D 为 AB 中点，所以 DP=EQ=2．
第三部分
19. （1） 原式=−1+1+2−2+1=3−2.
（2） 原式=2x+3x−2x=3x.
20. （1） 去分母：
24−2x−3=4x−3.
去括号：
24−2x+3=4x−12.
合并同类项：
6x=39.
系数化为 1：
x=132.
经检验：x=132 是原方程的解．
（2） 去分母：
x−3+2x+3=9.
去括号：
x−3+2x+6=9.
合并同类项：
3x=6.
系数化为 1：
x=2.
经检验：x=2 是原方程的解．
21. 原式=x+2xx−2−x−1x−22×xx−2x−4=x2−4−x2+xxx−22×xx−2x−4=1x−2.
当 x=5 时，原式=13．
22. ∵ 四边形 ABCD 是平行四边形，
∴OA=OC，AB∥CD，
∴∠OAE=∠OCF．
∵∠AOE=∠COF，
∴△OAE≌△OCF（ASA）．
∴OE=OF．
23. 设骑自行车的速度是 x 千米/小时，
15x=153x+4060.
解得，
x=15.
经检验 x=15 是方程的解，且符合实际意义．
答：骑自行车的同学的速度是 15 千米/小时．
24. （1） 2；5−2
【解析】∵2＜5＜3，
∴5 的整数部分是 2，小数部分是 5−2 .
（2） 2；1+2−2=2−1
【解析】∵1＜2＜2，
∴2＜1+2＜3，
∴1+2 的整数部分是 2，小数部分是 1+2−2=2−1 .
（3） ∵1＜3＜2，
∴3＜2+3＜4，
∴x=3，y=2+3−3=3−1，
∴x−3y=3−33−1=3．
25. 根据题意得 a2+b2=52=25，a⋅2b=24，
∴a2+b2+2ab=49，
∴a+b=7，
∴a2+b2−2ab=1，
∵a>b，
∴a−b=1，
∴a2−b2=a+ba−b=7×1=7，
∴a2+b2=25，a2−b2=7．
26. 延长 AD 到 E，使 DE=AD=3，连接 BE，CE，如图．
∵ D 是 BC 的中点，
∴ CD=BD，
∴ 四边形 ABEC 是平行四边形，
∴ AB∥CE，EB=CA=23，
∵ 62+232=432，即 AE2+AC2=EC2，
∴ ∠EAC=90∘，
∴ CD=AD2+AC2=32+232=21，
∴ BC=2CD=221，
∴ S△ABC=2S△ACD=2×12AC⋅AD=23×3=63．
综上所述，BC 的长度为 221，△ABC 的面积是 63．