2020-2021年河北省唐山市九年级上学期数学第二次月考试卷

这是一份2020-2021年河北省唐山市九年级上学期数学第二次月考试卷，共12页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 九年级上学期数学第二次月考试卷
一、单项选择题
2=-5x时，得x=-5，那么他漏掉的一个根是〔  〕
A. x=-5                                     B. x=0                                     C. x=-1                                     D. x=1
以下四张卡片中任取一张，卡片上的图形是中心对称图形的概率为〔    〕

A. 0                                          B.                                           C.                                           D. 
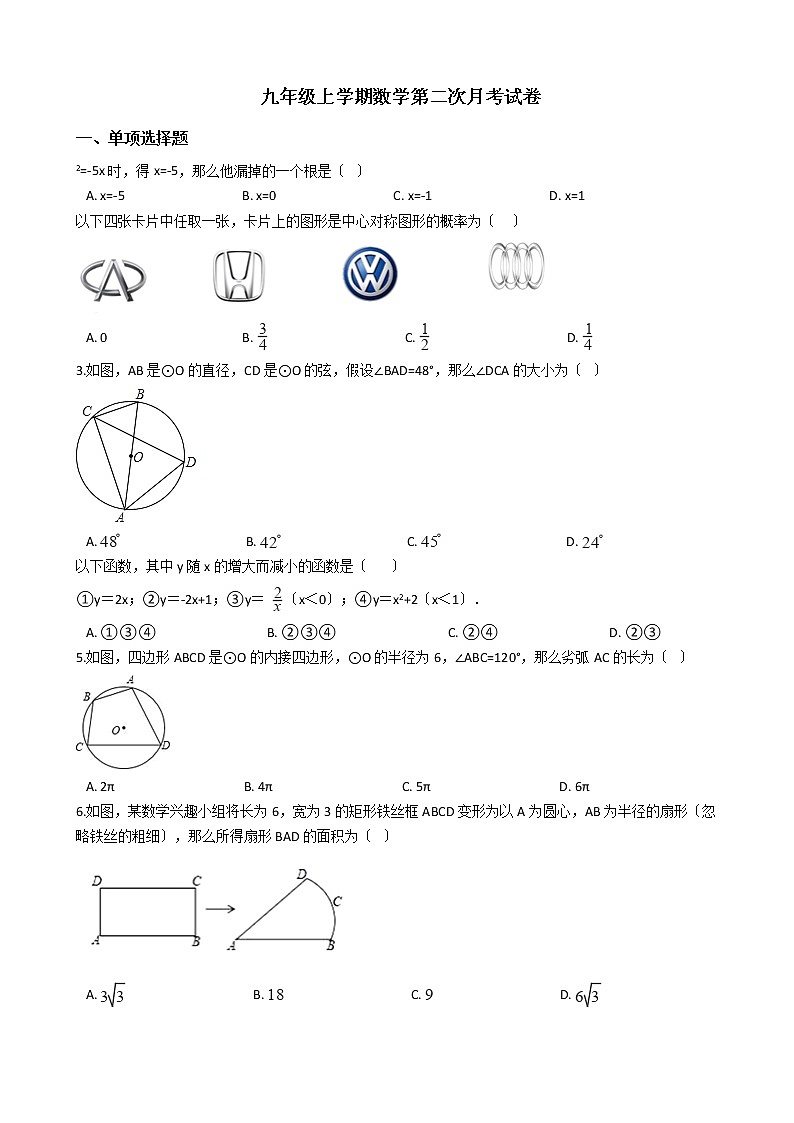
3.如图，AB是⊙O的直径，CD是⊙O的弦，假设∠BAD=48°，那么∠DCA的大小为〔  〕

A.                                        B.                                        C.                                        D. 
以下函数，其中y随x的增大而减小的函数是〔      〕
①y＝2x；②y＝-2x+1；③y＝ 〔x＜0〕；④y＝x2+2〔x＜1〕．
A. ①③④                                  B. ②③④                                  C. ②④                                  D. ②③
5.如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为6，∠ABC=120°，那么劣弧AC的长为〔  〕

A. 2π                                        B. 4π                                        C. 5π                                        D. 6π
6.如图，某数学兴趣小组将长为6，宽为3的矩形铁丝框ABCD变形为以A为圆心，AB为半径的扇形〔忽略铁丝的粗细〕，那么所得扇形BAD的面积为〔  〕

A.                                         B.                                         C.                                         D. 
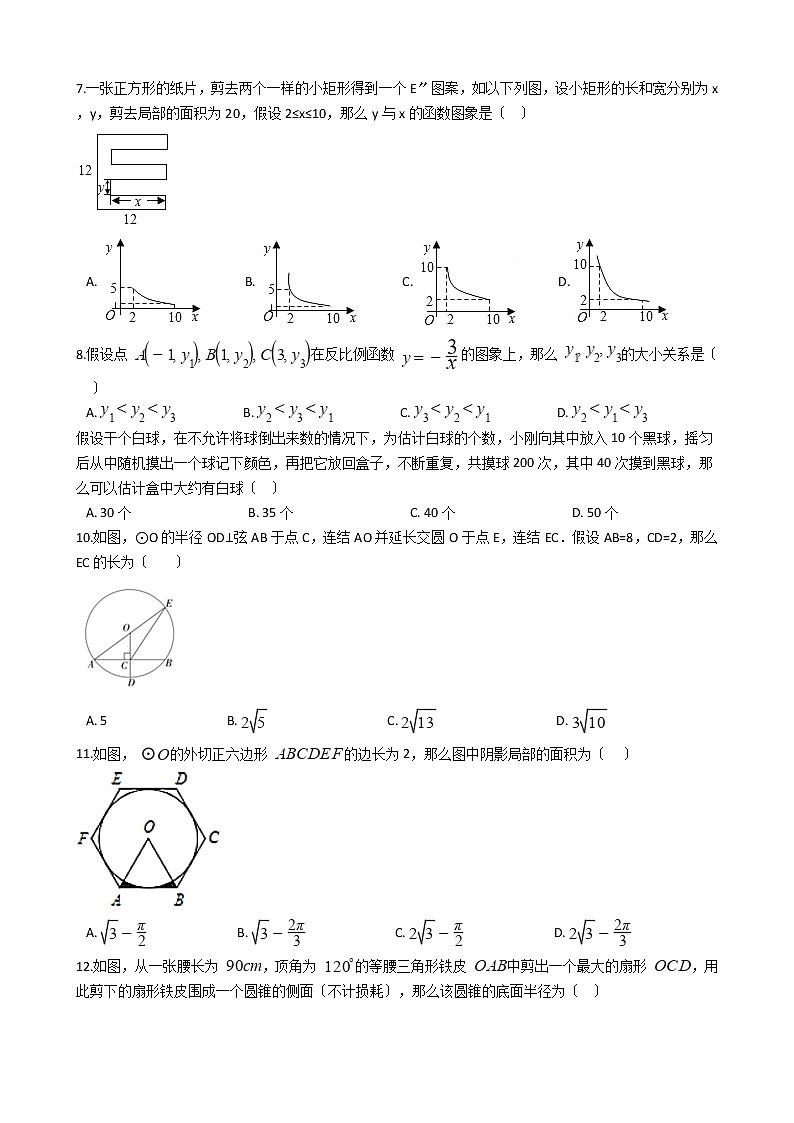
7.一张正方形的纸片，剪去两个一样的小矩形得到一个E〞图案，如以下列图，设小矩形的长和宽分别为x，y，剪去局部的面积为20，假设2≤x≤10，那么y与x的函数图象是〔   〕

A.              B.              C.              D. 
8.假设点 在反比例函数 的图象上，那么 的大小关系是〔    〕
A.                      B.                      C.                      D. 
假设干个白球，在不允许将球倒出来数的情况下，为估计白球的个数，小刚向其中放入10个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子，不断重复，共摸球200次，其中40次摸到黑球，那么可以估计盒中大约有白球〔   〕
A. 30个                                    B. 35个                                    C. 40个                                    D. 50个
10.如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交圆O于点E，连结EC．假设AB=8，CD=2，那么EC的长为〔       〕

A. 5                                     B.                                      C.                                      D. 
11.如图， 的外切正六边形 的边长为2，那么图中阴影局部的面积为〔    〕

A.                            B.                            C.                            D. 
12.如图，从一张腰长为 ，顶角为 的等腰三角形铁皮 中剪出一个最大的扇形 ，用此剪下的扇形铁皮围成一个圆锥的侧面〔不计损耗〕，那么该圆锥的底面半径为〔   〕

A.                                   B.                                   C.                                   D. 
13.如图， 的顶点 在反比例函数 的图像上，顶点 在 轴上， 轴，假设点 的坐标为 ， ，那么 的值为〔    〕

A. 4                                          B. -4                                          C. 7                                          D. -7
二、填空题
14.在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球，搅匀后从中随机摸出2个球，那么摸出的两个球恰好一红一白的概率是________．
15.如图，在平面直角坐标系中，直线y＝-3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形，点D恰好在双曲线上 ，那么k值为________．

16.如图， 的半径为2，圆心P在抛物线 上运动；当 与x轴相切时；圆心P的坐标为________.

17.如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，那么△ABC的外心和内心之间的距离为________．

三、解答题
如以下列图．将卡片洗匀后,反面朝上放置在桌面上．

〔1〕求随机抽取一张卡片,恰好得到数字2的概率;
〔2〕小贝和小晶想用以上四张卡片做游戏,游戏规那么见信息图．你认为这个游戏公平吗?请用列表法或画树形图法说明理由．
19.在平面直角坐标系xOy中，直线 与双曲线 相交于点 ．

〔1〕求反比例函数的表达式；
〔2〕画出双曲线的示意图；
〔3〕假设另一个交点B的坐标为 ，那么n=________；当 时，x的取值范围________；
〔4〕观察反比例函数的图象，当y2≤3时，自变量x的取值范围是________．
20.如图，在Rt△ABC中，∠B＝30°，∠ACB＝90°，延长CA到O ， 使AO＝AC ， 以O为圆心，OA长为半径作⊙O交BA延长线于点D ， 连接CD ．

〔1〕求证：CD是⊙O的切线；
〔2〕假设AB＝4，求图中阴影局部的面积．
21.如图，在平面直角坐标系中，矩形ABCD的边AB//x轴，AD//y轴，点A的坐标为〔2，1〕，AB=4，AD=3．

〔1〕求直线BD的解析式．
〔2〕双曲线 与折线ABC的交点为E，与折线ADC的交点为F．
①连接CE，当S△BCE=3时，求该双曲线的解析式，并求出此时点F的坐标；
②假设双曲线 与矩形ABCD各边和对角线BD的交点个数为3，请直接写出k的取值范围．

答案解析局部
一、单项选择题
1.【解析】【解答】方程移项得：x2+5x=0，
分解因式得：x〔x+5〕=0，
解得：x1=0,x2=−5，
那么他漏掉的一个根式x=0，
故答案为：B.

【分析】移项，再利用因式分解求解即可。
2.【解析】【解答】解：∵在这一组图形中，中心对称图形只有最后一个，
∴卡片上的图形是中心对称图形的概率是 ．
故答案为：D．

【分析】根据中心对称图形的定义及概率公式的计算方法求解即可。
3.【解析】【解答】解：连接BD，

∵AB是⊙O的直径，∴∠ADB=90°，
∴∠ABD=90°−∠BAD=42°，
∴∠DCA=∠ABD=42°
故答案为：B

【分析】连接BD，根据AB是⊙O的直径，求出∠ADB=90°，再利用圆周角求解即可。
4.【解析】【解答】解：①∵y=2x中k=2＞0，∴y随x的增大而增大，故本小题不符合题意；
②∵y=-2x+1中k=-2＜0，∴y随x的增大而减小，故本小题符合题意；
③∵y= 〔x＜0〕中k=2＞0，∴x＜0时，y随x的增大而减小，故本小题符合题意；
④∵y= x2+2〔x＜1〕中x＜1，∴当0＜x＜1时，y随x的增大而增大，故本小题不符合题意．
故答案为：D．

【分析】根据正比例函数、一次函数、反比例函数及二次函数的性质逐项判定即可。
5.【解析】【解答】解：连接OA、OC，

∵∠ABC=120°，
∴∠ADC=60°，
∴∠AOC=2∠ADC=120°，
那么劣弧AC的长为： ．
故答案为：B．

【分析】连接OA、OC，先求出∠ABC=120°，再利用弧长公式计算即可。
6.【解析】【解答】解：∵矩形的长为6，宽为3，
∴AB=CD=6，AD=BC=3，
∴弧BD的长=18-12=6，

故答案为：B．

【分析】根据矩形的周长等于扇形的周长求出扇形的弧长，再利用扇形的面积计算公式计算即可。
7.【解析】【解答】解：∵是剪去的两个矩形，两个矩形的面积和为20，
∴xy=10，
∴y是x的反比例函数，
∵2≤x≤10，
∴答案为A．
应选A．
【分析】先根据图形的剪切确定变化过程中的函数关系式，确定函数类型，再根据自变量及函数的取值范围确定函数的具体图象．
8.【解析】【解答】在点A中，
在点B中，
在点C中，
经比较可知：
故答案为：B
【分析】将A，B，C的横坐标代入 得出相应的 y 值，再比较大小．
9.【解析】【解答】解：∵摸球200次，其中40次摸到黑球
∴摸到黑球的概率为
∴黑球和白球的个数之和约为：10÷ =50〔个〕
∴白球的个数约为：50-10=40〔个〕
∴选C
故答案是：C.

【分析】先求出黑球的概率，再算出黑球和白球的总个数，最后相减即可。
10.【解析】【解答】解：连接BE，

设⊙O半径为r，那么OA=OD=r，OC=r-2，
∵OD⊥AB，
∴∠ACO=90°，AC=BC= AB=4，
在Rt△ACO中，由勾股定理得：r2=42+〔r-2〕2 ，
∴r=5，
∴AE=2r=10，
∵AE为⊙O的直径，
∴∠ABE=90°，
由勾股定理得：BE=6，
在Rt△ECB中，
故答案为：C．

【分析】连接BE，设⊙O半径为r，那么OA=OD=r，OC=r-2，利用勾股定理求出半径，再根据Rt△ECB，再利用勾股定理求解即可。
11.【解析】【解答】解：∵六边形ABCDEF是正六边形，
∴∠AOB=60°，
∴△OAB是等边三角形，OA=OB=AB=2，
设点G为AB与⊙O的切点，连接OG，那么OG⊥AB，

∴OG=OA∙sin60°=2×   =    ，
∴S 阴影 =S △OAB -S 扇形OMN =  ×2×  -  ．
故答案为：A．

【分析】设点G为AB与⊙O的切点，连接OG，那么OG⊥AB，先求出等边三角形OAB的面积，扇形OMN，最后作差即可。
12.【解析】【解答】解：过 作 于 ，

，
，
，
弧 的长 ，
设圆锥的底面圆的半径为 ，那么 ，解得 .
故答案为：A.
【分析】过 作 于 ，根据等腰三角形的性质得出， 进而根据含30°直角三角形的边之间的关系得出OE=OA=45，再根据弧长计算公式算出弧CD的长度，最后根据圆锥底面圆的周长等于侧面展开扇形的弧长即可列出方程，求解得出答案.
13.【解析】【解答】解：∵AB∥x轴，假设点B的坐标为〔1，3〕，
∴设点A〔a，3〕
∵S△ABC= 〔a-1〕×3=2，
∴a= ，
∴点A〔 ，3〕
∵点A在反比例函数y= 〔x＞0〕的图象上，
∴k=7，
故答案为：C.
【分析】设点A〔a，3〕，根据题意可得：a= ，即可求点A坐标，代入解析式可求k的值
二、填空题
14.【解析】【解答】解：用红1、红2、红3表示三个红球，用白1、白2表示二个的白球列表如下：

由列表知，共有20种等可能结果，其中摸出的两个球恰好一红一白的有12种结果，
∴摸出的两个球恰好一红一白的概率为 ．
故答案为： ．

【分析】列表或画出树状图求解即可。
15.【解析】【解答】解：作DH⊥x轴于H，如图，

当y=0时，-3x+3=0，解得x=1，那么A〔1，0〕，
当x=0时，y=-3x+3=3，那么B〔0，3〕，
∵四边形ABCD为正方形，
∴AB=AD，∠BAD=90°，
∴∠BAO+∠DAH=90°，
而∠BAO+∠ABO=90°，
∴∠ABO=∠DAH，
在△ABO和△DAH中
 
∴△ABO≌△DAH，
∴AH=OB=3，DH=OA=1，
∴D点坐标为〔4，1〕，
∵顶点D恰好落在双曲线y= 上，
∴a=4×1=4．
故答案是：4.

【分析】作DH⊥x轴于H，通过“AAS〞证明△ABO≌△DAH，求出点D的坐标，再带入计算即可。
16.【解析】【解答】∵⊙P的半径为2,圆心P在抛物线 上运动，
∴当⊙P与x轴相切时，假设切点为A，
∴PA=2，
∴
即 ,或 =-2
解得x= 或x=0，
∴P点的坐标为：〔 ，2〕或〔- ，2〕或〔0，-2〕

【分析】根据切线的性质：圆心到x轴的距离等于半径列出方程求解即可。
17.【解析】【解答】设△ABC的内切圆⊙M，O为△ACB的外接圆的圆心，过点M作MD⊥BC于D，ME⊥AC于E，MN⊥AB于N，

在Rt△ABC中，∵∠ACB＝90°，AC＝6，BC＝8，
∴AB＝ ＝10，
∵点O为△ABC的外心，
∴AO为外接圆半径，AO＝ AB＝5，
设⊙M的半径为r，那么MD＝ME＝r，
又∵∠MDC＝∠MEC＝∠C＝90°，
∴四边形IECD是正方形，
∴CE＝CD＝r，AE＝AN＝6﹣r，BD＝BN＝8﹣r，
∵AB＝10，
解得：r＝2，
∴MN＝r＝2，AN＝AE＝6﹣r＝6﹣2＝4，
在Rt△OMN中，∵∠MNO＝90°，ON＝AO﹣AN＝5﹣4＝1，
∴OM＝ ，
故答案为： ．
【分析】作△ABC的内切圆⊙M ， 过点M作MD⊥BC于D ， ME⊥AC于E ， MN⊥AB于N ． 先根据勾股定理求出AB＝10，得到△ABC的外接圆半径AO＝5，再证明四边形MECD是正方形，根据内心的性质和切线长定理，求出⊙M的半径r＝2，那么ON＝1，然后在Rt△OMN中，运用勾股定理即可求解．
三、解答题
18.【解析】【分析】〔1〕根据概率公式即可求解;〔2〕利用列表法,求得小贝胜与小晶胜的概率,比较即可游戏是否公平
19.【解析】【解答】解：〔3〕把B 代入y= ，得： ，
∵一次函数图象在反比例函数图象下方局部所对应的x的值，就是当 时， 的取值范围，
∴当 时， 的取值范围为：x＜-3或0＜x＜1．
故答案是：-1，x＜-3或0＜x＜1；〔4〕观察反比例函数图象可知，位于A点上和右侧及y轴左侧的图象对应的函数值均满足 ，
时，对应 的取值范围为： 或 ．

【分析】〔1〕将点A代入一次函数求出m的值，再将点A带入反比例求解即可；〔2〕根据列表、描点、作图求解即可；〔3〕联立方程求解即可；结合图象，根据函数值大的在上方求解；〔4〕结合函数图象求解即可。
20.【解析】【分析】〔1〕 连接OD， 求出∠OAD=60°，得出等边三角形OAD，求出AD=OA=AC，∠ODA=∠O=60°，求出∠ADC=∠ACD=∠OAD=30°，求出∠ODC=90°，根据切线的判定求解即可；〔2〕求出OD，根据勾股定理求出CD长，分别求出三角形ODC和扇形AOD的面积，相减即可。
21.【解析】【分析】〔1〕根据矩形的性质求出点B、D的坐标，再利用待定系数法求解即可；〔2〕①根据 S△BCE=3 求出BE的长，进而求出点E的坐标，再带入反比例函数解析式即可；②当双曲线平移经过B、D之间时，或者与BD相切时有三个交点，分别求出k的取值范围即可。