2018_2019学年临沂市兰陵县八下期末数学试卷

这是一份2018_2019学年临沂市兰陵县八下期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共14小题；共70分）
1. 下列计算错误的是
A. 2+3=5B. 2×3=6C. 18÷2=3D. 222=8

2. 如图是根据某班 40 名同学一周的体育锻炼情况绘制的统计图，该班 40 名同学一周参加体育锻炼时间的中位数，众数分别是
A. 10.5，16B. 8.5，16C. 8.5，8D. 9，8

3. 已知 x=5−12，y=5+12，则 x2+xy+y2 的值为
A. 2B. 4C. 5D. 7

4. 关于函数 y=−2x+1，下列结论正确的是
A. 图象必经过 −2,1B. y 随 x 的增大而增大
C. 图象经过第一、二、三象限D. 当 x>12 时，y<0

5. 为弘扬传统文化，某校初二年级举办传统文化进校园朗诵大赛，小明同学根据比赛中九位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是
中位数众数平均数方差
A. 中位数B. 众数C. 平均数D. 方差

6. 如图，在平行四边形 ABCD 中，DE 平分 ∠ADC，AD=8，BE=3，则平行四边形 ABCD 的周长是
A. 16B. 14C. 26D. 24

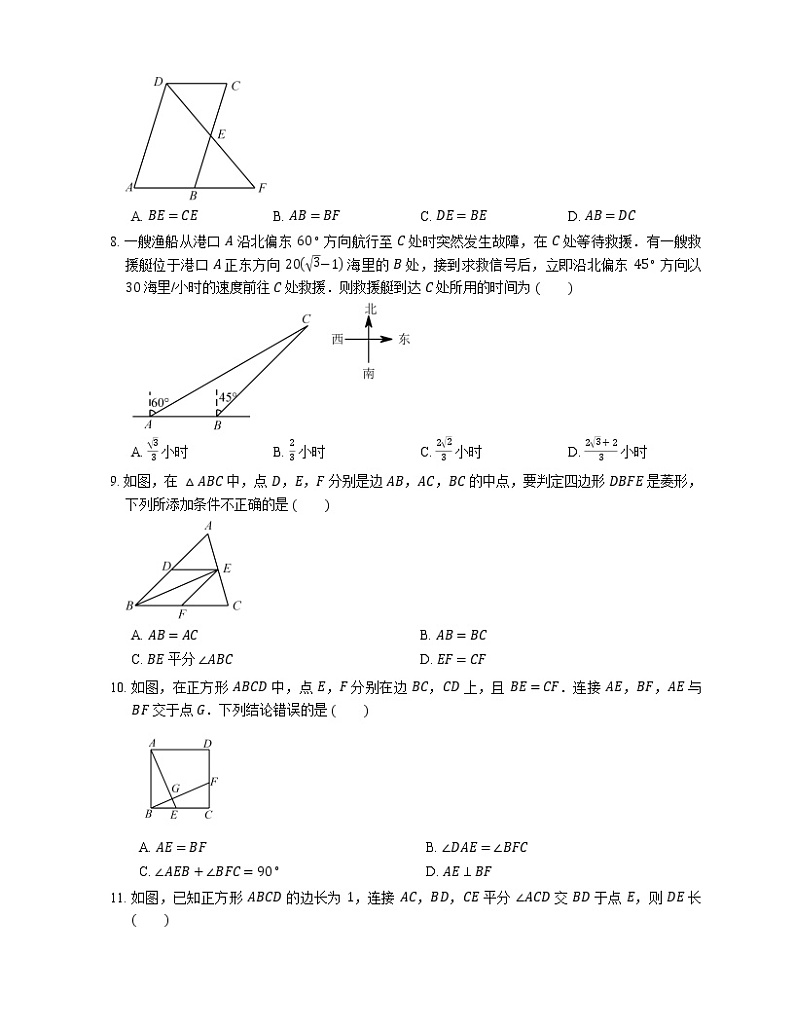
7. 如图，平行四边形 ABCD 中，E 是 BC 边的中点，连接 DE 并延长交 AB 的延长线于点 F，则在题中条件下，下列结论不能成立的是
A. BE=CEB. AB=BFC. DE=BED. AB=DC

8. 一艘渔船从港口 A 沿北偏东 60∘ 方向航行至 C 处时突然发生故障，在 C 处等待救援．有一艘救援艇位于港口 A 正东方向 203−1 海里的 B 处，接到求救信号后，立即沿北偏东 45∘ 方向以 30 海里/小时的速度前往 C 处救援．则救援艇到达 C 处所用的时间为
A. 33 小时B. 23 小时C. 223 小时D. 23+23 小时

9. 如图，在 △ABC 中，点 D，E，F 分别是边 AB，AC，BC 的中点，要判定四边形 DBFE 是菱形，下列所添加条件不正确的是
A. AB=ACB. AB=BC
C. BE 平分 ∠ABCD. EF=CF

10. 如图，在正方形 ABCD 中，点 E，F 分别在边 BC，CD 上，且 BE=CF．连接 AE，BF，AE 与 BF 交于点 G．下列结论错误的是
A. AE=BFB. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90∘D. AE⊥BF

11. 如图，已知正方形 ABCD 的边长为 1，连接 AC，BD，CE 平分 ∠ACD 交 BD 于点 E，则 DE 长
A. 2−1B. 22C. 1D. 1−22

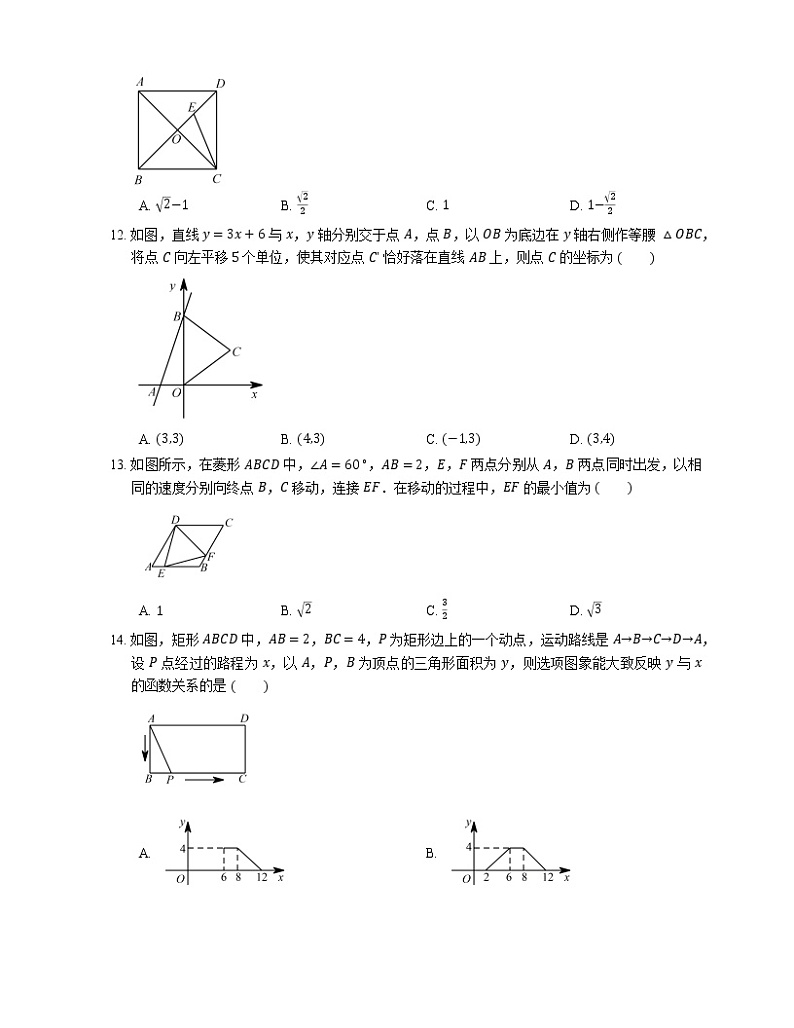
12. 如图，直线 y=3x+6 与 x，y 轴分别交于点 A，点 B，以 OB 为底边在 y 轴右侧作等腰 △OBC，将点 C 向左平移 5 个单位，使其对应点 Cʹ 恰好落在直线 AB 上，则点 C 的坐标为
A. 3,3B. 4,3C. −1,3D. 3,4

13. 如图所示，在菱形 ABCD 中，∠A=60∘，AB=2，E，F 两点分别从 A，B 两点同时出发，以相同的速度分别向终点 B，C 移动，连接 EF．在移动的过程中，EF 的最小值为
A. 1B. 2C. 32D. 3

14. 如图，矩形 ABCD 中，AB=2，BC=4，P 为矩形边上的一个动点，运动路线是 A→B→C→D→A，设 P 点经过的路程为 x，以 A，P，B 为顶点的三角形面积为 y，则选项图象能大致反映 y 与 x 的函数关系的是
A. B.
C. D.

二、填空题（共5小题；共25分）
15. 计算：1+22×1−22= ．

16. 如图，矩形 ABCD 中，AB=8，BC=4，将矩形沿 AC 折叠，点 D 落在点 Dʹ 处，则重叠部分 △AFC 的面积为 ．

17. 某校八年级甲、乙两班举行电脑汉字输入比赛，两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如表：
班级参加人数平均字数中位数方差甲55135149191乙55135151110
有一位同学根据上表得出如下结论：
①甲、乙两班学生的平均水平相同；
②乙班优秀的人数比甲班优秀的人数多（每分钟输入汉字达 150 个以上为优秀）；
③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大．
上述结论正确的是 （填序号）．

18. 在正方形 ABCD 中，E 是 BC 边延长线上的一点，且 CE=BD，则 ∠AEC= ．

19. 张师傅驾车从甲地到乙地匀速行驶，已知行驶中油箱剩余油量 y（升）与行驶时间 t（小时）之间的关系用如图的线段 AB 表示，根据这个图象求出 y 与 t 之间的函数关系式为 y=−7.5t+25，那么函数 y=−7.5t+25 中的常数 −7.5 表示的实际意义是 ．

三、解答题（共5小题；共65分）
20. 如图，甲、乙两人以相同路线前往离学校 12 千米的地方参加植树活动．分析甲、乙两人前往目的地所行驶的路程 S（千米）随时间 t（分钟）变化的函数图象，解决下列问题：
（1）求出甲、乙两人所行驶的路程 S甲，S乙 与 t 之间的关系式；
（2）甲行驶 10 分钟后，甲、乙两人相距多少千米?

21. 王先生准备采购一批（大于 100 条）某种品牌的跳绳，采购跳绳有在实体店和在网店购买两种方式，通过洽谈，获得了以下信息：
购买方式标价元条优惠条件实体店40全部按标价的8折出售网店40购买100或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售免邮寄费
（1）请分别写出王先生在实体店、网店购买跳绳所需的资金 y1，y2 元与购买的跳绳数 xx>100 条之间的函数关系式；
（2）王先生选取哪种方式购买跳绳省钱?

22. 如图，在平行四边形 ABCD 中，∠BAD 的平分线与 BC 的延长线交于点 E，与 DC 交于点 F．
（1）求证：CD=BE；
（2）若 AB=4，点 F 为 DC 的中点，DG⊥AE，垂足为 G，且 DG=1，求 AE 的长．

23. 在菱形 ABCD 中，∠ABC=60∘，E 是对角线 AC 上任意一点，F 是线段 BC 延长线上一点，且 CF=AE，连接 BE，EF．
（1）如图 1，当 E 是线段 AC 的中点时，求证：BE=EF．
（2）如图 2，当点 E 不是线段 AC 的中点，其它条件不变时，请你判断（1）中的结论是否成立?若成立，请证明；若不成立，说明理由．

24. 如图，在平面直角坐标系中，过点 B6,0 的直线 AB 与直线 OA 相交于点 A4,2，动点 M 在 y 轴上运动．
（1）求直线 AB 的函数解析式；
（2）动点 M 在 y 轴上运动，使 MA+MB 的值最小，求点 M 的坐标；
（3）在 y 轴的负半轴上是否存在点 M，使 △ABM 是以 AB 为直角边的直角三角形?如果存在，求出点 M 的坐标；如果不存在，说明理由．
答案
第一部分
1. A【解析】A、 2，3 不是同类二次根式，不能合并，此选项错误；
B、 2×3=2×3=6，此选项正确；
C、 18÷2=18÷2=9=3，此选项正确；
D、 222=8，此选项正确．
2. D
3. B【解析】∵x=5−12，y=5+12，
∴x+y=5，xy=1 .
∴x2+xy+y2=x+y2−xy=5−1=4 .
4. D【解析】根据一次函数的性质，依次分析可得，
A、 x=−2 时，y=−2×−2+1=5，故图象必经过 −2,5，故错误，
B、 k<0，则 y 随 x 的增大而减小，故错误，
C、 k=−2<0，b=1>0，则图象经过第一、二、四象限，故错误，
D、当 x>12 时，y<0，正确．
5. A
【解析】如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是中位数．
6. C
7. C【解析】∵E 是 BC 边的中点，
∴BE=CE，
∵ 四边形 ABCD 是平行四边形，
∴AB=DC，AB∥CD，
∴∠C=∠EBF，
在 △BFE 和 △CDE 中，
∠EBF=∠C,BE=CE,∠BEF=∠CED,
∴△BFE≌△CDE，
∴BF=CD，DE=EF．
∴AB=BF．
∵BE=EF 无法证明，
∴DE=BE 结论不成立．
8. C【解析】如图，过点 C 作 CD⊥AB，交 AB 的延长线于点 D．
由题意，得 ∠CAD=90∘−60∘=30∘，设 CD=x 海里．
在 Rt△CAD 中，
∵∠CAD=30∘，
∴AC=2CD=2x 海里，AD=3CD=3x 海里．
在 Rt△CBD 中，
∵∠CBD=90∘−45∘=45∘，
∴BD=CD=x 海里．
∵AD−BD=AB，
∴3x−x=203−1，解得 x=20，
∴BC=2CD=202 海里，
∵ 救援艇的速度为 30 海里/小时，
∴ 救援艇到达 C 处所用的时间为 20230=223（小时）．
9. A【解析】当 AB=BC 时，四边形 DBFE 是菱形；
理由：∵ 点 D，E，F 分别是边 AB，AC，BC 的中点，
∴DE∥BC，EF∥AB，DE=12BC，EF=12AB，
∴ 四边形 DBFE 是平行四边形，
∵AB=BC，
∴DE=EF，
∴ 四边形 DBFE 是菱形．
故B正确，不符合题意，
当 BE 平分 ∠ABC 时，可证 BD=DE，可得四边形 DBFE 是菱形，
当 EF=FC，可证 EF=BF，可得四边形 DBFE 是菱形，
故C、D不符合题意．
10. C
11. A【解析】如图，过 E 作 EF⊥DC 于 F，
∵ 四边形 ABCD 是正方形，
∴AC⊥BD，
∵CE 平分 ∠ACD 交 BD 于点 E，
∴EO=EF，
∵ 正方形 ABCD 的边长为 1，
∴AC=2，
∴CO=12AC=22，
∴CF=CO=22，
∵EF∥BC，
∴∠DEF=∠DBC=∠BDC，
∴EF=DF=DC−CF=1−22，
∴DE=EF2+DF2=2−1．
12. B
13. D
14. B
第二部分
15. 1
16. 10
【解析】易证 △AFDʹ≌△CFB，
∴DʹF=BF，
设 DʹF=x，则 AF=8−x，
在 Rt△AFDʹ 中，8−x2=x2+42，
解得：x=3，
∴AF=AB−FB=8−3=5，
∴S△AFC=12⋅AF⋅BC=10．
17. ①②③
【解析】① ∵ 甲乙两班学生比赛成绩的平均数相同，
∴ 甲、乙两班学生的平均水平相同，说法正确；
② ∵ 乙班学生比赛成绩的中位数比甲班的大且大于 150，
∴ 乙班优秀的人数比甲班优秀的人数多（每分钟输入汉字达 150 个以上为优秀），说法正确；
③ ∵ 甲班学生比赛成绩的方差比乙班的大，
∴ 甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大，说法正确．
18. 22.5∘
19. 表示每小时耗油 7.5 升
【解析】函数 y=−7.5t+25 中的常数 −7.5 表示的实际意义是表示每小时耗油 7.5 升．
第三部分
20. （1） 由图象设甲的解析式为：S甲=kt，代入点 24,12，解得：k=0.5；
所以甲的解析式为：S甲=0.5t；
同理可设乙的解析式为：S乙=mt+b，代入点 6,0，18,12，
可得：6m+b=0,18m+b=12，
解得：m=1,b=−6，
所以乙的解析式为 S乙=t−6；
（2） 当 t=10 时，S甲=0.5×10=5（千米），S乙=10−6=4（千米），5−4=1（千米），
答：甲行驶 10 分钟后，甲、乙两人相距 1 千米．
21. （1） 由题意可得，
王先生在实体店购买跳绳所需的资金 y1（元）与购买的跳绳数 x（条）之间的函数关系式为：y1=40x×0.8=32x；
王先生在网店购买跳绳所需的资金 y2（元）与购买的跳绳数 x（条）之间的函数关系式为：y2=40×100+x−100×40×0.7=28x+1200．
（2） 当 y1>y2 时，32x>28x+1200，解得 x>300；
当 y1=y2 时，32x=28x+1200，解得 x=300；
当 y128x+1200，解得 x<300；
∴ 当 100300 时，在网店购买省钱．
22. （1） ∵AE 为 ∠BAD 的平分线，
∴∠DAE=∠BAE．
∵ 四边形 ABCD 是平行四边形，
∴AD∥BC，CD=AB．
∴∠DAE=∠E．
∴∠BAE=∠E．
∴AB=BE．
∴CD=BE．
（2） ∵ 四边形 ABCD 是平行四边形，
∴CD∥AB，
∴∠BAF=∠DFA．
又 ∠DAF=∠FAB，
∴∠DAF=∠DFA．
∴DA=DF．
∵F 为 DC 的中点，AB=4，
∴DF=CF=DA=2．
∵DG⊥AE，DG=1，
∴AG=GF．
∴AG=3．
∴AF=2AG=23．
∵AD∥BC，
∴∠ADF=∠ECF．
在 △ADF 和 △ECF 中，
∠DAF=∠E,∠ADF=∠ECF,DF=CF,
∴△ADF≌△ECF．
∴AF=EF，
∴AE=2AF=43．
23. （1） ∵ 四边形 ABCD 是菱形，
∴AB=BC，
∵∠ABC=60∘，
∴△ABC 是等边三角形，
∴∠BCA=60∘，
∵E 是线段 AC 的中点，
∴∠CBE=∠ABE=30∘，AE=CE，
∵CF=AE，
∴CE=CF，
∴∠F=∠CEF=12∠BCA=30∘，
∴∠CBE=∠F=30∘，
∴BE=EF；
（2） 结论成立；理由如下：
过点 E 作 EG∥BC 交 AB 于点 G，如图所示：
∵ 四边形 ABCD 为菱形，
∴AB=BC，
∵∠ABC=60∘，
∴△ABC 是等边三角形，
∴AB=AC，∠ACB=60∘，
∴∠ECF=120∘，
∵EG∥BC，
∴∠AGE=∠ABC=60∘，
∵∠BAC=60∘，
∴△AGE 是等边三角形，
∴AG=AE=GE，
∴BG=CE，∠BGE=120∘=∠ECF，
∵CF=AE，
∴GE=CF，
在 △BGE 和 △ECF 中，
BG=CE,∠BGE=∠ECF,GE=CF.
∴△BGE≌△ECF，
∴BE=EF．
24. （1） 设直线 AB 的解析式为 y=kx+b，
∵A4,2，B6,0，
∴6k+b=0,4k+b=2,
∴k=−1,b=6,
∴ 直线 AB 的解析式为 y=−x+6．
（2） 如图 1，作点 B6,0 关于 y 轴的对称点 Bʹ，
∴Bʹ−6,0，
连接 ABʹ 交 y 轴于 M，此时 MA+MB 最小，
设直线 ABʹ 的解析式为 y=mx+n，
∵A4,2，Bʹ−6,0，
∴4m+n=2,−6m+n=0,
∴m=15,n=65,
∴ 直线 ABʹ 的解析式为 y=15x+65，
令 x=0，
∴y=65，
∴M0,65．
（3） 如图 2，△ABM 是以 AB 为直角边的直角三角形，
①当 ∠MAB=90∘ 时，MA⊥AB，
∵ 设直线 AB 的解析式为 y=−x+6，
∴ 设直线 AM 的解析式为 y=x+bʹ，
∵A4,2，
∴4+bʹ=2，
∴bʹ=−2，
∴M0,−2，
②当 ∠MʹBA=90∘ 时，MʹB⊥AB，
∴ 设直线 BMʹ 的解析式为 y=x+nʹ，
∵B6,0，
∴6+nʹ=0，
∴nʹ=−6，
∴Mʹ0,−6．
即：满足条件的点 M 的坐标为 0,−2 或 0,−6．