2019年江苏省苏州市高新区中考一模数学试卷

这是一份2019年江苏省苏州市高新区中考一模数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 2−1 等于
A. 12B. 2C. −12D. −2

2. 绝对值大于 3 且小于 6 的所有整数的和是
A. 0B. 9C. 18D. 27

3. 下列事件是必然事件的是
A. 打开电视机，正在播放动画片
B. 在一只装有 5 个红球的袋中摸出 1 球，一定是红球
C. 某彩票中奖率是 1%，买 100 张一定会中奖
D. 2018 年世界杯德国队一定能夺得冠军

4. 点 M1,−2 关于原点对称的点的坐标是
A. −1,−2B. 1,2C. −1,2D. −2,1

5. 关于 x 的一元二次方程 x2−2m−2x+m2=0 有两个不相等的实数根，则 m 的取值范围为
A. m>1B. m<1C. m>−1D. m<−1

6. 如果小磊将镖随意投中如图所示的正方形木板假设投中每个小正方形是等可能的，那么镖落在阴影部分的概率为
A. 16B. 12C. 13D. 14

7. 反比例函数 y=6x 图象上有三个点 −2,y1，−1,y2，1,y3，则 y1，y2，y3 的大小关系是
A. y1
8. 关于 x 的分式方程 2x−ax+1=1 的解为正数，则字母 a 的取值范围为
A. a≥−1B. a>−1C. a≤−1D. a<−1

9. 已知二次函数y=a(x−2)2+c，当x=x1时，函数值为y1；当x=x2时，函数值为y2，若∣x1−2∣>∣x2−2∣，则下列表达式正确的是( )
A. y1+y2>0B. y1−y2>0C. a(y1−y2)>0D. a(y1+y2)>0

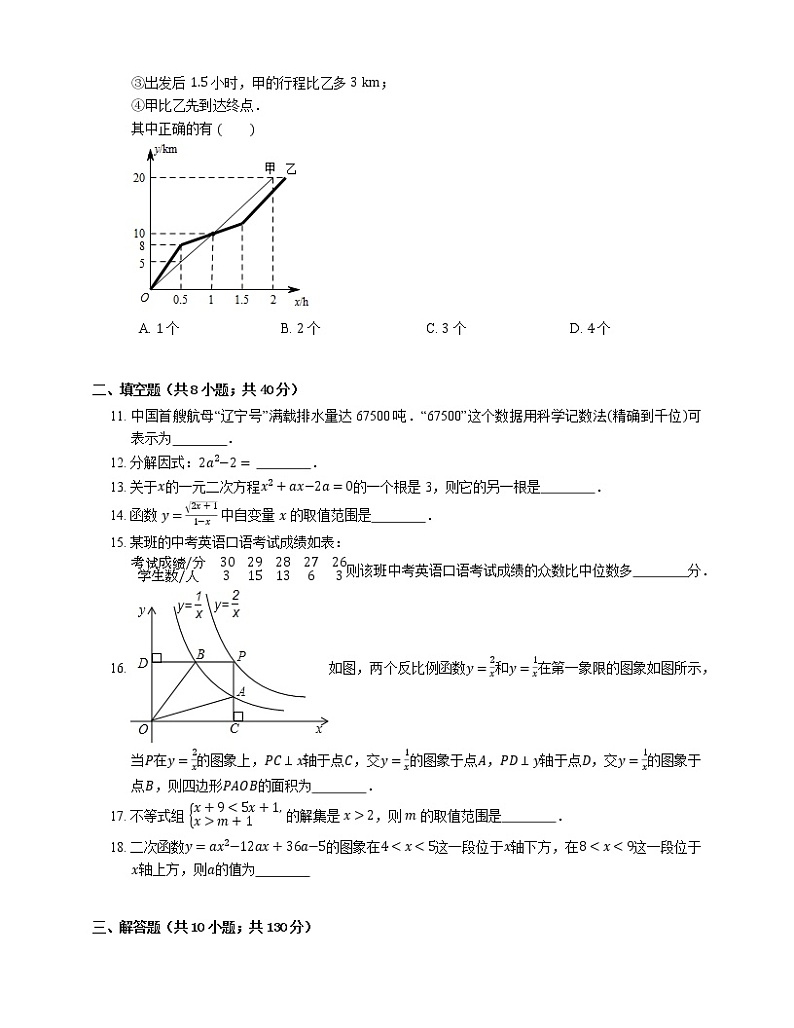
10. 在 20 km 越野赛中，甲乙两选手的行程 y（单位：km）随时间 x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：
①两人相遇前，甲的速度小于乙的速度；
②出发后 1 小时，两人行程均为 10 km；
③出发后 1.5 小时，甲的行程比乙多 3 km；
④甲比乙先到达终点．
其中正确的有
A. 1 个B. 2 个C. 3 个D. 4 个

二、填空题（共8小题；共40分）
11. 中国首艘航母“辽宁号”满载排水量达67500吨．“67500”这个数据用科学记数法精确到千位可表示为 ．

12. 分解因式：2a2−2= ．

13. 关于x的一元二次方程x2+ax−2a=0的一个根是3，则它的另一根是 ．

14. 函数 y=2x+11−x 中自变量 x 的取值范围是 ．

15. 某班的中考英语口语考试成绩如表：
考试成绩/分3029282726学生数/人3151363则该班中考英语口语考试成绩的众数比中位数多 分．

16. 如图，两个反比例函数y=2x和y=1x在第一象限的图象如图所示，当P在y=2x的图象上，PC⊥x轴于点C，交y=1x的图象于点A，PD⊥y轴于点D，交y=1x的图象于点B，则四边形PAOB的面积为 ．

17. 不等式组 x+9<5x+1,x>m+1 的解集是 x>2，则 m 的取值范围是 ．

18. 二次函数y=ax2−12ax+36a−5的图象在4
三、解答题（共10小题；共130分）
19. 计算：3−10+∣−3∣−4．

20. 解不等式组：x+3≥2,2x+4>4x+2.

21. 先化简，再求值：1−1a÷a2−2a+1a，其中 a=2+1．

22. 已知多项式 A=2x2+2xy+my−8，B=−nx2+xy+y+7，A−2B 中不含有 x2 项和 y 项，求 m+n 的值．

23. 某校为了了解初三年级 1000 名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A:39.5∼46.5；B:46.5∼53.5；C:53.5∼60.5；D:60.5∼67.5；E:67.5∼74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．
解答下列问题：
（1）这次抽样调查的样本容量是 ，并补全频数分布直方图；
（2）C 组学生的频率为 ，在扇形统计图中 D 组的圆心角是 度；
（3）请你估计该校初三年级体重超过 60 kg 的学生大约有多少名?

24. 如图，一次函数 y=x+m 与反比例函数 y=kx 的图象相交于 A2,1，B 两点．
（1）求 m 及 k 的值；
（2）不解关于 x，y 的方程组 y=x+m,y=kx, 直接写出 B 点的坐标；
（3）看图象直接写出，x+m>kx 时，自变量 x 的取值范围．

25. 在甲、乙两个不透明的布袋，甲袋中装有 3 个完全相同的小球，分别标有数字 0，1，2；乙袋中装有 3 个完全相同的小球，分别标有数字 −1，−2，0；现从甲袋中随机抽取一个小球，记录标有的数字为 x，再从乙袋中随机抽取一个小球，记录标有的数字为 y，确定点 M 坐标为 x,y．
（1）用树状图或列表法列举点 M 所有可能的坐标；
（2）求点 Mx,y 在函数 y=−x+1 的图象上的概率．

26. 为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是 40 元．超市规定每盒售价不得少于 45 元．根据以往销售经验发现；当售价定为每盒 45 元时，每天可以卖出 700 盒，每盒售价每提高 1 元，每天要少卖出 20 盒．
（1）试求出每天的销售量 y（盒）与每盒售价 x（元）之间的函数关系式；
（2）当每盒售价定为多少元时，每天销售的利润 P（元）最大?最大利润是多少?
（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于 58 元．如果超市想要每天获得不低于 6000 元的利润，那么超市每天至少销售粽子多少盒?

27. 如图在平面直角坐标系中，四边形 OABC 是菱形，点 C 的坐标为 3,4，平行于对角线 AC 的直线 m 从原点 O 出发，沿 x 轴正方向以每秒 1 个单位长度的速度运动，设直线 m 与菱形 OABC 的两边分别交于点 M，N，直线 m 运动的时间为 t（秒）．
（1）求点 B 的坐标；
（2）当 MN=12AC 时，求 t 的值；
（3）设 △OMN 的面积为 S，求 S 与 t 的函数表达式，并确定 S 的最大值．

28. 如图，在平面直角坐标系中，抛物线 y=ax2−2ax−3aa>0 与 x 轴交于 A，B 两点（点 A 在点 B 左侧），经过点 A 的直线 l：y=kx+b 与轴 y 交于点 C，与抛物线的另一个交点为 D，且 CD=4AC．
（1）直接写出点 A 的坐标，并用含 a 的式子表示直线 l 的函数表达式（其中 k，b 用含 a 的式子表示）．
（2）点 E 为直线 l 下方抛物线上一点，当 △ADE 的面积的最大值为 254 时，求抛物线的函数表达式；
（3）设点 P 是抛物线对称轴上的一点，点 Q 在抛物线上，以点 A，D，P，Q 为顶点的四边形能否为矩形?若能，求出点 P 的坐标；若不能，请说明理由．
答案
第一部分
1. A【解析】原式=12．
2. A【解析】绝对值大于 3 小于 6 的所有整数是 ±4，±5．
4+−4+5+−5=0+0=0．
故选：A．
3. B【解析】A．打开电视机，正在播放动画片是随机事件；
B．在一只装有 5 个红球的袋中摸出 1 球，一定是红球是必然事件；
C．某彩票中奖率是 1%，买 100 张一定会中奖是随机事件；
D．2018 年世界杯德国队一定能夺得冠军是随机事件．
4. C【解析】点 M1,−2 关于原点对称的点的坐标是 −1,2．
5. B
【解析】因为关于 x 的一元二次方程 x2−2m−2x+m2=0 有两个不相等的实数根．
所以 Δ=4m−22−4m2>0，
解之得 m<1．
故选：B．
6. A【解析】【分析】看阴影部分的面积占正方形木板面积的多少即可．
【解析】解：阴影部分的面积为2+4=6，
∴镖落在阴影部分的概率为636=16．
故选：A．
【点评】此题考查几何概率的求法；用到的知识点为：概率=相应的面积与总面积之比．
7. C【解析】∵k>0，函数图象如图，
∴ 图象在第一、三象限，在每个象限内，y 随 x 的增大而减小，
∵−2<−1<1，
∴y28. B【解析】分式方程的解 x=a+1，x>0 且 x≠−1，所以 a>−1．
9. C【解析】【分析】分a>0和a<0两种情况根据二次函数的对称性确定出y1与y2的大小关系，然后对各选项分析判断即可得解．
【解析】解：①a>0时，二次函数图象开口向上，
∵∣x1−2∣>∣x2−2∣，
∴y1>y2，
无法确定y1+y2的正负情况，
a(y1−y2)>0，
②a<0时，二次函数图象开口向下，
∵∣x1−2∣>∣x2−2∣，
∴y1无法确定y1+y2的正负情况，
a(y1−y2)>0，
综上所述，表达式正确的是a(y1−y2)>0．
故选：C．
【点评】本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的对称性，难点在于根据二次项系数a的正负情况分情况讨论．
10. C
【解析】由图象可知两人相遇前，前半小时甲的速度大于乙的速度，后半小时甲的速度小于乙的速度，可得①错误；
出发一小时后甲乙两人相遇，距离相等，均为 10 km，可得②正确；
由 1,10 可得代表甲的图象所在直线的解析式为 y=10x，
由 0.5,8 、 1,10 可得代表乙在 0.5−1.5 之间的图象所在直线的解析式为 y=4x+6，
将 x=1.5 分别代入两个函数解析式中可得此时甲的行程为 15，乙的行程为 12，可得③正确；
由图象可得甲 2 小时到达终点，乙到达终点的时间大于 2 小时，可得④正确．
第二部分
11. 6.8×104
【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤∣a∣<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>10时，n是正数；当原数的绝对值<1时，n是负数．
确定a×10n1≤∣a∣<10，n为整数中n的值是易错点，由于67500有5位，所以可以确定n=5−1=4．
【解析】解：将67500这个数据精确到千位，用科学记数法表示为：6.8×104．
故答案是：6.8×104．
【点评】此题主要考查了科学记数法与有效数字，把一个数M记成a×10n1≤∣a∣<10，n为整数的形式，这种记数的方法叫做科学记数法．
规律：(1)当∣a∣≥1时，n的值为a的整数位数减1；
(2)当∣a∣<1时，n的值是第一个不是0的数字前0的个数，包括整数位上的0．
注意本题精确到千位．
12. 2a+1a−1
【解析】2a2−2=2a2−1=2a+1a−1．
13. 6
【解析】【分析】把x=3代入方程x2+ax−2a=0得出9+3a−2a=0，求出a=−9，方程为x2−9x+18=0，设方程的另一个根为b，得出b+3=9，求出即可．
【解析】解：把x=3代入方程x2+ax−2a=0得：9+3a−2a=0，
解得：a=−9，
即方程为x2−9x+18=0，
设方程的另一个根为b，
则b+3=9，
解得：b=6，
故答案为：6．
【点评】本题考查了一元二次方程的解，根与系数的关系的应用，解此题的关键是求出a的值和得出b+3=9．
14. x≥−12 且 x≠1
【解析】根据题意得，2x+1≥0 且 1−x≠0，
解得 x≥−12 且 x≠1．
15. 1
【解析】【分析】众数是一组数据中出现次数最多的数据，注意众数可以不只一个；找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．
【解析】解：这组数出现次数最多的是29；
∴这组数的众数是29．
∵共40人，
∴中位数应是第20和第21人的平均数，
位于最中间的数是28，28，
∴这组数的中位数是28．
∴该班中考英语口语考试成绩的众数比中位数多29−28=1分，
故答案为：1．
【点评】本题属于基础题，考查了确定一组数据的中位数和众数的能力．要明确定义，一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．
16. 1
【解析】【分析】此题所求的四边形PAOB的面积可由分割法，S四边形PAOB=S□PCOD−S△DBO−S△ACO．
【解析】解：由于P点在y=2x上，则S□PCOD=2，A、B两点在y=1x上，
则S△DBO=S△ACO=12×1=12．
∴S四边形PAOB=S□PCOD−S△DBO−S△ACO=2−12−12=1．
∴四边形PAOB的面积为1．
故答案为：1．
【点评】本题考查了反比例函数k的几何意义，∣k∣可以表示为图象上一点到两坐标轴作垂线所围成的矩形的面积．
17. m≤1
【解析】x+9<5x+1, ⋯⋯①x>m+1, ⋯⋯②
由 ① 得：x>2，
由 ② 得：x>m+1，
因为不等式组 x+9<5x+1,x>m+1 的解集是 x>2，
所以 2≥m+1，
所以 m≤1．
18. 54
【解析】【分析】先求出抛物线的对称轴为直线x=6，利用抛物线的对称性得到x=4和x=8对应的函数值相等，则可判断抛物线与x轴的交点坐标为4，0，8，0，然后把4，0代入解析式可求出a的值．
【解析】解：∵抛物线的对称轴为直线x=−−12a2a=6，
∴x=4和x=8对应的函数值相等，
∵在4∴抛物线与x轴的交点坐标为4，0，8，0，
把4，0代入y=ax2−12ax+36a−5得16a−48a+36a−5=0，解得a=54．
故答案为54．
【点评】本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+ca，b，c是常数，a≠0与x轴的交点坐标问题转化解．关于x的一元二次方程即可求得交点横坐标．
第三部分
19. 原式=1+3−2=2．
20.
x+3≥2, ⋯⋯①2x+4>4x+2. ⋯⋯②
因为解不等式 ① 得：
x≥−1.
解不等式 ② 得：
x<3.
所以不等式组的解集为
−1≤x<3.
21. 原式=a−1a÷a−12a=a−1a⋅aa−12=1a−1,
当 a=2+1 时，
原式=12+1−1=12=22.
22. ∵A=2x2+2xy+my−8，B=−nx2+xy+y+7，
∴A−2B=2x2+2xy+my−8+2nx2−2xy−2y−14=2+2nx2+m−2y−22,
由结果不含 x2 项和 y 项，得到 2+2n=0，m−2=0，
解得：m=2，n=−1，
则 m+n=1．
23. （1） 50；B 组的频数 =50−4−16−10−8=12，
补全频数分布直方图，如图：
【解析】这次抽样调查的样本容量是 4÷8%=50．
（2） 0.32；72
【解析】C 组学生的频率是 0.32；D 组的圆心角 =1050×360∘=72∘．
（3） 样本中体重超过 60 kg 的学生是 10+8=18 人，
该校初三年级体重超过 60 kg 的学生 =1850×100%×1000=360 人．
24. （1） 将 m，k 分别代入一次函数 y=x+m 与反比例函数 y=kx，
可得，1=2+m，1=k2，
解得：m=−1，k=2．
（2） 因为 A，B 两点关于直线 x=−y 对称，
所以 B 点的坐标为 −1,−2．
（3） −12．
25. （1） 列表如表：
x
y012−10,−11,−12,−1−20,−21,−22,−200,01,02,0
共有 9 种等可能的结果数．
（2） 满足点 x,y 落在函数 y=−x+1 的图象上的结果有 2 个，即 2,−1，1,0，
所以点 Mx,y 在函数 y=−x+1 的图象上的概率 =29．
26. （1） 由题意得，y=700−20x−45=−20x+160045≤x≤80．
（2） P=x−40−20x+1600=−20x2+2400x−64000=−20x−602+8000.
∵x≥45，a=−20<0，
∴ 当 x=60 时，P最大值=8000 元，
即当每盒售价定为 60 元时，每天销售的利润 P（元）最大，最大利润是 8000 元．
（3） 由题意，得 −20x−602+8000=6000，解得 x1=50，x2=70．
∵ 抛物线 P=−20x−602+8000 的开口向下，
∴ 当 50≤x≤70 时，每天销售粽子的利润不低于 6000 元的利润．
又 ∵x≤58，
∴50≤x≤58．
∵ 在 y=−20x+1600 中，k=−20<0，
∴y 随 x 的增大而减小，
∴ 当 x=58 时，y最小值=−20×58+1600=440，
即超市每天至少销售粽子 440 盒．
27. （1） 过点 C 作 CH⊥OA 于 H，如图 1 所示：
∵C3,4，
∴CH=4，OH=3，
∴OC=42+32=5，
∵ 四边形 OABC 是菱形，
∴CB=OC=5，5+3=8，
∴ 点 B 的坐标为 8,4．
（2） 分两种情况：
①当 0≤t≤5 时，如图 2 所示：
∵ 四边形 OABC 是菱形，
∴OA=AB=BC=OC=5，OC∥AB．
∵MN∥AC，
∴△OMN∽△OAC，
∴MNAC=OMOA．
∵MN=12AC，
∴OM=12OA
∴OM=52，
∴t=52．
②当 5≤t≤10 时，如图 3 所示：
设直线 MN 与 OA 交于点 E，同①可得 AM=52．
∵OC∥AB，MN∥AC，
∴∠COA=∠MAE，∠CAO=∠MEA，
∴△AEM∽△OAC．
∴AEOA=AMOC．
∵OC=OA，
∴AM=AE，
∴OE=152，
∴t=152．
综上所述：t=52 或 t=152．
（3） 分两种情况：
①当 0≤t<5 时（如图 1），S△OAC=12OA⋅CH=10．
∵△OMN∽△OAC，
∴S△OMNS△OAC=OMOA2，即 S△OMN10=t52，
∴S=25t20≤t<5；
②当 5≤t≤10 时，过点 M 作 MT⊥x 轴于 T，如图 4 所示：
由 △BMN∽△AME 可知，MT=45t−5，
∴S△OMN=S△ONE−S△OME=−25t−52+10．
综上所述：S=25t2,0≤t<5−25t−52+10,5≤t≤10．
∴ 当 t=5 时，S最大值=10．
28. （1） A−1,0．
如图 1，作 DF⊥x 轴于 F，
所以 DF∥OC，
所以 OFOA=CDAC，
因为 CD=4AC，
所以 OFOA=CDAC=4，
因为 OA=1，
所以 OF=4，
所以 D 点的横坐标为 4，
代入 y=ax2−2ax−3a 得，y=5a，
所以 D4,5a，
把 A，D 坐标代入 y=kx+b 得 −k+b=0,4k+b=5a,
解得 k=a,b=a,
所以直线 l 的函数表达式为 y=ax+a．
【解析】令 y=0，则 ax2−2ax−3a=0，
解得 x1=−1，x2=3，
因为点 A 在点 B 的左侧，
所以 A−1,0．
（2） 如图 2，过点 E 作 EH∥y 轴，交直线 l 于点 H，
设 Ex,ax2−2ax−3a，则 Hx,ax+a．
所以 HE=ax+a−ax2−2ax−3a=−ax2+3ax+4a，
所以 S△ADE=S△AEH+S△DEH=52−ax2+3ax+4a=−52ax−322+1258a．
所以 △ADE 的面积的最大值为 1258a，
所以 1258a=254，
解得：a=25．
所以抛物线的函数表达式为 y=25x2−45x−65．
（3） 已知 A−1,0，D4,5a
所以 y=ax2−2ax−3a．
所以抛物线的对称轴为 x=1，
设 P1,m，
①若 AD 为矩形的边，且点 Q 在对称轴左侧时，则 AD∥PQ，且 AD=PQ，
则 Q−4,21a，m=21a+5a=26a，则 P1,26a，
因为四边形 ADPQ 为矩形，
所以 ∠ADP=90∘，
所以 AD2+PD2=AP2，
所以 52+5a2+1−42+26a−5a2=−1−12+26a2，
即 a2=17，
因为 a>0，
所以 a=77，
所以 P11,2677，
②若点 Q 在对称轴右侧时，则 AD∥PQ，且 AD=PQ，
则点 Q 的横坐标为 6，
此时 QD 显然不垂直于 AD，不符合题意，舍去；
③若 AD 是矩形的一条对角线，则 AD 与 PQ 互相平分且相等．
所以 xD+xA=xP+xQ，yD+yA=yP+yQ，
所以 xQ=2，
所以 Q2,−3a．
所以 yP=8a．
所以 P1,8a．
因为四边形 APDQ 为矩形，
所以 ∠APD=90∘，
所以 AP2+PD2=AD2，
所以 −1−12+8a2+1−42+8a−5a2=52+5a2，
即 a2=14，
因为 a>0，
所以 a=12．
所以 P21,4．
综上所述，以点 A，D，P，Q 为顶点的四边形能成为矩形，点 P 的坐标为 1,2677 或 1,4．