2019年北京市海淀区中考数学一模试卷

这是一份2019年北京市海淀区中考数学一模试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 如图是圆规示意图，张开的两脚所形成的角大约是
A. 90∘B. 60∘C. 45∘D. 30∘

2. 若 x−1 在实数范围内有意义，则实数 x 的取值范围是
A. x≥1B. x≤1C. x<1D. x≠1

3. 实数 a，b，c 在数轴上的对应点的位置如图所示，若 a=b，则下列结论中错误的是
A. a+b>0B. a+c>0C. b+c>0D. ac<0

4. 若正多边形的内角和是 540∘，则该正多边形的一个外角为
A. 45∘B. 60∘C. 72∘D. 90∘

5. 2019 年 2 月，美国宇航局（NASA）的卫星监测数据显示地球正在变绿，分析发现是中国和印度的行动主导了地球变绿．尽管中国和印度的土地面积加起来只占全球的 9%，但过去 20 年间地球三分之一的新增植被是两国贡献的，面积相当于一个亚马逊雨林．已知亚马逊雨林的面积为 6560000 km2，则过去 20 年间地球新增植被的面积约为
A. 6.56×106 km2B. 6.56×107 km2C. 2×107 km2D. 2×108 km2

6. 如果 a2−ab−1=0，那么代数式 a2a−b⋅a+b2−2aba 的值是
A. −1B. 1C. −3D. 3

7. 下面的统计图反映了我国出租车（巡游出租车和网约出租车）客运量结构变化．
（以上数据摘自《中国共享经济发展年度报告 2019 》）
根据统计图提供的信息，下列推断合理的是
A. 2018 年与 2017 年相比，我国网约出租车客运量增加了 20% 以上
B. 2018 年，我国巡游出租车客运量占出租车客运总量的比例不足 60%
C. 2015 年至 2018 年，我国出租车客运的总量一直未发生变化
D. 2015 年至 2018 年，我国巡游出租车客运量占出租车客运总量的比例逐年增加

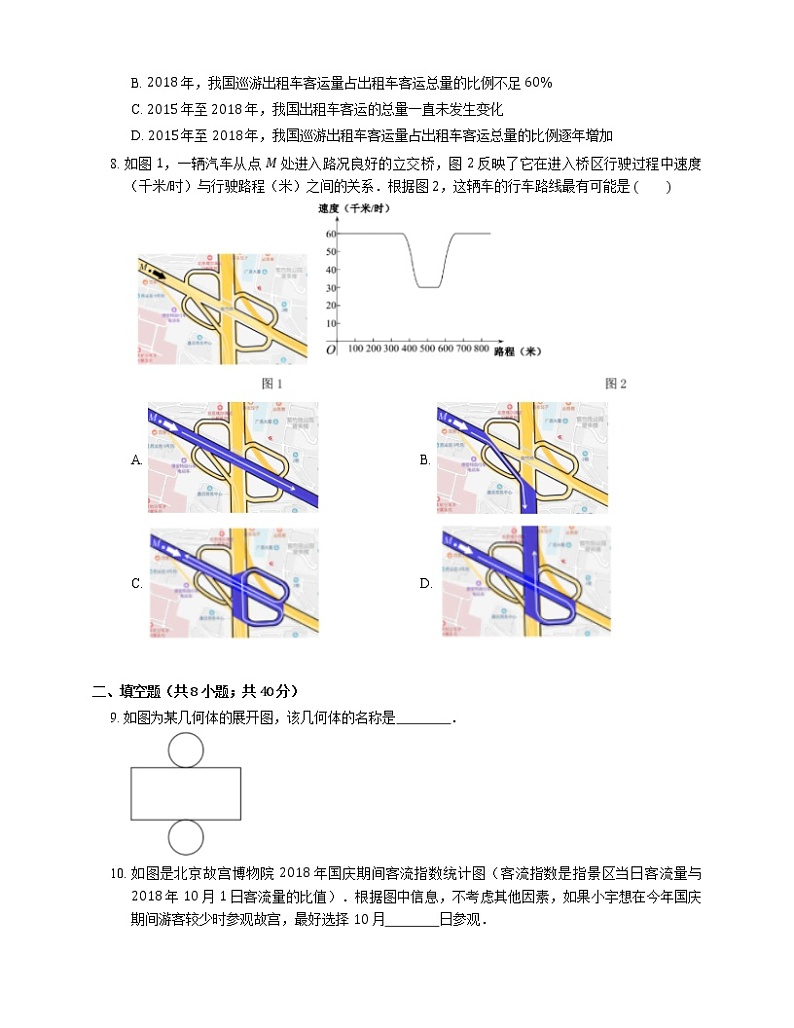
8. 如图 1，一辆汽车从点 M 处进入路况良好的立交桥，图 2 反映了它在进入桥区行驶过程中速度（千米/时）与行驶路程（米）之间的关系．根据图 2，这辆车的行车路线最有可能是
A. B.
C. D.

二、填空题（共8小题；共40分）
9. 如图为某几何体的展开图，该几何体的名称是 ．

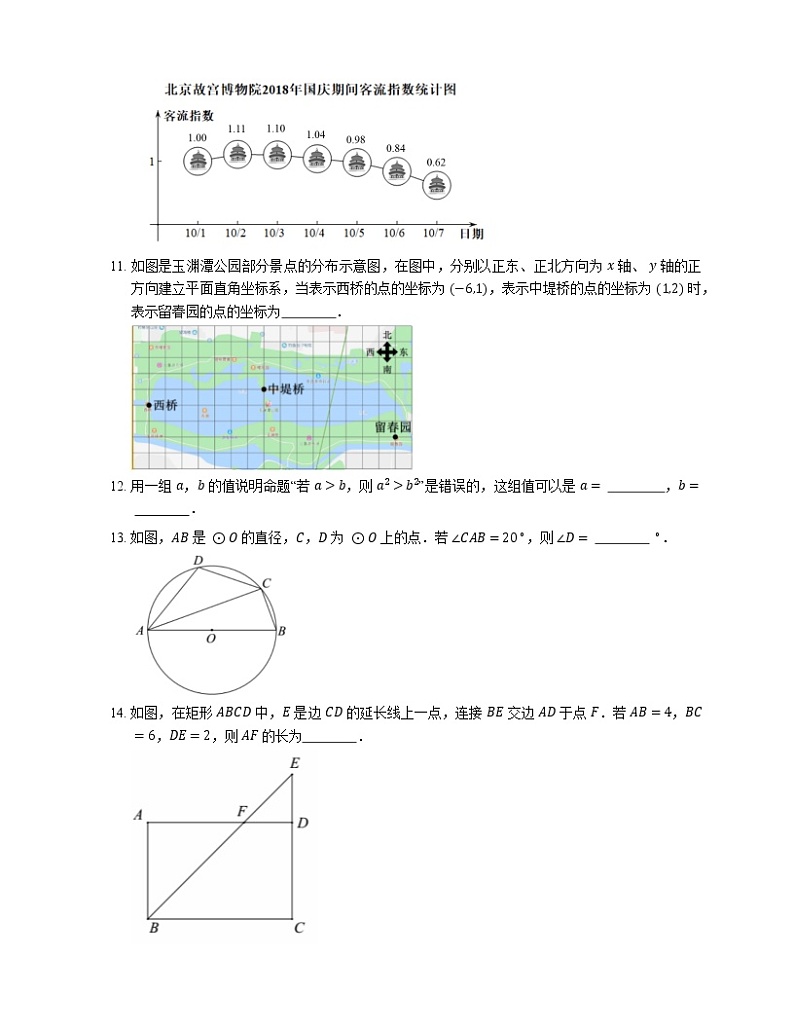
10. 如图是北京故宫博物院 2018 年国庆期间客流指数统计图（客流指数是指景区当日客流量与 2018 年 10 月 1 日客流量的比值）．根据图中信息，不考虑其他因素，如果小宇想在今年国庆期间游客较少时参观故宫，最好选择 10 月 日参观．

11. 如图是玉渊潭公园部分景点的分布示意图，在图中，分别以正东、正北方向为 x 轴、 y 轴的正方向建立平面直角坐标系，当表示西桥的点的坐标为 −6,1，表示中堤桥的点的坐标为 1,2 时，表示留春园的点的坐标为 ．

12. 用一组 a，b 的值说明命题“若 a>b，则 a2>b2”是错误的，这组值可以是 a= ，b= ．

13. 如图，AB 是 ⊙O 的直径，C，D 为 ⊙O 上的点．若 ∠CAB=20∘，则 ∠D= ∘．

14. 如图，在矩形 ABCD 中，E 是边 CD 的延长线上一点，连接 BE 交边 AD 于点 F．若 AB=4，BC=6，DE=2，则 AF 的长为 ．

15. 2019 年 2 月，全球首个 5G 火车站在上海虹桥火车站启动．虹桥火车站中 5G 网络峰值速率为 4G 网络峰值速率的 10 倍．在峰值速率下传输 8 千兆数据，5G 网络比 4G 网络快 720 秒，求这两种网络的峰值速率．设 4G 网络的峰值速率为每秒传输 x 千兆数据，依题意，可列方程为 ．

16. 小宇计划在某外卖网站点如表所示的菜品．已知每份订单的配送费为 3 元，商家为了促销，对每份订单的总价（不含配送费）提供满减优惠：满 30 元减 12 元，满 60 元减 30 元，满 100 元减 45 元．如果小宇在购买下表中的所有菜品时，采取适当的下订单方式，那么他点餐的总费用最低可为 元．

三、解答题（共12小题；共156分）
17. 计算：4sin60∘+π−10−12+∣3−1∣．

18. 解不等式组：5x−1>2x+1,3x+24>x.

19. 下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程．
已知：直线 l 及直线 l 外一点 P．
求作：直线 PQ，使 PQ∥l．
作法：如图，
①在直线 l 上取一点 O，以点 O 为圆心，OP 长为半径画半圆，交直线 l 于 A，B 两点；
②连接 PA，以 B 为圆心，AP 长为半径画弧，交半圆于点 Q；
③作直线 PQ．
所以直线 PQ 就是所求作的直线．
根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：连接 PB，QB，
∵PA=QB，
∴PA= ，
∴∠PBA=∠QPB（ ）（填推理的依据），
∴PQ∥l（ ）（填推理的依据）．

20. 关于 x 的一元二次方程 ax2+2ax+c=0．
（1）若方程有两个相等的实数根，请比较 a，c 的大小，并说明理由．
（2）若方程有一个根是 0，求此时方程的另一个根．

21. 如图，在四边形 ABCD 中，AB∥CD，AB=BC=2CD，E 为对角线 AC 的中点，F 为边 BC 的中点，连接 DE，EF．
（1）求证：四边形 CDEF 为菱形；
（2）连接 DF 交 EC 于 G，若 DF=2，CD=53，求 AD 的长．

22. 如图，AB 是 ⊙O 的直径，弦 CD⊥AB 于点 E，在 ⊙O 的切线 CM 上取一点 P，使得 ∠CPB=∠COA．
（1）求证：PB 是 ⊙O 的切线；
（2）若 AB=43，CD=6，求 PB 的长．

23. 在平面直角坐标系 xOy 中，直线 y=2x+b 经过点 A1,m，B−1,−1．
（1）求 b 和 m 的值．
（2）将点 B 向右平移到 y 轴上，得到点 C，设点 B 关于原点的对称点为 D，记线段 BC 与 AD 组成的图形为 G．
①直接写出点 C，D 的坐标；
②若双曲线 y=kx 与图形 G 恰有一个公共点，结合函数图象，求 k 的取值范围．

24. 如图，线段 AB 及一定点 C，P 是线段 AB 上一动点，作直线 CP，过点 A 作 AQ⊥CP 于点 Q．已知 AB=7 cm，设 A，P 两点间的距离为 x cm，A，Q 两点间的距离为 y1 cm，P，Q 两点间的距离为 y2 cm．小明根据学习函数的经验，分别对函数 y1，y2 随自变量 x 的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整：
（1）按照下表中自变量 x 的值进行取点、画图、测量，分别得到了 y1，y2 与 x 的几组对应值：
（2）在同一平面直角坐标系 xOy 中，描出补全后的表中各组数值所对应的点 x,y1，x,y2，并画出函数 y1，y2 的图象；
（3）结合函数图象，解决问题：当 △APQ 中有一个角为 30∘ 时，AP 的长度约为 cm．

25. 为迎接 2022 年冬奥会，鼓励更多的学生参与到志愿服务中来，甲、乙两所学校组织了志愿服务团队选拔活动．经过初选，两所学校各 400 名学生进入综合素质展示环节．为了了解两所学校学生的整体情况，从两校进入综合素质展示环节的学生中分别随机抽取了 50 名学生的综合素质展示成绩（百分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息．
a. 甲学校学生成绩的频数分布直方图如图（数据分成 6 组：40≤x<50，50≤x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）．
b. 甲学校学生成绩在 80≤x<90 这一组的是：

c. 乙学校学生成绩的平均数、中位数、众数、优秀率（85 分及以上为优秀）如表．
根据以上信息，回答下列问题：
平均数中位数众数优秀率83.3847846%
（1）甲学校学生A，乙学校学生B的综合素质展示成绩同为 83 分，这两人在本校学生中的综合素质展示排名更靠前的是 （填“A”或“B”）．
（2）根据上述信息，推断 学校综合素质展示的水平更高，理由为 （至少从两个不同的角度说明推断的合理性）．
（3）若每所学校综合素质展示的前 120 名学生将被选入志愿服务团队，预估甲学校分数至少达到 分的学生才可以入选．

26. 在平面直角坐标系 xOy 中，抛物线 y=ax2+bx+ca>0 经过点 A0,−3 和 B3,0．
（1）求 c 的值及 a，b 满足的关系式；
（2）若抛物线在 A，B 两点间，从左到右上升，求 a 的取值范围；
（3）结合函数图象判断：抛物线能否同时经过点 M−1+m,n，N4−m,n?若能，写出一个符合要求的抛物线的表达式和 n 的值；若不能，请说明理由．

27. 如图，在等腰直角 △ABC 中，∠ABC=90∘，D 是线段 AC 上一点（CA>2CD），连接 BD，过点 C 作 BD 的垂线，交 BD 的延长线于点 E，交 BA 的延长线于点 F．
（1）依题意补全图形；
（2）若 ∠ACE=α，求 ∠ABD 的大小（用含 α 的式子表示）；
（3）若点 G 在线段 CF 上，CG=BD，连接 DG．
①判断 DG 与 BC 的位置关系并证明；
②用等式表示 DG，CG，AB 之间的数量关系为 ．

28. 对于平面直角坐标系 xOy 中的直线 l 和图形 M，给出如下定义：P1，P2，⋯，Pn−1，Pn 是图形 M 上的 nn≥3 个不同的点，记这些点到直线 l 的距离分别为 d1，d2，⋯，dn−1，dn，若这 n 个点满足 d1+d2+⋯+dn−1=dn，则称这 n 个点为图形 M 关于直线 l 的一个基准点列，其中 dn 为该基准点列的基准距离．
（1）当直线 l 是 x 轴，图形 M 上有三点 A−1,1，B1,−1，C0,2 时，判断 A，B，C 是否为图形 M 关于直线 l 的一个基准点列?如果是，求出它的基准距离；如果不是，请说明理由；
（2）已知直线 l 是函数 y=−3x+3 的图象，图形 M 是圆心在 y 轴上，半径为 1 的 ⊙T，P1，P2，⋯，Pn−1，Pn 是 ⊙T 关于直线 l 的一个基准点列．
①若 T 为原点，求该基准点列的基准距离 dn 的最大值；
②若 n 的最大值等于 6，直接写出圆心 T 的纵坐标 t 的取值范围．
答案
第一部分
1. B
2. A
3. A
4. C
5. C
6. B
7. A
8. D
第二部分
9. 圆柱
10. 7
11. 9,−1
12. −1，−2（答案不唯一）
13. 110
14. 4
15. 8x−810x=720
16. 54
第三部分
17. 原式=4×32+1−23+3−1=3.
18. 原不等式组为
5x−1>2x+1, ⋯⋯①3x+24>x. ⋯⋯②
解不等式 ①，得
x>1.
解不等式 ②，得
x<2∴
原不等式组的解集为
119. （1） 补全的图形如图所示：
（2） QB；等弧所对的圆周角相等；内错角相等，两直线平行
20. （1） 依题意可知，a≠0，Δ=0．
∴4aa−c=0．
∴a=c．
（2） ∵ 方程有一个根是 0，
∴c=0．
∴ax2+2ax=0，
即 axx+2=0．
∴ 方程的一个根为 x=−2．
21. （1） ∵E，F 分别为 AC，BC 的中点，
∴EF∥AB，EF=12AB，CF=12BC．
∵AB∥CD，
∴EF∥CD．
∵AB=2CD，
∴EF=CD．
∴ 四边形 CDEF 是平行四边形．
∵AB=BC，
∴CF=EF．
∴ 四边形 CDEF 是菱形．
（2） ∵ 四边形 CDEF 是菱形，DF=2，
∴DF⊥AC，DG=12DF=1．
在 Rt△DGC 中，CD=53，可得 CG=CD2−DG2=43．
∴EG=CG=43，CE=2CG=83．
∵E 为 AC 中点，
∴AE=CE=83．
∴AG=AE+EG=4．
在 Rt△DGA 中，AD=AG2+DG2=17．
22. （1） ∵PC 与 ⊙O 相切于点 C，
∴OC⊥PC．
∴∠OCP=90∘．
∵∠AOC=∠CPB，∠AOC+∠BOC=180∘，
∴∠BOC+∠CPB=180∘．
在四边形 PBOC 中，∠PBO=360∘−∠CPB−∠BOC−∠PCO=90∘．
∴ 半径 OB⊥PB．
∴PB 是 ⊙O 的切线．
（2） 解法 1：
连接 OP，如图．
∵AB 是 ⊙O 的直径，AB=43，
∴OC=OB=12AB=23．
∵ 弦 CD⊥AB 于点 E，CD=6，
∴CE=12CD=3．
在 Rt△CEO 中，sin∠COE=CECO=32．
∴∠COE=60∘．
∵PB，PC 都是 ⊙O 的切线，
∴∠CPO=∠BPO，∠OCP=∠OBP．
∴∠COP=∠BOP=60∘．
∴PB=OB⋅tan60∘=6．
【解析】解法 2：
连接 BC，如图．
∵AB 是 ⊙O 的直径，AB=43，
∴OC=12AB=23，
∵ 弦 CD⊥AB 于点 E，CD=6，
∴CE=12CD=3．
在 Rt△CEO 中，sin∠COE=CECO=32，
∴∠COE=60∘，
∴∠CPB=∠COE=60∘，∠ABC=12∠COE=30∘．
∴BC=2CE=6．
∵PB，PC 都是 ⊙O 的切线，
∴PB=PC．
∴△PBC 为等边三角形．
∴PB=BC=6．
23. （1） ∵ 直线 y=2x+b 经过点 A1,m，B−1,−1，
∴b=1．
又 ∵ 直线 y=2x+b 经过点 A1,m，
∴m=3．
（2） ① C0,−1，D1,1．
②函数 y=kx 的图象经过点 A 时，k=3．
函数 y=kx 的图象经过点 D 时，k=1，此时双曲线也经过点 B，
结合图象可得 k 值得范围是 024. （1） ∵ 过点 A 作 AQ⊥CP 于点 Q，设 A，P 两点间的距离为 x cm，A，Q 两点间的距离为 y1 cm，P，Q 两点间的距离为 y2 cm，
∴x2=y12+y22，
∴ 当 x=4，y1=2.61，
∴y2=42−2.612=3.02．
（2） 利用描点法画出函数图象如图所示：．
（3） 当 △APQ 中有一个角为 30∘ 时，x=2y1，y2=3y1，
∴x=5.49或2.50．
25. （1） A
（2） 乙；甲校优秀率 40%，低于乙校，说明乙校综合展示水平优秀人数更多
【解析】通过图表，估计甲校平均数为 79 ，低于乙校，说明乙校整体水平高于甲校；
甲校中位数为 81.25，乙校为 84，说明乙校综合展示水平一半的同学高于 84 分，而甲校一半同学的综合展示水平仅高于 81.25．
综合以上三个（两个）理由，说明乙校的综合素质展示水平更高．
（3） 88.5
26. （1） 由题意可得 −3=c,0=9a+3b+c,
∴c=−3，3a+b−1=0．
（2） 由（1）可得 y=ax2+1−3ax−3a>0．
∵ 抛物线在 A，B 两点间，从左到右上升，
∴3a−12a≤0．
∵a>0，
∴3a−1≤0，即 0 （3） 抛物线不能经过点 M−1+m,n，N4−m,n．
理由如下：
若抛物线经过 M−1+m,n，N4−m,n，则抛物线的对称轴为 x=32．
由抛物线经过点 A，可知抛物线经过点 3,−3，与抛物线经过点 B3,0 矛盾．
所以抛物线不能经过点 M−1+m,n，N4−m,n．
27. （1） 补全图形，如图．
（2） ∵AB=BC，∠ABC=90∘，
∴∠BAC=∠BCA=45∘．
∵∠ACE=α，
∴∠ECB=45∘+α．
∵CF⊥BD 交 BD 的延长线于点 E，
∴∠BEF=90∘．
∴∠F+∠ABD=90∘．
∵∠F+∠ECB=90∘，
∴∠ABD=∠ECB=45∘+α．
（3） ① DG 与 BC 的位置关系：DG⊥BC．
证明：连接 BG 交 AC 于点 M，延长 GD 交 BC 于点 H，如图．
∵AB=BC，∠ABD=∠ECB，BD=CG，
∴△ABD≌△BCG．
∴∠CBG=∠BAD=45∘．
∴∠ABG=∠CBG=∠BAC=45∘．
∴AM=BM，∠AMB=90∘．
∵AD=BG，
∴DM=GM．
∴∠MGD=∠GDM=45∘．
∴∠BHG=90∘，
∴DG⊥BC．
② 2CG2=DG2+AB2．
28. （1） 是．
∵A−1,1，B0,2，C1,−1 到 x 轴的距离分别是 1，1，2，且 1+1=2，
∴ 这三点为图形 M 关于直线 l 的一个基准点列，它的基准距离为 2．
（2） ① ∵P1，P2，⋯，Pn−1，Pn 是 ⊙T 关于直线 l 的一个基准点列，
∴d1+d2+⋯+dn−1=dn．
∴dn 的最大值为 ⊙T 上的点到直线 l 的最大距离．
当 T 为原点时，过 O 作 OH⊥l 于点 H，延长 HO 交 ⊙O 于点 F，
则 FH 的长度为 dn 的最大值．
设函数 y=−3x+3 的图象与 x 轴，y 轴分别交于点 D，E，
则 D3,0，E0,3．
∴OD=3，OE=3，∠DOE=90∘．
∴∠OED=30∘．
又 ∵∠OHE=90∘，
∴OH=12OE=32．
∴FH=52．
例如，⊙O 上存在点 P1，P2，P3，P4 满足 d1=12，d2=34，d3=54，d4=52．
∴dn 的最大值为 52．
②圆心 T 的纵坐标 t 的取值范围为 0