2017-2021年陕西中考数学真题分类汇编之图形的性质

这是一份2017-2021年陕西中考数学真题分类汇编之图形的性质，共49页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2017-2021年陕西中考数学真题分类汇编之图形的性质
一、选择题（共10小题）
1．（2021•陕西）如图，、、、是四根长度均为的火柴棒，点、、共线．若，，则线段的长度是　　

A． B． C． D．
2．（2021•陕西）如图，点、分别在线段、上，连接、．若，，，则的大小为　　

A． B． C． D．
3．（2020•陕西）若，则余角的大小是　　
A． B． C． D．
4．（2020•陕西）如图，，直线经过点，若，则的大小为　　

A． B． C． D．
5．（2019•陕西）如图，在中，，，平分交于点，，垂足为．若，则的长为　　

A． B． C． D．3
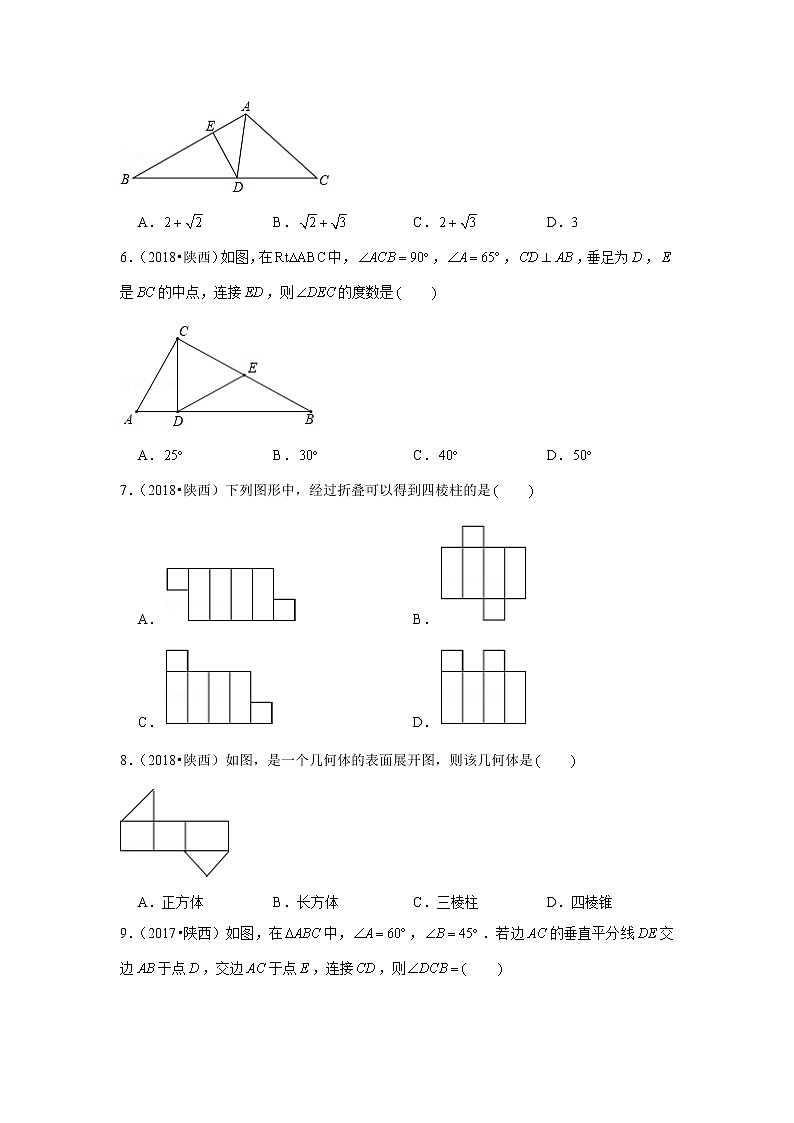
6．（2018•陕西）如图，在中，，，，垂足为，是的中点，连接，则的度数是　　

A． B． C． D．
7．（2018•陕西）下列图形中，经过折叠可以得到四棱柱的是　　
A． B．
C． D．
8．（2018•陕西）如图，是一个几何体的表面展开图，则该几何体是　　

A．正方体 B．长方体 C．三棱柱 D．四棱锥
9．（2017•陕西）如图，在中，，．若边的垂直平分线交边于点，交边于点，连接，则　　

A． B． C． D．
10．（2017•陕西）如图，直线，的直角顶点落在直线上，若，则的大小为　　

A． B． C． D．
二、填空题（共10小题）
11．（2021•陕西）如图，正方形的边长为4，的半径为1．若在正方形内平移可以与该正方形的边相切），则点到上的点的距离的最大值为 　　．

12．（2021•陕西）正九边形一个内角的度数为 　　．
13．（2020•陕西）如图，在菱形中，，，点在边上，且．若直线经过点，将该菱形的面积平分，并与菱形的另一边交于点，则线段的长为　　．

14．（2020•陕西）如图，在正五边形中，是边的延长线，连接，则的度数是　　．

15．（2020•陕西）如图，在矩形中，，，延长至，使，以为边向右侧作正方形，为正方形的中心，若过点的一条直线平分该组合图形的面积，并分别交、于点、，则线段的长为　　．

16．（2020•陕西）如图，为正五边形的边上一点，过点作，交于点，则的度数为　　．

17．（2018•陕西）如图，在矩形中，，，连接，是的中点，是上一点，且，是上一动点，则的最大值为　　．

18．（2018•陕西）如图，在正五边形中，与相交于点，则的度数为　　．

19．（2017•陕西）如图，在四边形中，，，连接．若，则四边形的面积为　　．

20．（2017•陕西）如图．在中，，，是的角平分线，过点作交边于点．若，则图中阴影部分的面积为　　

三、解答题（共10小题）
21．（2020•陕西）如图，已知，是边延长线上一定点，请用尺规作图法，在边的延长线上求作一点，使．（保留作图痕迹，不写作法）

22．（2020•陕西）如图，在四边形中，，．是边上一点，且．求证：．

23．（2019•陕西）问题提出：
（1）如图1，已知，试确定一点，使得以，，，为顶点的四边形为平行四边形，请画出这个平行四边形；
问题探究：
（2）如图2，在矩形中，，，若要在该矩形中作出一个面积最大的，且使，求满足条件的点到点的距离；
问题解决：
（3）如图3，有一座塔，按规定，要以塔为对称中心，建一个面积尽可能大的形状为平行四边形的景区．根据实际情况，要求顶点是定点，点到塔的距离为50米，，那么，是否可以建一个满足要求的面积最大的平行四边形景区？若可以，求出满足要求的平行四边形的最大面积；若不可以，请说明理由．（塔的占地面积忽略不计）

24．（2019•陕西）如图，的半径，过点作的切线，且，连接并延长，与交于点、，过点作，并与交于点，连接、．
（1）求证：；
（2）求的长．

25．（2019•陕西）如图，在中，，是边上的高．请用尺规作图法，求作的外接圆．（保留作图痕迹，不写作法）

26．（2018•陕西）问题提出
（1）如图①，在中，，，点关于所在直线的对称点为，则的长度为　　．
问题探究
（2）如图②，半圆的直径，是的中点，点在上，且，是上的动点，试求的最小值．
问题解决
（3）如图③，扇形花坛的半径为，．根据工程需要．现想在上选点，在边上选点，在边上选点，用装饰灯带在花坛内的地面上围成一个，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带的长度最短，并且用长度最短的灯带围成的为等腰三角形．试求的值最小时的等腰的面积．（安装损耗忽略不计）

27．（2018•陕西）如图，，、分别为、上的点，且，连接，分别与、相交于点，，若，求证：．

28．（2018•陕西）如图，在中，，是的外接圆，点在上，且，过点作的垂线，与的延长线相交于点，并与的延长线相交于点．
（1）求证：是的切线；
（2）若的半径，，求的长．

29．（2017•陕西）如图，在正方形中，、分别为边和上的点，且，连接、交于点．求证：．

30．（2017•陕西）如图，在中，延长到点，延长到点，使，连接交边于点，交边于点．求证：．


2017-2021年陕西中考数学真题分类汇编之图形的性质
参考答案与试题解析
一、选择题（共10小题）
1．（2021•陕西）如图，、、、是四根长度均为的火柴棒，点、、共线．若，，则线段的长度是　　

A． B． C． D．
【答案】
【考点】全等三角形的应用；勾股定理的应用
【专题】几何直观；推理能力；运算能力；等腰三角形与直角三角形；图形的全等
【分析】过作于，过作于，由等腰三角形的性质得到，，根据全等三角形判定证得，得到，在中，根据勾股定理求出，进而求出．
【解答】解：由题意知，，，
过作于，过作于，
则，，，
，
，
，
，
在和中，
，
，
，
在中，
，，
，
，
，
故选：．

【点评】本题主要考查了等腰三角形的性质和判定，等腰三角形的性质，勾股定理，正确作出辅助线，证得是解决问题的关键．
2．（2021•陕西）如图，点、分别在线段、上，连接、．若，，，则的大小为　　

A． B． C． D．
【答案】
【考点】三角形内角和定理；三角形的外角性质
【专题】三角形；运算能力
【分析】由三角形的内角和定理，可得，，所以，由此解答即可．
【解答】解：，，
，
，
，
，
故选：．
【点评】本题考查了三角形内角和定理和三角形外角性质，掌握这些知识点是解题的关键．
3．（2020•陕西）若，则余角的大小是　　
A． B． C． D．
【考点】：余角和补角
【专题】66：运算能力；551：线段、角、相交线与平行线
【分析】根据的余角是，代入求出即可．
【解答】解：，
的余角是．
故选：．
【点评】本题考查了互余的应用，注意：如果和互为余角，那么．
4．（2020•陕西）如图，，直线经过点，若，则的大小为　　

A． B． C． D．
【答案】
【考点】垂线
【专题】线段、角、相交线与平行线；推理能力
【分析】由垂线的性质可得，由平角的性质可求解．
【解答】解：，
，
，
，
故选：．
【点评】本题考查了垂线的性质，平角的性质，是基础题．
5．（2019•陕西）如图，在中，，，平分交于点，，垂足为．若，则的长为　　

A． B． C． D．3
【考点】：角平分线的性质
【专题】551：线段、角、相交线与平行线
【分析】过点作于如图所示，根据角平分线的性质得到，解直角三角形即可得到结论．
【解答】解：过点作于，如图所示，
为的平分线，且于，于，
，
在中，，
，
在中，，
为等腰直角三角形，
，
，
故选：．

【点评】本题考查了角平分线的性质，解直角三角形，正确的作出辅助线是解题的关键．
6．（2018•陕西）如图，在中，，，，垂足为，是的中点，连接，则的度数是　　

A． B． C． D．
【考点】：直角三角形斜边上的中线
【专题】554：等腰三角形与直角三角形；69：应用意识
【分析】利用三角形内角和定理和直角三角形斜边中线的性质解决问题即可．
【解答】解：，，
，
，
，
，
，
，
，
，
故选：．
【点评】本题考查直角三角形斜边中线的性质，三角形内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
7．（2018•陕西）下列图形中，经过折叠可以得到四棱柱的是　　
A． B．
C． D．
【考点】：展开图折叠成几何体
【专题】63：空间观念；55：几何图形
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．
【解答】解：、经过折叠，不能围成封闭的长方体；
、两个正方形围起来构成长方体的上下底面，四个长方形围成长方体的侧面，故可以围成一个四棱柱；
、经过折叠，不能围成封闭的长方体；
、经过折叠，不能围成封闭的长方体；
故选：．
【点评】本题主要考查了展开图折成几何体，棱柱表面展开图中，上、下两底面应在侧面展开图长方形的两侧．
8．（2018•陕西）如图，是一个几何体的表面展开图，则该几何体是　　

A．正方体 B．长方体 C．三棱柱 D．四棱锥
【考点】：几何体的展开图
【专题】28：操作型
【分析】由展开图得这个几何体为棱柱，底面为三边形，则为三棱柱．
【解答】解：由图得，这个几何体为三棱柱．
故选：．
【点评】考查了几何体的展开图，有两个底面的为柱体，有一个底面的为锥体．
9．（2017•陕西）如图，在中，，．若边的垂直平分线交边于点，交边于点，连接，则　　

A． B． C． D．
【考点】：线段垂直平分线的性质
【专题】552：三角形；67：推理能力
【分析】依据三角形内角和定理即可得到的度数，再根据垂直平分线的性质，即可得出的度数，进而得到的度数．
【解答】解：，，
，
垂直平分，
，
，
，
故选：．
【点评】本题主要考查了线段垂直平分线的性质，线段垂直平分线上任意一点，到线段两端点的距离相等．
10．（2017•陕西）如图，直线，的直角顶点落在直线上，若，则的大小为　　

A． B． C． D．
【考点】：平行线的性质
【专题】551：线段、角、相交线与平行线
【分析】由余角的定义求出的度数，再根据平行线的性质求出的度数，即可得出结论．
【解答】解：，，
．
，
．
故选：．

【点评】本题考查的是平行线的性质，解题时注意：两直线平行，同位角相等．
二、填空题（共10小题）
11．（2021•陕西）如图，正方形的边长为4，的半径为1．若在正方形内平移可以与该正方形的边相切），则点到上的点的距离的最大值为 　　．

【考点】直线与圆的位置关系；切线的性质；平移的性质；正方形的性质
【专题】与圆有关的位置关系；推理能力
【分析】当与、相切时，点到上的点的距离最大，如图，过点作于，于，根据切线的性质得到，利用正方形的性质得到点在上，然后计算出的长即可．
【解答】解：当与、相切时，点到上的点的距离最大，如图，
过点作于，于，
，
平分，
四边形为正方形，
点在上，
，，
，
即点到上的点的距离的最大值为，
故答案为．

【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了正方形的性质．
12．（2021•陕西）正九边形一个内角的度数为 　　．
【考点】多边形内角与外角
【专题】多边形与平行四边形；推理能力
【分析】先根据多边形内角和定理：求出该多边形的内角和，再求出每一个内角的度数．
【解答】解：该正九边形内角和，
则每个内角的度数．
故答案为：．
【点评】本题主要考查了多边形的内角和定理：，比较简单，解答本题的关键是直接根据内角和公式计算可得内角和．
13．（2020•陕西）如图，在菱形中，，，点在边上，且．若直线经过点，将该菱形的面积平分，并与菱形的另一边交于点，则线段的长为　　．

【考点】：菱形的性质
【专题】67：推理能力；17：推理填空题；556：矩形 菱形 正方形；66：运算能力
【分析】过点和点作，于点和，可得矩形，再根据菱形中，，，可得，，由题意可得，，进而根据勾股定理可得的长．
【解答】解：如图，过点和点作，于点和，
得矩形，
，

在菱形中，，，
，，
，
平分菱形面积，经过菱形对角线交点，
，
，
在中，根据勾股定理，得
．
故答案为：．
【点评】本题考查了菱形的性质，解决本题的关键是掌握菱形的性质．
14．（2020•陕西）如图，在正五边形中，是边的延长线，连接，则的度数是　　．

【考点】多边形内角与外角
【专题】正多边形与圆；多边形与平行四边形；运算能力
【分析】根据正五边形的性质和内角和为，求得每个内角的度数为，再结合等腰三角形和邻补角的定义即可解答．
【解答】解：因为五边形是正五边形，
所以，，
所以，
所以，
故答案为：．
【点评】本题考查了正五边形．解题的关键是掌握正五边形的性质：各边相等，各角相等，内角和为．熟记定义是解题的关键．
15．（2020•陕西）如图，在矩形中，，，延长至，使，以为边向右侧作正方形，为正方形的中心，若过点的一条直线平分该组合图形的面积，并分别交、于点、，则线段的长为　　．

【答案】．
【考点】矩形的性质；正方形的性质
【专题】矩形 菱形 正方形；推理能力
【分析】连接，交于点，过点和点的直线平分该组合图形的面积，交于，取中点，取中点，连接，，过点作于，由三角形中位线定理可求，，，，，，由平行线分线段成比例可得，由勾股定理可求的长，即可求解．
【解答】解：如图，连接，交于点，过点和点的直线平分该组合图形的面积，交于，取中点，取中点，连接，，过点作于，

四边形是矩形，
，
又是中点，
，，，
同理可求，，，
，，
，，
，
四边形是矩形，
，，
，
，
，
故答案为：．
【点评】本题考查了正方形的性质，矩形的性质，三角形中位线定理，平行线分线段成比例，灵活运用这些性质解决问题是本题的关键．
16．（2020•陕西）如图，为正五边形的边上一点，过点作，交于点，则的度数为　　．

【答案】．
【考点】平行线的性质；多边形内角与外角
【专题】正多边形与圆；推理能力
【分析】连接，由正五边形的性质可得，，由等腰三角形的性质可求，可证，由平行线的性质可求解．
【解答】解：连接，

五边形是正五边形，
，，
，
，
，
，
，
，
，
故答案为：．
【点评】本题考查了多边形的内角和外角，等腰三角形的性质，平行线的性质，灵活运用这些性质解决问题是本题的关键．
17．（2018•陕西）如图，在矩形中，，，连接，是的中点，是上一点，且，是上一动点，则的最大值为　　．

【考点】：三角形三边关系；：矩形的性质
【专题】67：推理能力；558：平移、旋转与对称
【分析】连接并延长交于，则此时，的值最大，且的最大值，根据全等三角形的性质得到，，求得，过作于，得到四边形是矩形，得到，，根据勾股定理即可得到结论．
【解答】解：在矩形中，，，
，
连接并延长交于，
则此时，的值最大，且的最大值，
，
，
，，
，
，，
，
过作于，
四边形是矩形，
，，
，
，
，
故答案为：．

【点评】本题考查了轴对称最短路线问题，矩形的性质，勾股定理，全等三角形的判定和性质，正确的作出辅助线是解题的关键．
18．（2018•陕西）如图，在正五边形中，与相交于点，则的度数为　　．

【考点】：多边形内角与外角；：正多边形和圆
【专题】552：三角形
【分析】根据五边形的内角和公式求出，根据等腰三角形的性质，三角形外角的性质计算即可．
【解答】解：五边形是正五边形，
，
，
，
同理，
，
故答案为：．
【点评】本题考查的是正多边形的内角与外角，掌握正多边形的内角的计算公式、等腰三角形的性质是解题的关键
19．（2017•陕西）如图，在四边形中，，，连接．若，则四边形的面积为　18　．

【考点】全等三角形的判定与性质
【分析】作辅助线；证明，得到，与的面积相等；求出正方形的面积即可解决问题．
【解答】解：如图，作、，交的延长线于点；

四边形为矩形，；
，
；
在与中，
，
，
（设为；与的面积相等；
四边形的面积正方形的面积；
由勾股定理得：，而；
，，
故答案为：18．

【点评】本题主要考查了全等三角形的判定及其性质、正方形的判定及其性质等几何知识点的应用问题；解题的关键是作辅助线，构造全等三角形和正方形．
20．（2017•陕西）如图．在中，，，是的角平分线，过点作交边于点．若，则图中阴影部分的面积为　1　

【考点】三角形的面积；勾股定理
【专题】三角形
【分析】作于，由题意可得，是等腰直角三角形，设，证明，可得，，在中，由勾股定理可得，即，，根据阴影部分的面积三角形的面积三角形的面积，即可得出图中阴影部分的面积．
【解答】解：如图，作于，
，是的角平分线，
，
，
，
是等腰直角三角形，
设，

，
，
，，
，
，，
，
，，
图中阴影部分的面积．
解法二：将绕点顺时针旋转得到．

，，
，
，，共线，
图中阴影部分的面积．
故答案为：1．

【点评】本题考查三角形面积的计算，相似三角形的判定和性质，勾股定理，解题的关键是用来表示出直角边，的长．
三、解答题（共10小题）
21．（2020•陕西）如图，已知，是边延长线上一定点，请用尺规作图法，在边的延长线上求作一点，使．（保留作图痕迹，不写作法）

【考点】作图基本作图
【专题】应用意识；作图题
【分析】作，射线交于点，点即为所求．
【解答】解：如图，点即为所求．

【点评】本题考查作图基本作图，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
22．（2020•陕西）如图，在四边形中，，．是边上一点，且．求证：．

【考点】平行四边形的判定与性质
【专题】推理能力；多边形与平行四边形
【分析】根据等边对等角的性质求出，再由得，所以，得出四边形是平行四边形，进而得出结论．
【解答】证明：，
．
，
，
，
，
四边形是平行四边形．
．
【点评】本题主要考查了平行四边形的判定和性质．解题的关键是熟练掌握平行四边形的判定定理和性质定理的运用．
23．（2019•陕西）问题提出：
（1）如图1，已知，试确定一点，使得以，，，为顶点的四边形为平行四边形，请画出这个平行四边形；
问题探究：
（2）如图2，在矩形中，，，若要在该矩形中作出一个面积最大的，且使，求满足条件的点到点的距离；
问题解决：
（3）如图3，有一座塔，按规定，要以塔为对称中心，建一个面积尽可能大的形状为平行四边形的景区．根据实际情况，要求顶点是定点，点到塔的距离为50米，，那么，是否可以建一个满足要求的面积最大的平行四边形景区？若可以，求出满足要求的平行四边形的最大面积；若不可以，请说明理由．（塔的占地面积忽略不计）

【考点】四边形综合题
【专题】几何综合题
【分析】（1）利用平行四边形的判定方法画出图形即可．
（2）以点为圆心，长为半径作，一定于相交于，两点，点，即为所求．
（3）可以，如图所示，连接，作的外接圆，则点在优弧上，取的中点，连接，，四边形即为所求．
【解答】解：（1）如图记为点所在的位置．

（2）如图，

，，取的中点，则．
以点为圆心，长为半径作，一定于相交于，两点，
连接，，，，点不能在矩形外；
的顶点或位置时，的面积最大，
作，垂足为，则，
，
由对称性得．

（3）可以，如图所示，连接，

为的对称中心，，，
，
作的外接圆，则点在优弧上，取的中点，连接，，
则，且，△为正三角形．
连接并延长，经过点至，使，连接，，
，
四边形为菱形，且，
作，垂足为，连接，则，
，

所以符合要求的的最大面积为．
【点评】本题属于四边形综合题，考查了平行四边形的判定和性质，圆周角定理，三角形的面积等知识，解题的关键是理解题意，学会添加常用辅助线，属于中考压轴题．
24．（2019•陕西）如图，的半径，过点作的切线，且，连接并延长，与交于点、，过点作，并与交于点，连接、．
（1）求证：；
（2）求的长．

【考点】：切线的性质
【专题】67：推理能力；：与圆有关的位置关系
【分析】（1）根据切线的性质得到，根据圆周角定理得到，根据平行线的性质和判定定理即可得到结论；
（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．
【解答】（1）证明：是的切线，
，
是的直径，
，
，
，
，
；
（2）解：，，
延长交于点，
则，，，
在中，，
由（1）知，，
，
即，
，，
，，
在中，．

【点评】本题考查了切线的性质，圆周角定理，平行线的判定和性质，勾股定理，相似三角形的判定和性质，正确的识别图形是解题的关键．
25．（2019•陕西）如图，在中，，是边上的高．请用尺规作图法，求作的外接圆．（保留作图痕迹，不写作法）

【考点】：等腰三角形的性质；：三角形的外接圆与外心；：作图复杂作图
【专题】13：作图题
【分析】作线段的垂直平分线，交于点，以为圆心，为半径作，即为所求．
【解答】解：如图所示：即为所求．

【点评】本题考查作图复杂作图，等腰三角形的性质，三角形的外接圆与外心等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
26．（2018•陕西）问题提出
（1）如图①，在中，，，点关于所在直线的对称点为，则的长度为　　．
问题探究
（2）如图②，半圆的直径，是的中点，点在上，且，是上的动点，试求的最小值．
问题解决
（3）如图③，扇形花坛的半径为，．根据工程需要．现想在上选点，在边上选点，在边上选点，用装饰灯带在花坛内的地面上围成一个，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带的长度最短，并且用长度最短的灯带围成的为等腰三角形．试求的值最小时的等腰的面积．（安装损耗忽略不计）

【考点】：圆的综合题
【专题】152：几何综合题；69：应用意识
【分析】（1）证明是等腰直角三角形，利用勾股定理求解即可．
（2）如图②中，作点关于的对称点，连接交于，连接，此时的值最小，过点作于．利用勾股定理求出即可解决问题．
（3）如图③中，连接，作点关于的对称点，点关于的对称点，连接交于，交于，连接，，，，此时的周长最小，再证明，利用等腰直角三角形的性质解决问题即可．
【解答】解：（1）如图①中，

，关于直线对称，
，，
，
，
故答案为．

（2）如图②中，作点关于的对称点，连接交于，连接，此时的值最小，过点作于．

是直径，，
，
，
，
，
，
是等边三角形，
，
，
，，
，，
，
，
的最小值．

（3）如图③中，连接，作点关于的对称点，点关于的对称点，连接交于，交于，连接，，，，此时的周长最小，

，，，
，
，
，
，
，，
，
，
，
，
，，
，，
，，
，
，
是等腰三角形，
，设，
则有，
解得，
．
【点评】本题属于圆综合题，考查了轴对称最短问题，等腰直角三角形的判定和性质，解直角三角形等知识，解题的关键是学会利用轴对称解决最短问题，属于中考压轴题．
27．（2018•陕西）如图，，、分别为、上的点，且，连接，分别与、相交于点，，若，求证：．

【考点】：平行线的性质；：全等三角形的判定与性质
【专题】14：证明题；553：图形的全等
【分析】由、知四边形是平行四边形、，从而得出、，结合知，根据可得，据此即可得证．
【解答】证明：、，
四边形是平行四边形，，
，，
，
，
，
在和中，
，
，
．
【点评】本题主要考查全等三角形的判定与性质，解题的关键是掌握平行线的性质与平行四边形的判定与性质及全等三角形的判定与性质．
28．（2018•陕西）如图，在中，，是的外接圆，点在上，且，过点作的垂线，与的延长线相交于点，并与的延长线相交于点．
（1）求证：是的切线；
（2）若的半径，，求的长．

【考点】切线的判定与性质
【专题】几何综合题；与圆有关的计算
【分析】（1）证明圆的切线主要从2个思路：作半径，证垂直；作垂直，证半径；
（2）求边的长，可以通过证三角形相似，边成比例来求其中一条边的长度；由（1）可以知道四边形是矩形，根据矩形的性质可以证明，那么，再结合勾股定理求的长，最后把已知的、、长度代入，即可以求出．
【解答】解：（1）如图，作于，
，，经过圆心点，
又，
，又

四边形是矩形，

是的切线
（2）由（1）知，四边形是矩形，
，


的半径，



．

【点评】该题目是圆与几何图形的综合题目，考查的知识有切线的证明、矩形的性质、勾股定理的应用、三角形相似比等，注意思路的构建．
29．（2017•陕西）如图，在正方形中，、分别为边和上的点，且，连接、交于点．求证：．

【考点】：正方形的性质；：全等三角形的判定与性质
【分析】根据正方形的性质，可得，，根据全等三角形的判定与性质，可得答案．
【解答】证明：四边形是正方形，
，．
，
，
在和中，
，
，
在和中，，
，
．
【点评】本题考查了正方形的性质，利用全等三角形的判定与性质是解题关键，又利用了正方形的性质．
30．（2017•陕西）如图，在中，延长到点，延长到点，使，连接交边于点，交边于点．求证：．

【考点】：全等三角形的判定与性质；：平行四边形的性质
【专题】555：多边形与平行四边形；553：图形的全等；64：几何直观
【分析】根据平行四边形的性质可得出，，利用即可证明，再根据全等三角形的性质即可求解．
【解答】证明：、分别是平行四边形的边、延长线上的点，
，
，
又平行四边形中，
，
又，
，
在与中，
，
，
，
．
【点评】本题考查了平行四边形的性质，解答本题的关键是掌握平行四边形的对边平行的性质及全等三角形的判定与性质．

考点卡片
1．几何体的展开图
（1）多数立体图形是由平面图形围成的．沿着棱剪开就得到平面图形，这样的平面图形就是相应立体图形的展开图．同一个立体图形按不同的方式展开，得到的平面展开图是不一样的，同时也可看出，立体图形的展开图是平面图形．
（2）常见几何体的侧面展开图：
①圆柱的侧面展开图是长方形．②圆锥的侧面展开图是扇形．③正方体的侧面展开图是长方形．④三棱柱的侧面展开图是长方形．
（3）立体图形的侧面展开图，体现了平面图形与立体图形的联系．立体图形问题可以转化为平面图形问题解决．
从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．
2．展开图折叠成几何体
通过结合立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形．
3．余角和补角
（1）余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．
（2）补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．
（3）性质：等角的补角相等．等角的余角相等．
（4）余角和补角计算的应用，常常与等式的性质、等量代换相关联．
注意：余角（补角）与这两个角的位置没有关系．不论这两个角在哪儿，只要度数之和满足了定义，则它们就具备相应的关系．
4．垂线
（1）垂线的定义
当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．
（2）垂线的性质
在平面内，过一点有且只有一条直线与已知直线垂直．
注意：“有且只有”中，“有”指“存在”，“只有”指“唯一”
“过一点”的点在直线上或直线外都可以．
5．平行线的性质
1、平行线性质定理
定理1：两条平行线被第三条直线所截，同位角相等． 简单说成：两直线平行，同位角相等．
定理2：两条平行线被地三条直线所截，同旁内角互补．．简单说成：两直线平行，同旁内角互补．
定理3：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
2、两条平行线之间的距离处处相等．
6．三角形的面积
（1）三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高．
（2）三角形的中线将三角形分成面积相等的两部分．
7．三角形三边关系
（1）三角形三边关系定理：三角形两边之和大于第三边．
（2）在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．
（3）三角形的两边差小于第三边．
（4）在涉及三角形的边长或周长的计算时，注意最后要用三边关系去检验，这是一个隐藏的定时炸弹，容易忽略．
8．三角形内角和定理
（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．
（2）三角形内角和定理：三角形内角和是180°．
（3）三角形内角和定理的证明
证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．
（4）三角形内角和定理的应用
主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．
9．三角形的外角性质
（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．
三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．
（2）三角形的外角性质：
①三角形的外角和为360°．
②三角形的一个外角等于和它不相邻的两个内角的和．
③三角形的一个外角大于和它不相邻的任何一个内角．
（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．
（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．
10．全等三角形的判定与性质
（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
11．全等三角形的应用
（1）全等三角形的性质与判定综合应用
用全等寻找下一个全等三角形的条件，全等的性质和判定往往是综合在一起应用的，这需要认真分析题目的已知和求证，分清问题中已知的线段和角与所证明的线段或角之间的联系．
（2）作辅助线构造全等三角形
常见的辅助线做法：①把三角形一边的中线延长，把分散条件集中到同一个三角形中是解决中线问题的基本规律．②证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，这些问题经常用到全等三角形来证明．
（3）全等三角形在实际问题中的应用
一般方法是把实际问题先转化为数学问题，再转化为三角形问题，其中，画出示意图，把已知条件转化为三角形中的边角关系是关键．
12．角平分线的性质
角平分线的性质：角的平分线上的点到角的两边的距离相等．
注意：①这里的距离是指点到角的两边垂线段的长；②该性质可以独立作为证明两条线段相等的依据，有时不必证明全等；③使用该结论的前提条件是图中有角平分线，有垂直角平分线的性质语言：如图，∵C在∠AOB的平分线上，CD⊥OA，CE⊥OB∴CD＝CE

13．线段垂直平分线的性质
（1）定义：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）垂直平分线，简称“中垂线”．
（2）性质：①垂直平分线垂直且平分其所在线段．　　　　②垂直平分线上任意一点，到线段两端点的距离相等．　　　　③三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等．
14．等腰三角形的性质
（1）等腰三角形的概念
有两条边相等的三角形叫做等腰三角形．
（2）等腰三角形的性质
①等腰三角形的两腰相等
②等腰三角形的两个底角相等．【简称：等边对等角】
③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．【三线合一】
（3）在①等腰；②底边上的高；③底边上的中线；④顶角平分线．以上四个元素中，从中任意取出两个元素当成条件，就可以得到另外两个元素为结论．
15．直角三角形斜边上的中线
（1）性质：在直角三角形中，斜边上的中线等于斜边的一半．（即直角三角形的外心位于斜边的中点）
（2）定理：一个三角形，如果一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形．
该定理可以用来判定直角三角形．
16．勾股定理
（1）勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．
（2）勾股定理应用的前提条件是在直角三角形中．
（3）勾股定理公式a2+b2＝c2 的变形有：a＝，b＝及c＝．
（4）由于a2+b2＝c2＞a2，所以c＞a，同理c＞b，即直角三角形的斜边大于该直角三角形中的每一条直角边．
17．勾股定理的应用
（1）在不规则的几何图形中，通常添加辅助线得到直角三角形．
（2）在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
（3）常见的类型：①勾股定理在几何中的应用：利用勾股定理求几何图形的面积和有关线段的长度．
②由勾股定理演变的结论：分别以一个直角三角形的三边为边长向外作正多边形，以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和．
③勾股定理在实际问题中的应用：运用勾股定理的数学模型解决现实世界的实际问题．
④勾股定理在数轴上表示无理数的应用：利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边．
18．多边形内角与外角
（1）多边形内角和定理：（n﹣2）•180° （n≥3且n为整数）
此公式推导的基本方法是从n边形的一个顶点出发引出（n﹣3）条对角线，将n边形分割为（n﹣2）个三角形，这（n﹣2）个三角形的所有内角之和正好是n边形的内角和．除此方法之和还有其他几种方法，但这些方法的基本思想是一样的．即将多边形转化为三角形，这也是研究多边形问题常用的方法．
（2）多边形的外角和等于360°．
①多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°．
②借助内角和和邻补角概念共同推出以下结论：外角和＝180°n﹣（n﹣2）•180°＝360°．
19．平行四边形的性质
（1）平行四边形的概念：有两组对边分别平行的四边形叫做平行四边形．
（2）平行四边形的性质：
①边：平行四边形的对边相等．
②角：平行四边形的对角相等．
③对角线：平行四边形的对角线互相平分．
（3）平行线间的距离处处相等．
（4）平行四边形的面积：
①平行四边形的面积等于它的底和这个底上的高的积．
②同底（等底）同高（等高）的平行四边形面积相等．
20．平行四边形的判定与性质
平行四边形的判定与性质的作用
平行四边形对应边相等，对应角相等，对角线互相平分及它的判定，是我们证明直线的平行、线段相等、角相等的重要方法，若要证明两直线平行和两线段相等、两角相等，可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上，通过证明四边形是平行四边形达到上述目的．
运用定义，也可以判定某个图形是平行四边形，这是常用的方法，不要忘记平行四边形的定义，有时用定义判定比用其他判定定理还简单．
凡是可以用平行四边形知识证明的问题，不要再回到用三角形全等证明，应直接运用平行四边形的性质和判定去解决问题．
21．菱形的性质
（1）菱形的定义：有一组邻边相等的平行四边形叫做菱形．
（2）菱形的性质
①菱形具有平行四边形的一切性质；
②菱形的四条边都相等；
③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；
④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．
（3）菱形的面积计算
①利用平行四边形的面积公式．
②菱形面积＝ab．（a、b是两条对角线的长度）
22．矩形的性质
（1）矩形的定义：有一个角是直角的平行四边形是矩形．
（2）矩形的性质
①平行四边形的性质矩形都具有；
②角：矩形的四个角都是直角；
③边：邻边垂直；
④对角线：矩形的对角线相等；
⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．
（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．
23．正方形的性质
（1）正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．
（2）正方形的性质
①正方形的四条边都相等，四个角都是直角；
②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；
③正方形具有四边形、平行四边形、矩形、菱形的一切性质．
④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．
24．四边形综合题
四边形综合题．
25．三角形的外接圆与外心
（1）外接圆：经过三角形的三个顶点的圆，叫做三角形的外接圆．
（2）外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．
（3）概念说明：
①“接”是说明三角形的顶点在圆上，或者经过三角形的三个顶点．
②锐角三角形的外心在三角形的内部；直角三角形的外心为直角三角形斜边的中点；钝角三角形的外心在三角形的外部．
③找一个三角形的外心，就是找一个三角形的三条边的垂直平分线的交点，三角形的外接圆只有一个，而一个圆的内接三角形却有无数个．
26．直线与圆的位置关系
（1）直线和圆的三种位置关系：
①相离：一条直线和圆没有公共点．
②相切：一条直线和圆只有一个公共点，叫做这条直线和圆相切，这条直线叫圆的切线，唯一的公共点叫切点．
③相交：一条直线和圆有两个公共点，此时叫做这条直线和圆相交，这条直线叫圆的割线．
（2）判断直线和圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d．
①直线l和⊙O相交⇔d＜r
②直线l和⊙O相切⇔d＝r
③直线l和⊙O相离⇔d＞r．
27．切线的性质
（1）切线的性质
①圆的切线垂直于经过切点的半径．
②经过圆心且垂直于切线的直线必经过切点．
③经过切点且垂直于切线的直线必经过圆心．
（2）切线的性质可总结如下：
如果一条直线符合下列三个条件中的任意两个，那么它一定满足第三个条件，这三个条件是：①直线过圆心；②直线过切点；③直线与圆的切线垂直．
（3）切线性质的运用
由定理可知，若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．简记作：见切点，连半径，见垂直．
28．切线的判定与性质
（1）切线的性质
①圆的切线垂直于经过切点的半径．
②经过圆心且垂直于切线的直线必经过切点．
③经过切点且垂直于切线的直线必经过圆心．
（2）切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．
（3）常见的辅助线的：
①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；
②有切线时，常常“遇到切点连圆心得半径”．
29．正多边形和圆
（1）正多边形与圆的关系
把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．
（2）正多边形的有关概念
①中心：正多边形的外接圆的圆心叫做正多边形的中心．
②正多边形的半径：外接圆的半径叫做正多边形的半径．
③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角．
④边心距：中心到正多边形的一边的距离叫做正多边形的边心距．
30．圆的综合题
圆的综合题．
31．作图—基本作图
基本作图有：
（1）作一条线段等于已知线段．
（2）作一个角等于已知角．　　（3）作已知线段的垂直平分线．　　（4）作已知角的角平分线．　　（5）过一点作已知直线的垂线．
32．作图—复杂作图
复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．
解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
33．平移的性质
（1）平移的条件
平移的方向、平移的距离
（2）平移的性质
①把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．　　②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．