北京课改版七年级上册3.8 角平分线多媒体教学ppt课件

这是一份北京课改版七年级上册3.8 角平分线多媒体教学ppt课件，共14页。PPT课件主要包含了几何的三种语言，逆定理等内容，欢迎下载使用。

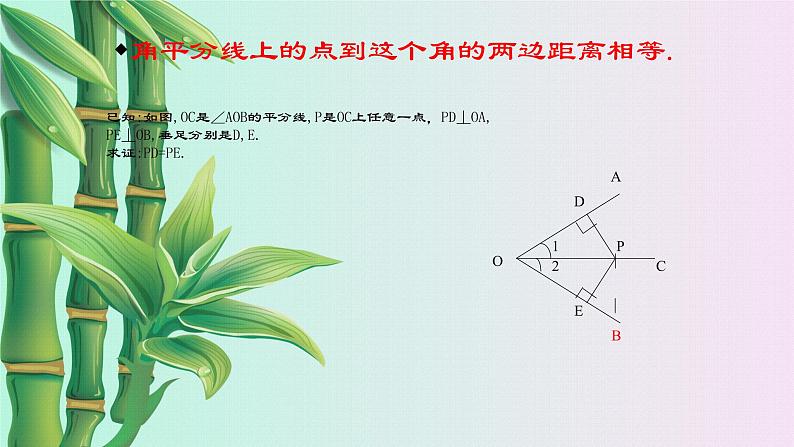
已知:如图,OC是∠AOB的平分线,P是OC上任意一点，PD⊥OA,PE⊥OB,垂足分别是D,E.求证:PD=PE.
角平分线上的点到这个角的两边距离相等.
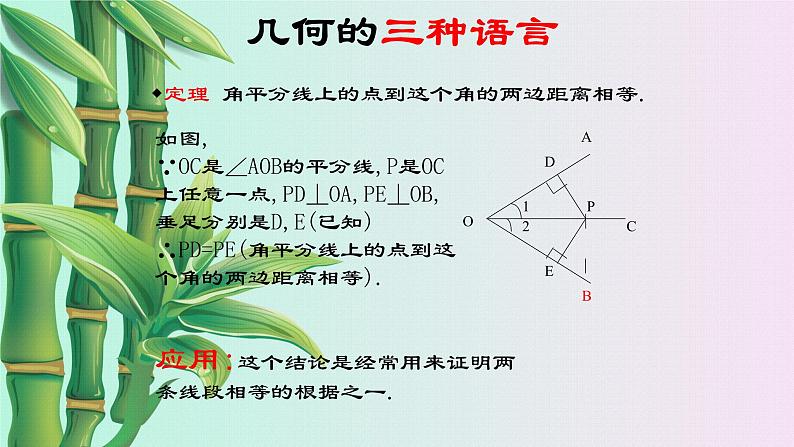
定理 角平分线上的点到这个角的两边距离相等.
应用:这个结论是经常用来证明两条线段相等的根据之一.
如图,∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)∴PD=PE(角平分线上的点到这个角的两边距离相等).
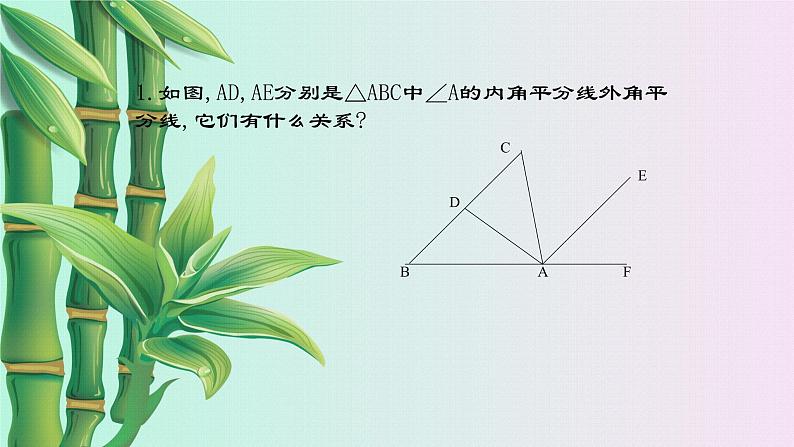
1.如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系?
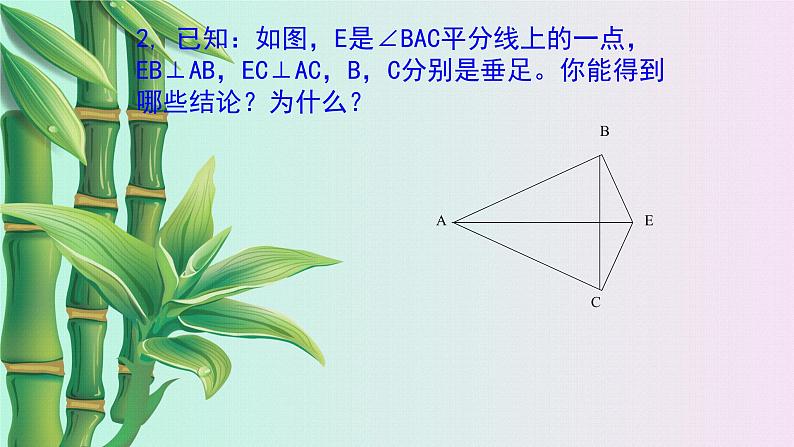
2, 已知：如图，E是∠BAC平分线上的一点，EB⊥AB，EC⊥AC，B，C分别是垂足。你能得到哪些结论？为什么？
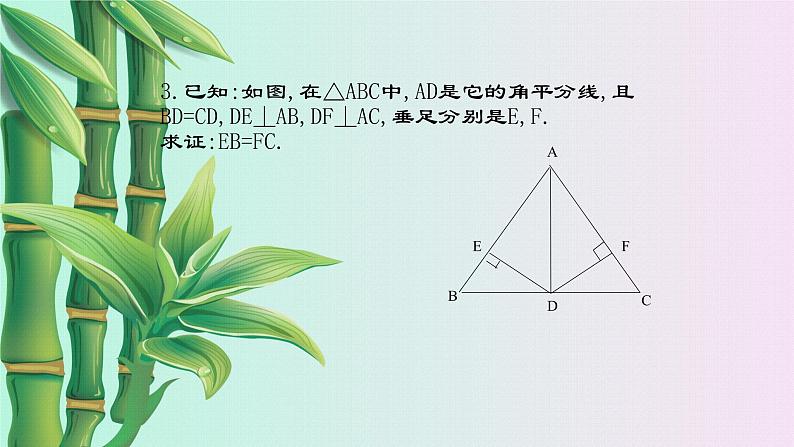
3.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.
逆命题 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
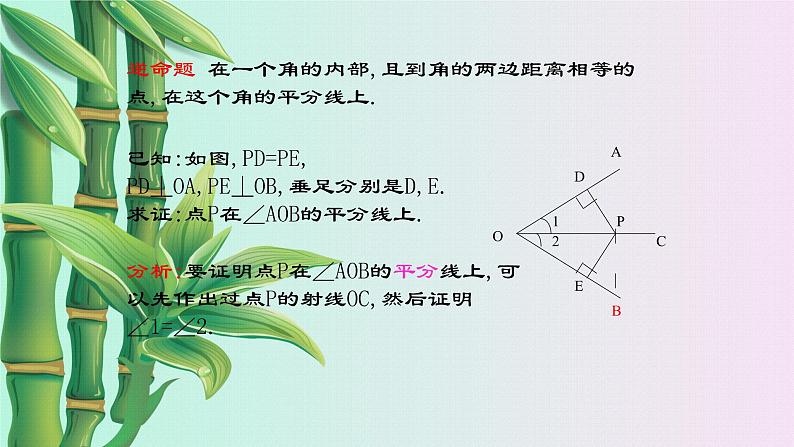
已知:如图,PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E.求证:点P在∠AOB的平分线上.
分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠1=∠2.
逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
如图,∵PA=PB, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
应用:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一。
1.已知：如图所示：PA，PC分别是⊿ABC外角∠MAC与∠NCA平分线，它们交于P，PD⊥BM于M，PF⊥BN于F.求证： 点P在∠MBN的平分线上.
2.已知：如图，P是∠ AOB平分线上的一点，PC⊥OA，PD⊥OB，垂足分别为C、D．求证：(1)OC=OD； (2)OP是CD的垂直平分线．
证明：(1)P是∠AOB角平分线上的一点，PC⊥OA，PD⊥OB∴PC=PD在Rt△OPC和Rt△OPD中，OP=OP，PC=PD，∴Rt△OPC≌Rt△OPD(HL)．∴OC=OD(全等三角形对应边相等)．
(2)又OP是∠AOB的角平分线，∴OP是CD的垂直平分线(等腰三角形“三线合一”定理)．
证明：三角形三条角平分线相交于一点．
已知：如图，设△ABC的角平分线．BM、CN相交于点P，求证：P点在∠BAC的角平分线上．
证明：过P点作PD⊥AB，PF⊥AC，PE⊥BC，其中D、E、F是垂足∵BM是△ABC的角平分线,点P在BM上∴PD=PE同理：PE=PF．∴PD=PF．∴点P在∠BAC的平分线上∴△ABC的三条角平分线相交于点P．
定理：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等．
三角形角平分线的性质定理
定理 角平分线上的点到这个角的两边距离相等.逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
三条角平分线性质定理：
三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等．