专题八 解答压轴题突破-2021年中考数学一轮复习考点突破课件

这是一份专题八 解答压轴题突破-2021年中考数学一轮复习考点突破课件，共52页。PPT课件主要包含了知识思维导图，2求AD的长等内容，欢迎下载使用。


类型1 几何变换综合题——折叠与旋转 1. （2020荆州）如图4-8-1，在矩形ABCD中，AB=20，点E是BC边上的一点，将△ABE沿着AE折叠，点B刚好落在CD边上点G处,点F在DG上，将△ADF沿着AF折叠，点D刚好落在AG上点H处，此时S△GFH∶S△AFH=2∶3.
（1）求证：△EGC∽△GFH；
（1）证明：∵四边形ABCD是矩形，∴∠B=∠D=∠C=90°.由折叠对称知,∠AGE=∠B=90°，∠AHF=∠D=90°，∴∠GHF=∠C=90°，∠EGC+∠HGF=90°，∠GFH+∠HGF=90°.∴∠EGC=∠GFH.∴△EGC∽△GFH.
（2）解：∵S△GFH∶S△AFH=2∶3，且△GFH和△AFH等高，∴GH∶AH=2∶3.∵将△ABE沿着AE折叠，点B刚好落在CD边上点G处，∴AG=AB=GH+AH=20.∴GH=8，AH=12.∴AD=AH=12.
（3）求tan∠GFH的值.
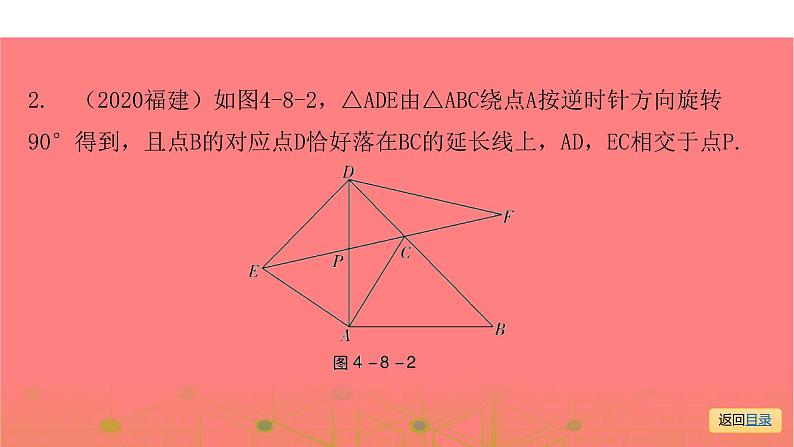
2. （2020福建）如图4-8-2，△ADE由△ABC绕点A按逆时针方向旋转90°得到，且点B的对应点D恰好落在BC的延长线上，AD，EC相交于点P.
（1）求∠BDE的度数；
（1）解：∵△ADE由△ABC绕点A按逆时针方向旋转90°得到，∴AB=AD，∠BAD=90°，△ABC≌△ADE.∴在Rt△ABD中，∠B=∠ADB=45°.∴∠ADE=∠B=45°.∴∠BDE=∠ADB+∠ADE=90°.
（2）F是EC延长线上的点，且∠CDF=∠DAC，①判断DF和PF的数量关系，并证明；
（2）①解：DF=PF.证明如下：由旋转的性质可知，AC=AE，∠CAE=90°，∴在Rt△ACE中，∠ACE=∠AEC=45°.∵∠CDF=∠DAC，∠ACE=∠ADB=45°，∴∠ADB+∠CDF=∠ACE+∠DAC，即∠FDP=∠FPD.∴DF=PF.
3. （2020菏泽）如图4-8-3，四边形ABCD的对角线AC，BD相交于点O，OA=OC，OB=OD+CD.
（1）如图①，过点A作AE∥DC交BD于点E，求证：AE=BE；
证明：（1）∵AE∥DC，∴∠CDO=∠AEO，∠EAO=∠DCO.又∵OA=OC，∴△AOE≌△COD（AAS）.∴AE=CD，OE=OD.∵OB=OE+BE，OB=OD+CD，∴BE=CD.∴AE=BE.
（2）如图②，将△ABD沿AB翻折得到△ABD′,
②若AD′∥BC，求证：CD2=2OD·BD.
（1）当0°＜α＜180°时，求证：CE=BD；
（2）如图4-8-4③，当α=90°时，延长CE交BD于点F，求证：CF垂直平分BD；
（3）在旋转过程中，求△BCD的面积的最大值，并写出此时旋转角α的度数.
类型2 点动型综合题1. （2018广东）已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如图4-8-5①，连接BC.
（1）填空：∠OBC=__________________°；（2）如图4-8-5①，连接AC，作OP⊥AC，垂足为点P，求OP的长度；
（3）如图4-8-5②，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止. 已知点M的运动速度为每秒1.5个单位长度，点N的运动速度为每秒1个单位长度，设运动时间为x s，△OMN的面积为y，则当x为何值时，y取得最大值？最大值为多少？
2. （2020青岛改编）已知：如图4-8-6，在四边形ABCD和Rt△EBF中，AB∥CD，CD＞AB，点C在EB上，∠ABC=∠EBF=90°，AB=BE=8 cm，BC=BF=6 cm，延长DC交EF于点M. 点P从点A出发，沿AC方向匀速运动，速度为2 cm/s；同时，点Q从点M出发，沿MF方向匀速运动，速度为1 cm/s. 过点P作GH⊥AB于点H，交CD于点G. 设运动时间为t（单位：s）（0＜t＜5）.
（1）当t为何值时，点M在线段CQ的垂直平分线上？
（2）连接PQ，作QN⊥AF于点N，当四边形PQNH为矩形时，求t的值；
（3）连接QC，QH，设四边形QCGH的面积为S（单位：cm2），求S与t的函数关系式.
（3）抛物线上是否存在点D，使得以点O，D，E为顶点的三角形与△BOC相似？若存在，求出m的值；若不存在，请说明理由．
类型3 线动型综合题1. （2016广东）如图4-8-7，BD是正方形ABCD的对角线，BC=2，边BC在其所在的直线上平移，将通过平移得到的线段记为PQ，连接PA，QD，并过点Q作QO⊥BD，垂足为点O，连接OA，OP.（1）请直接写出线段BC在平移过程中，四边形APQD是什么四边形；
解：（1）四边形APQD为平行四边形.
（2）请判断OA,OP之间的数量关系和位置关系，并加以证明；
（3）在平移变换过程中，设y=S△OPB，BP=x（0≤x≤2），求y与x之间的函数关系式，并求出y的最大值.
2. （2020长春改编）如图4-8-8①，在△ABC中，∠ABC=90°，AB=4，BC=3. 点P从点A出发，沿折线AB—BC以每秒5个单位长度的速度向点C运动，同时点D从点C出发，沿CA以每秒2个单位长度的速度向点A运动，点P到达点C时，点P，D同时停止运动. 当点P不与点A，C重合时，作点P关于直线AC的对称点Q，连接PQ交AC于点E，连接DP，DQ. 设点P的运动时间为t s.
（1）当点P与点B重合时，求t的值;（2）用含t的代数式表示线段EC的长;
（3）如图4-8-8②，取PD的中点M，连接QM. 当直线QM与△ABC的一条直角边平行时，直接写出t的值.
类型4 形动型综合题1. （2020深圳）如图4-8-9①，抛物线y=ax2+bx+3（a≠0）与x轴的交点为A（-3，0）和B（1，0），与y轴交于点C，顶点为点D.
（1）求该抛物线的解析式；
（2）连接AD，DC，CB，将△OBC沿x轴以每秒1个单位长度的速度向左平移，得到△O′B′C′，点O,B,C的对应点分别为点O′,B′,C′，设平移时间为t s，当点O′与点A重合时停止移动,记△O′B′C′与四边形AOCD重合部分的面积为S，请直接写出S与t之间的函数关系式；
2. 已知：如图4-8-10①，在平行四边形ABCD中，AB=3 cm，BC=5 cm，AC⊥AB，△ACD沿AC的方向以1 cm/s的速度匀速平移得到△PNM;同时,点Q从点C出发，沿着CB方向匀速移动，速度为1 cm/s，当△PNM停止平移时，点Q也停止移动，如图4-8-10②，设移动时间为t（单位：s）（0＜t＜4）, 连接PQ，MQ，MC.
（1）当t为何值时，PQ∥AB？
（2）当t=3时，求△QMC的面积；
（3）是否存在t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由.