浙江省宁波市奉化区2020-2021学年七年级下学期期末数学试题（word版 含答案）

2020学年第二学期期末抽测七年级数学试题

考生须知：

1.全卷有三大题，24个小题、满分为120分，考试时间为100分钟.

2.请将姓名、准考证号分别填写在答题卷的规定位置上.

3.答题时，请将试题答案书写在答题卷上规定区域.试题卷上书写或答题卷上规定区域外书写的答案均无效.

4.不允许使用计算器，没有近似计算要求的试题，结果都不能用近似数表示.

一、选择题（每小题3分，共30分，每小题给出的四个选项中只有一项符合题 目要求）

1.下列图案中，能通过平移得到如图的图案是（  ）

A．         B． C．      D．

2.下面调查统计中，适合采用普查方式的是（  ）

A．华为手机的市场占有率

B．乘坐飞机的旅客是否携带了违禁物品

C．“国家宝藏”专栏电视节目的收视率

D．“现代”汽车每百公里的耗油量

3.我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了米.用科学记数法表示为（  ）

A．           B．    C．      D．

4.下列计算正确的是（  ）

A．          B．  C．    D．

5.若是关于，的二元一次方程的一组解，则的值为（  ）

A．           B．         C．         D．

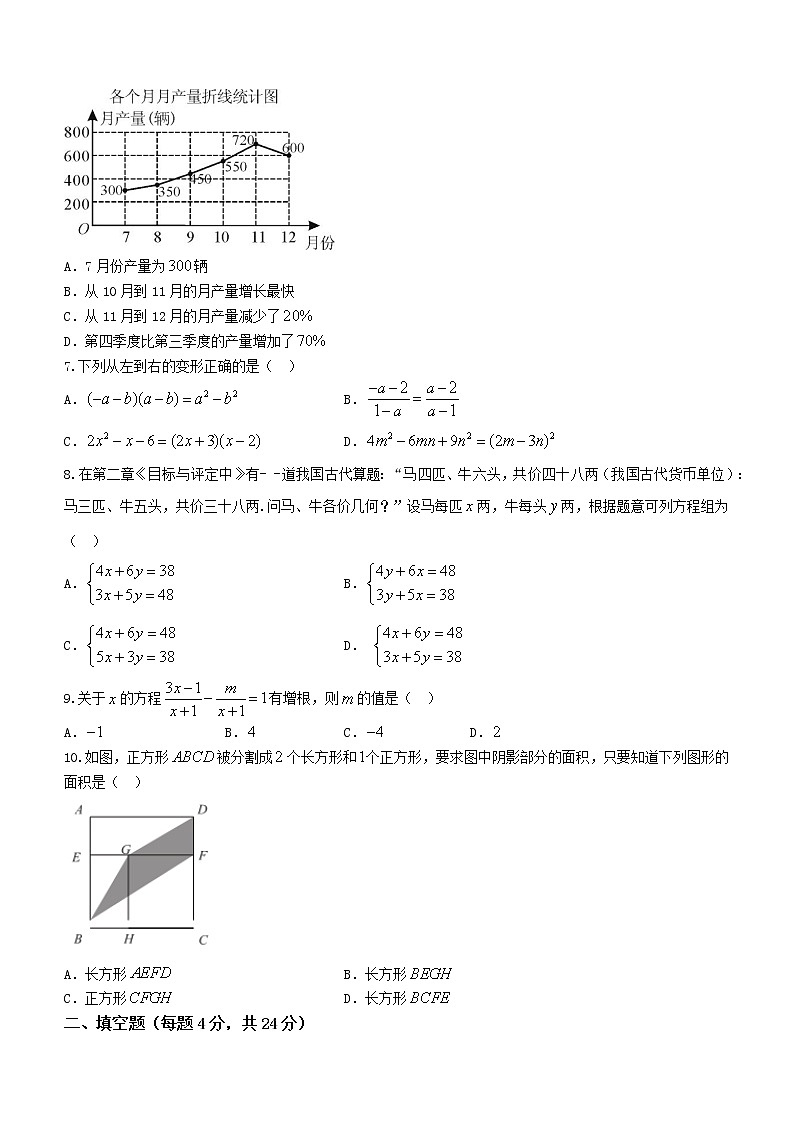
6.某电动车厂2020年第三、四季度各月产量情况如图所示.则下列说法错误的是（  ）

A．7月份产量为辆

B．从10月到11月的月产量增长最快

C．从11月到12月的月产量减少了

D．第四季度比第三季度的产量增加了

7.下列从左到右的变形正确的是（  ）

A．           B．

C．        D．

8.在第二章《目标与评定中》有- -道我国古代算题：“马四匹、牛六头，共价四十八两（我国古代货币单位）：马三匹、牛五头，共价三十八两.问马、牛各价几何？”设马每匹两，牛每头两，根据题意可列方程组为（  ）

A．          B．

C．         D．

9.关于的方程有增根，则的值是（  ）

A．           B．         C．         D．

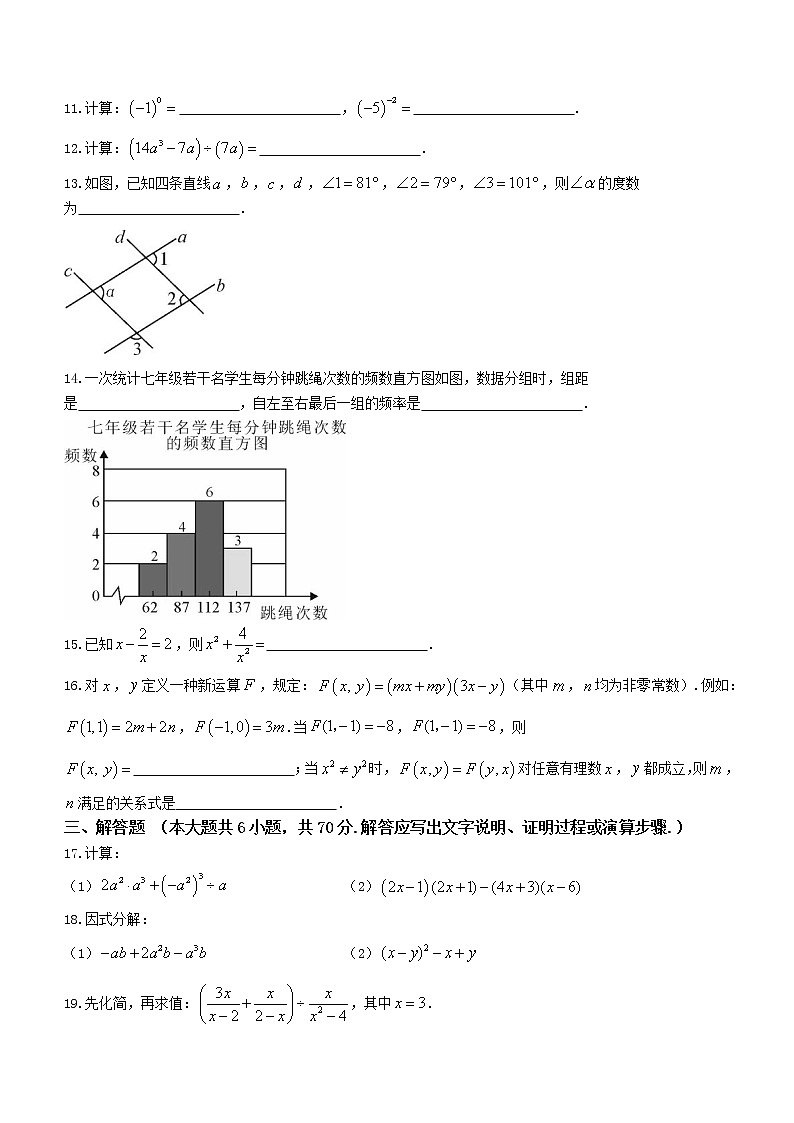
10.如图，正方形被分割成个长方形和个正方形，要求图中阴影部分的面积，只要知道下列图形的面积是（  ）

A．长方形  B．长方形

C．正方形        D．长方形

二、填空题（每题4分，共24分）

11.计算：                       ，                       .

12.计算：                       ．

13.如图，已知四条直线，，，，，，，则的度数为                       ．

14.一次统计七年级若干名学生每分钟跳绳次数的频数直方图如图，数据分组时，组距是                       ，自左至右最后一组的频率是                       ．

15.已知，则                       ．

16.对，定义一种新运算，规定：（其中，均为非零常数）.例如：，.当，，则                       ；当时，对任意有理数，都成立，则，满足的关系式是                       ．

三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

17.计算：

（1）  （2）

18.因式分解：

（1）  （2）

19.先化简，再求值：，其中.

20.解方程（组）：

（1）  （2）

21.某校学生会调查了七年级部分学生对“垃圾分类”的了解程度.

（1）在确定调查方式时，学生会设计了以下三种方案，其中最具有代表性的方案是                       ；

方案①：调查七年级部分男生；

方案②：调查七年级部分女生；

方案③：到年级每个班去随机调查一定数量的学生；

（2）学生会采用最具有代表性的方案进行调查后，将收集到的数据绘制成如下两幅不完整的统计图（如图1、图2），请你根据图中信息，回答下列问题：

图1                              图2

①本次调查学生人数共有                       名；

②补全图1中的条形统计图，图2中“了解一点”的圆心角度数为                       ；

③根据本次调查估计该校八年级名学生中，比较了解“垃圾分类”的学生大约有多少名.

22.如图，已知，，.

（1）与平行吗？请说明理由.

（2）若与互补，求的度数.

23.某生态柑橘园现有柑橘吨，租用辆和两种型号的货车将柑橘一次性运往外地销售.已知每辆车满载时，型货车的总费用元，型货车的总费用元，每辆型货车的运费是每辆型货车的运费的倍.

（1）每辆型货车和型货车的运费各多少元？

（2）若每辆车满载时，租用辆型车和辆型车也能一次性将柑橘运往外地销售，则每辆型货车和型车货各运多少吨？

24.阅读理解并解答：

【方法呈现】

（1）我们把多项式及叫做完全平方式.在运用完全平方公式进行因式分解时，关键是判断这个多项式是不是一个完全平方式，同样地，把一个多项式进行局部因式分解可以来解决代数式值的最小（ 或最大）问题.

例如：，

，

.

则这个代数式的最小值是                       ，这时相应的的值是                       .

【尝试应用】

（2）求代数式的最小（或最大）值，并写出相应的的值.

【拓展提高】

（3）将一根长的铁丝剪成两段，并以每一段铁丝的长度为周长各做成-一个正方形，则这两个正方形面积之和有最小（或最大）值？若有，求此时这根铁丝剪成两段后的长度及这两个正方形面积的和；若没有，请说明理由.

试卷答案

一、选择题

1-5：         6-10：

二、填空题

11.， 12.  13.          14.，

15.            16.，

三、解答题

17.（1）原式

（2）原式

18.（1）原式

（2）原式

19.原式

当时，原式.

20.（1）

（2）两边都乘以，得：，

解得：，经检验：分式方程的解为.

21.（1）方案③

（2）①

②补图略；.

③.

22.（1）.理由如下：

，.

（在同一平面内，垂直于同一条直线的两条直线互相平行）

（2），

，

与互补，

与互补，

，

，

，

.

23.（1）设每辆型货车运费为元，

由题意得：，解得：.

经检验：是原方程的解且符合题意，.

答：每辆型货车运费元，型货车的运费元.

（2）设每辆型货车运吨，型货车运吨，

由题意得：，解得，

答：设每辆型货车运吨， 型货车运吨.

24.（1），.

（2）

则这个代数式的最大值是，这时相应的的值是.

（3）设一段铁丝长为，则另一段长为，由题意得：

当，两个正方形的面积之和有最大值.