


初中北京课改版12.2 三角形的性质集体备课课件ppt
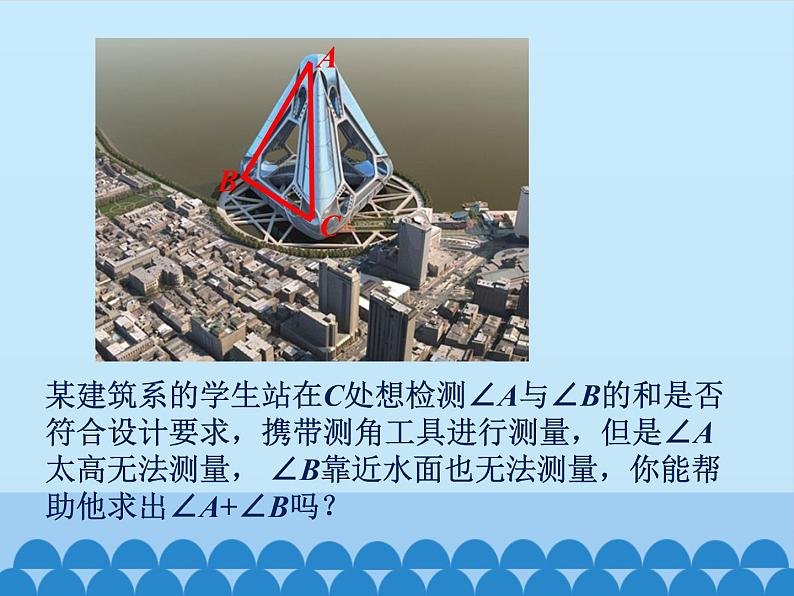
展开某建筑系的学生站在C处想检测∠A与∠B的和是否符合设计要求,携带测角工具进行测量,但是∠A太高无法测量, ∠B靠近水面也无法测量,你能帮助他求出∠A+∠B吗?
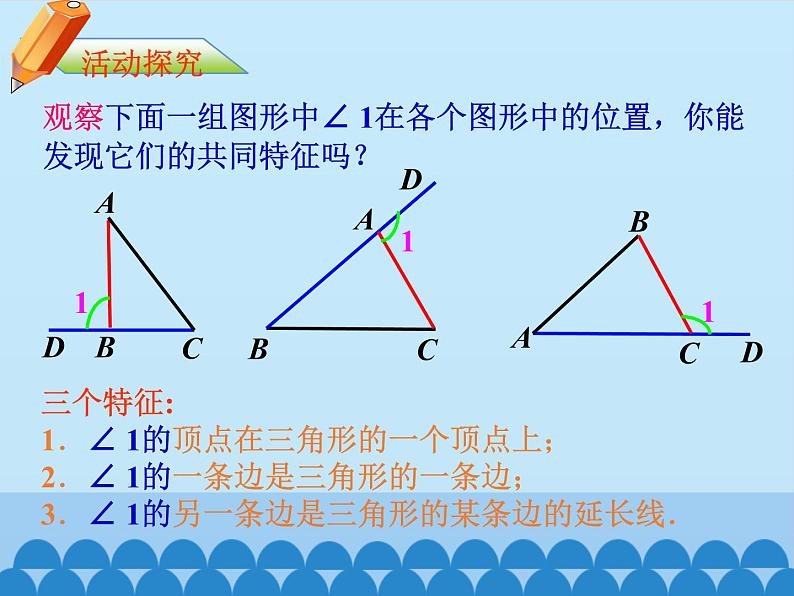
观察下面一组图形中∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
三个特征:1.∠ 1的顶点在三角形的一个顶点上;2.∠ 1的一条边是三角形的一条边;3.∠ 1的另一条边是三角形的某条边的延长线.
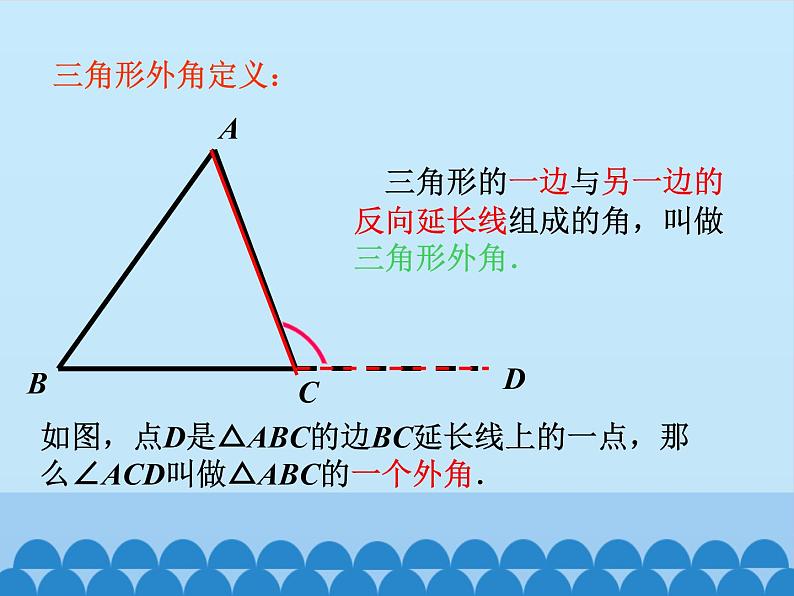
三角形的一边与另一边的反向延长线组成的角,叫做三角形外角.
如图,点D是△ABC的边BC延长线上的一点,那么∠ACD叫做△ABC的一个外角.
想一想:1、每一个三角形有几个外角?2、每一个顶点处相对应的外角有几个?3、这些外角中有几个外角相等? 4、三角形的每一个外角与三角形的三个内角有什么位置关系?
画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.
1、每一个三角形都有6个外角;
2、每一个顶点相对应的外角都有2个;
4、一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
3、这6个外角中有3个外角相等.
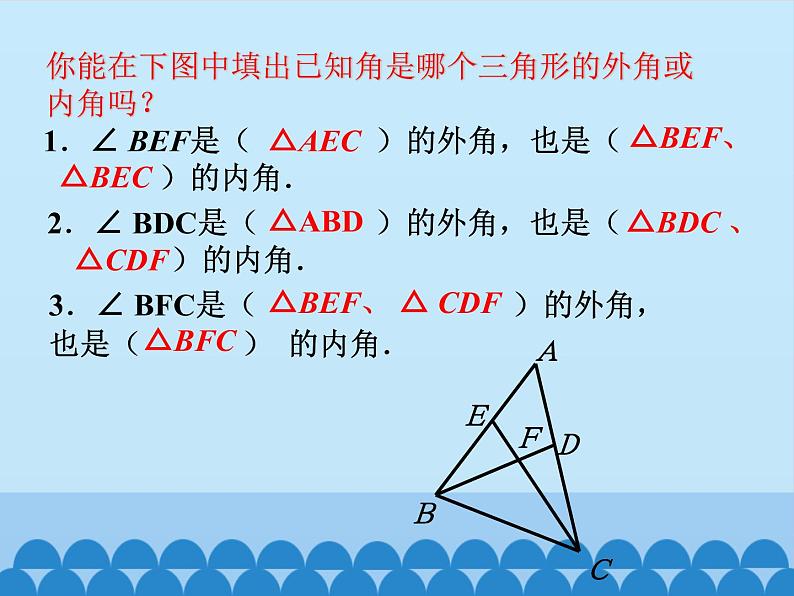
你能在下图中填出已知角是哪个三角形的外角或内角吗?
1.∠ BEF是( )的外角,也是( )的内角.
2.∠ BDC是( )的外角,也是( )的内角.
3.∠ BFC是( )的外角,也是( ) 的内角.
△BEF、 △ CDF
三角形的外角与内角的关系:
如图△ABC中,则 ∠ACB+∠ACD=180°,
结论: 三角形的外角与它相邻的内角互为邻补角.
即三角形的外角与它 相邻内角的和为180°.
△ABC的外角∠ACD与它不相邻的内角∠ A、 ∠ B有怎样的关系?
∠ACD= ∠ A+ ∠ B.
证明: △ABC中,∵∠A+∠B+∠ACB=180°(三角形内角和定理),∠ACD+∠ACB=180°(平角定义),∴∠ACD=∠A+∠B(等量代换).
你还能其他方法加以证明吗?
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
推论1:三角形的一个外角等于与它不相邻的两个内角的和.
推论2:三角形的一个外角大于任何一个与它不相邻的内角.
例3 如图,点B,C,D,E是同一直线上的四点,∠B=∠BAC=30°,∠CAD=60°.求∠ADE的度数.
解:∵∠B=∠BAC=30°,
∴∠ADE=∠ACD+∠CAD(三角形内角和定理的推论1)
=30°+30°=60°.
又∵∠CAD=60°(已知),
∴∠ACD=∠B+∠BAC(三角形内角和定理的推论1)
=60°+60°=120°.
即∠ADE=120°.
如图,线段AB,CD,EF两两交于点G,P,H.怎样求∠A+∠B+∠C+∠D+∠E+∠F的度数?
解:∵∠AGP=∠A+∠C,∠EHG=∠B+∠E,∠DPH=∠D+∠F,(三角形内角和定理的推论1)
∠AGP+∠HGP=180°,∠EHG+∠GHP=180°,∠DPH+∠HPG=180°,
∴∠AGP+∠HGP+∠EHG+∠GHP+∠DPH+∠HPG=540°,
∵∠HGP+∠GHP+∠HPG=180°,(三角形内角和定理)
∴∠AGP+∠EHG+∠DPH=360°,
即∠A+∠B+∠C+∠D+∠E+∠F=360°.
1.三角形的内角中最多能有几个直角?为什么?
2.三角形的内角中最多能有几个钝角?为什么?
三个角都是锐角的三角形叫做锐角三角形;
有一个角是钝角的三角形叫做钝角三角形.
有一个角是直角的三角形叫做直角三角形;
三角形按角的大小可以分成:
如果个三角形有两个锐角互余,你能判定这个三角形的形状吗?为什么?
直角三角形的判定方法:
有两个锐角互余的三角形是直角三角形.
2.三角形的分类(按角分).
1.直角三角形内角和定理的推论:
3.直角三角形的判定方法:
1.求各图中∠1的度数.
2.如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:(1)∠B的度数;(2)∠C的度数.
问:(1)中为什么∠ADC=∠B+∠BAD?(2)中求∠C的度数还有其他方法吗?
3.一个零件的形状如图所示,按规定∠BAC=90°, ∠B=21°, ∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学的知识说出其中的道理吗?
初中数学北京课改版九年级上册18.6 相似三角形的性质优秀ppt课件: 这是一份初中数学北京课改版九年级上册18.6 相似三角形的性质优秀ppt课件,共20页。PPT课件主要包含了情境引入,三条边的长度,三个内角的度数,面积等等,探究归纳,对应边的比,相似比k,对应高的比,对应中线的比,对应角平分线的比等内容,欢迎下载使用。
初中数学北京课改版八年级上册12.6 等腰三角形精品ppt课件: 这是一份初中数学北京课改版八年级上册12.6 等腰三角形精品ppt课件,共10页。PPT课件主要包含了BDCD,AD平分∠BAC等内容,欢迎下载使用。
初中数学北京课改版八年级上册12.11 勾股定理优质ppt课件: 这是一份初中数学北京课改版八年级上册12.11 勾股定理优质ppt课件,共1页。













