浙江省温州市乐清市中考数学适应性试卷Word版.doc

2021年浙江省温州市乐清市中考数学适应性试卷

一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1．计算：4×（﹣3）的结果是（　　）

A．1 B．﹣1 C．12 D．﹣12

2．据国家航天局介绍，受天体运动规律影响，火星与地球距离在0.5亿公里至4亿多公里之间变化．天问一号探测器到达火星附近时，距离地球约190 000 000公里，其中数据190 000 000用科学记数法表示为（　　）

A．0.19×109 B．1.9×108 C．19×107 D．1.9×107

3．如图所示的几何体是由两个长方体组成的，它的俯视图是（　　）

A． B． C． D．

4．一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是红球的概率为（　　）

A． B． C． D．

5．对某校的学生关于“垃圾分类知多少”的情况进行抽样问卷调查后（每人选一种），绘制成如图所示统计图．已知选择“非常了解”的有60人，那么选择“基本了解”的有（　　）

A．20 B．40 C．60 D．80

6．若关于x的方程x2﹣2x+m＝0有实数根，则m的值可以是（　　）

A．1 B．2 C．3 D．4

7．已知一个扇形的圆心角为120°，半径为4，则该扇形的弧长为（　　）

A．2π B．π C．3π D．π

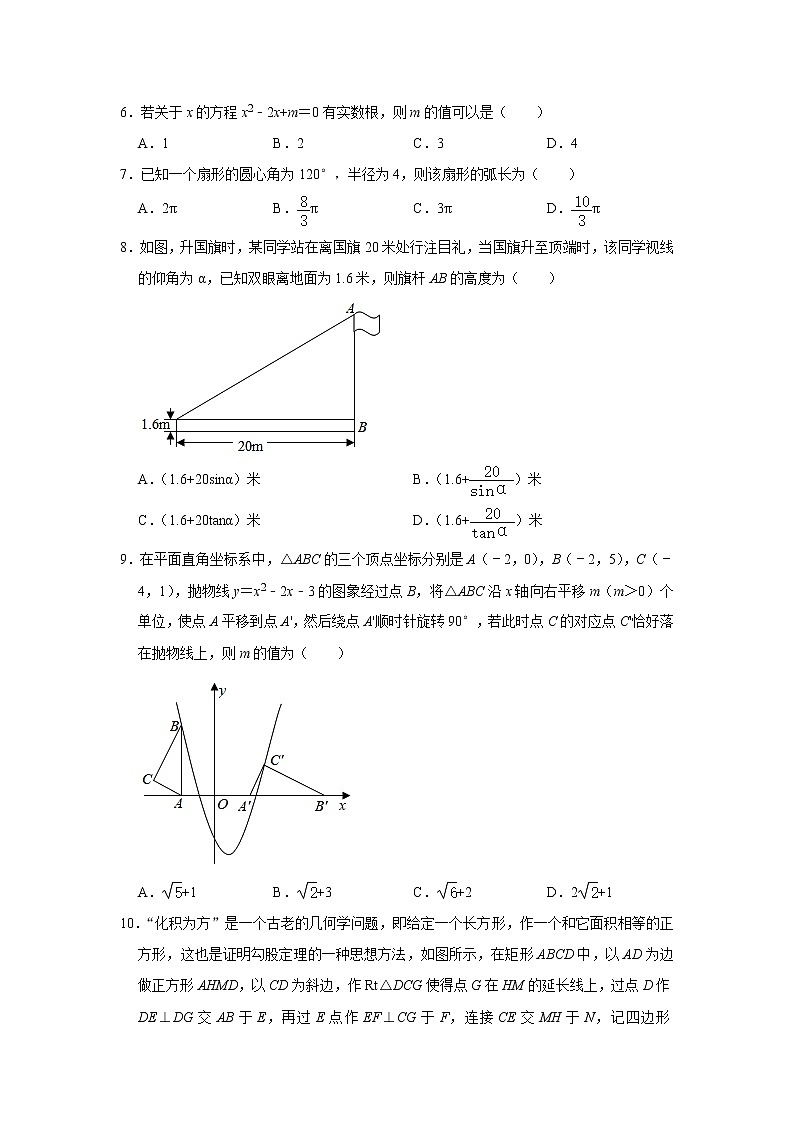
8．如图，升国旗时，某同学站在离国旗20米处行注目礼，当国旗升至顶端时，该同学视线的仰角为α，已知双眼离地面为1.6米，则旗杆AB的高度为（　　）

A．（1.6+20sinα）米 B．（1.6+）米 

C．（1.6+20tanα）米 D．（1.6+）米

9．在平面直角坐标系中，△ABC的三个顶点坐标分别是A（﹣2，0），B（﹣2，5），C（﹣4，1），抛物线y＝x2﹣2x﹣3的图象经过点B，将△ABC沿x轴向右平移m（m＞0）个单位，使点A平移到点A'，然后绕点A'顺时针旋转90°，若此时点C的对应点C'恰好落在抛物线上，则m的值为（　　）

A．+1 B．+3 C．+2 D．2+1

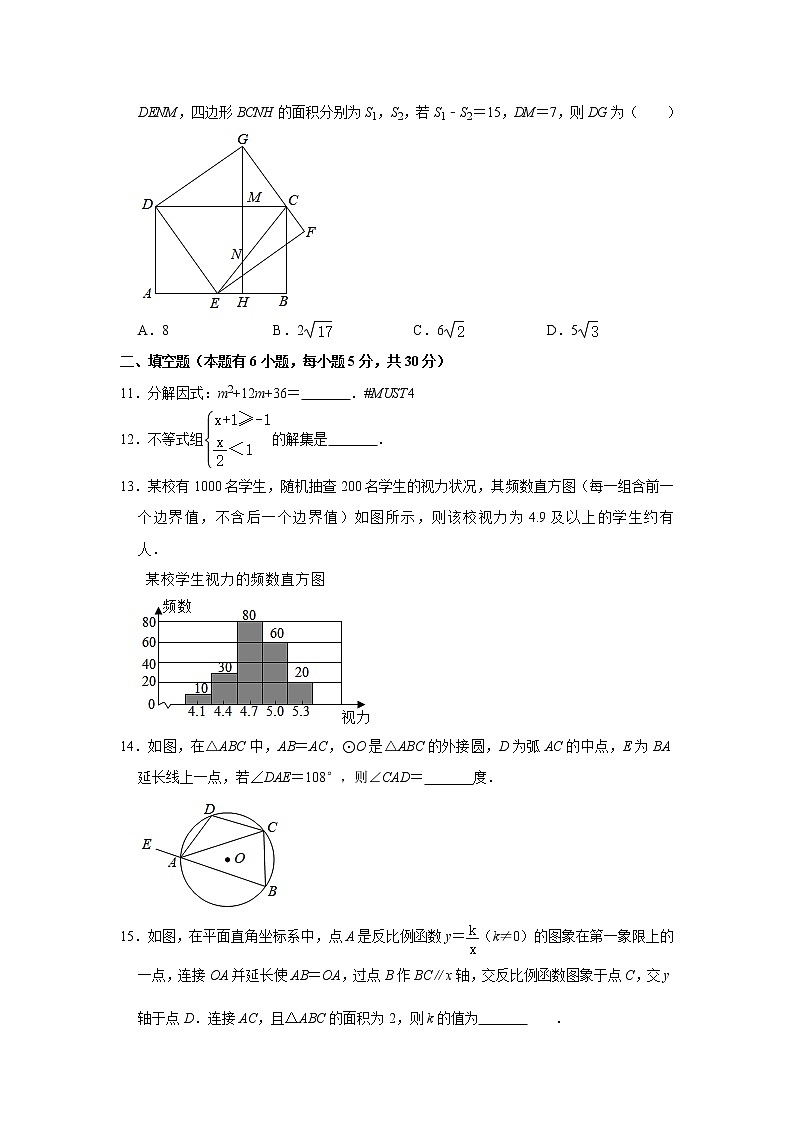
10．“化积为方”是一个古老的几何学问题，即给定一个长方形，作一个和它面积相等的正方形，这也是证明勾股定理的一种思想方法，如图所示，在矩形ABCD中，以AD为边做正方形AHMD，以CD为斜边，作Rt△DCG使得点G在HM的延长线上，过点D作DE⊥DG交AB于E，再过E点作EF⊥CG于F，连接CE交MH于N，记四边形DENM，四边形BCNH的面积分别为S1，S2，若S1﹣S2＝15，DM＝7，则DG为（　　）

A．8 B．2 C．6 D．5

二、填空题（本题有6小题，每小题5分，共30分）

11．分解因式：m2+12m+36＝　   　．#MUST4

12．不等式组的解集是　   　．

13．某校有1000名学生，随机抽查200名学生的视力状况，其频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，则该校视力为4.9及以上的学生约有　   　人．

14．如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，D为弧AC的中点，E为BA延长线上一点，若∠DAE＝108°，则∠CAD＝　   　度．

15．如图，在平面直角坐标系中，点A是反比例函数y＝（k≠0）的图象在第一象限上的一点，连接OA并延长使AB＝OA，过点B作BC∥x轴，交反比例函数图象于点C，交y轴于点D．连接AC，且△ABC的面积为2，则k的值为　   　．

16．随着“科学运动、健康生活”的理念深入人心，跑步机已成为家居新宠，某品牌跑步机（如图1）的跑道可以旋转（如图2），图3为跑道CD绕D点旋转到DC位置时的主视图，其中AE为显示屏，AF为扶手，点C在直线AE上，GH为可伸缩液压支撑杆，G，H的位置不变，GH的长度可变化，已知AB＝100cm，cosB＝，∠EAB+∠B＝180°，则BC＝　   　cm．若BG＝50cm，GH∥AB，∠B＝2∠DHG，且A，H，C恰好在同一直线上，则AD＝　   　cm．

三、解答题（本题有8小题，共80分，解答需写出必要的文字说明、演算步骤或证明过程）

17．（1）计算：|﹣8|﹣﹣（﹣1）0+（﹣5）．

（2）化简：+．

18．如图，在△ABC中，AB＝AC，AD是BC边上的中线，E是AC边上一点，过点D作DE⊥DF交CA的延长线于点F，DB＝DF．

（1）求证：△ABD≌△EFD．

（2）若∠B＝30°，AB＝6，求AF的长．

19．某班为了解班级同学寒假期间在家进行体育锻炼的情况，通过钉钉线上运动打卡活动，统计了班级40名同学一段时间的运动打卡次数如表：

（1）求这40名同学打卡次数的平均数．

（2）为了调动大多数同学锻炼的积极性，班主任准备制定一个打卡奖励标准，凡打卡次数达到或超过这个标准的同学将获得奖励的措施．如果你是班主任，从平均数、中位数、众数的角度进行分析，你将如何确定这个“打卡奖励”标准？

20．如图，在6×6的方格纸中，每个小正方形的边长为1，每个小正方形的顶点称为格点，请按要求画出格点三角形与格点四边形．

（1）在图1中以线段AB为边画一个格点△ABC，使AB＝BC．

（2）在图2中以线段AB为边画一个格点四边形ABCD，使其面积为7，且∠BAD＝90°．

21．如图，在△ABC中，∠ACB＝90°，以BC为直径作⊙O交AB交于点D，作切线DE交AC于点E，过点B作BF⊥ED，交ED的延长线于点F，交⊙O于点G，连接CG交AB于点H．

（1）求证：AE＝EC；

（2）若AB＝16，GH＝DF，求BC的长．

22．在新冠肺炎防疫工作中，某学校从商店购买测温枪和洗手液，已知测温枪的单价比洗手液单价多35元，若用2800元购买测温枪的数量与用840元购买洗手液的数量相同．

（1）求测温枪与洗手液的单价各是多少元？

（2）若该学校决定购进测温枪与洗手液数量共200件，考虑到实际需求，要求购进洗手液的数量不超过测温枪的数量的6倍，求该学校购买费用最少是多少元？

（3）该学校还需要购买口罩，口罩的单价每包10元，若用5200元购买测温枪、洗手液与口罩这三种防疫用品，其中测温枪与洗手液的数量之比为1：8，则该校至少可以购买这三种防疫用品共多少件？

23．已知抛物线y＝x2+bx+c的对称轴为直线x＝1，图象与x轴交于点（4，0）．

（1）求抛物线的函数表达式．

（2）若（5，y1）和（m，y2）为抛物线上不同的两点，当y2＞y1时，求出m的取值范围．

（3）若把抛物线的图象沿x轴平移n个单位，在自变量x的值满足2≤x≤3的情况下，与其对应的函数值y的最小值为﹣3，求n的值．

24．如图，在四边形ABCD中，∠B＝∠C＝90°，AB＝BC＝12，点E是BC上一点，BE＝4，EA平分∠BED，EF⊥DE交AB于F，动点P在DE上从点D向终点E匀速运动，同时，动点Q在AB上从点B向终点A匀速运动，它们同时到达终点，PQ与AE交于点G．

（1）求证：AF＝EF；

（2）求AD的长；

（3）①当PQ与四边形AFED的一边平行时，求所有满足条件的BQ的长；

②当PQ⊥AE时，PQ交CD于M，记△AQG，△PEG，△PDM的面积分别为S1，S2，S3，请直接写出此时S1：S2：S3的值．