安徽省蚌埠二中2021届高三下学期6月最后一卷数学文科试题+答案

蚌埠二中2021届高三最后一卷

数学（文科）试题

（试卷满分值：150分    考试时间：120分钟）

注意事项：

第Ⅰ卷所有选择题的答案必须用2B铅笔涂在答题卡中相应的位置、第Ⅱ卷的答案必须用0.5毫米黑色签字笔写在答题卡的相应位置上，否则不予计分.

第Ⅰ卷（选择题    共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1.设（为虚数单位），则

A.0                   B.                    C.1                    D.

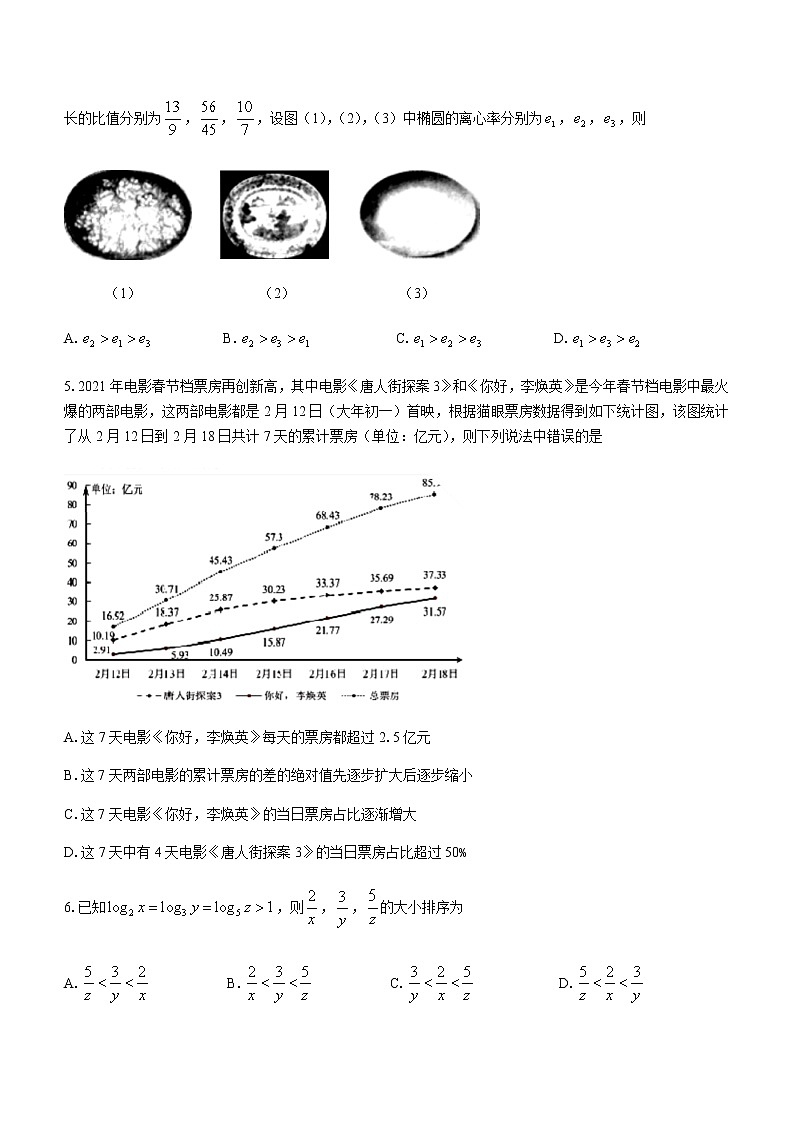
2.七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形，一块中三角形和两块全等的大三角形），一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形，若向正方形内随机抛掷2000粒绿豆（大小忽略不计），则落在图中阴影部分内绿豆粒数大约为

A.750                 B.500                   C.375                   D.250

3.集合，，则

A.           B.               C.             D.

4.明朝的一个葡萄纹椭圆盘如图（1）所示，清朝的一个青花山水楼阁纹饰椭圆盘如图（2）所示，北宋的一个汝窑椭圆盘如图（3）所示，这三个椭圆盘的外轮廓均为椭圆.已知图（1），（2），（3）中椭圆的长轴长与短轴长的比值分别为，，，设图（1），（2），（3）中椭圆的离心率分别为，，，则

（1）                 （2）               （3）

A.          B.            C.          D.

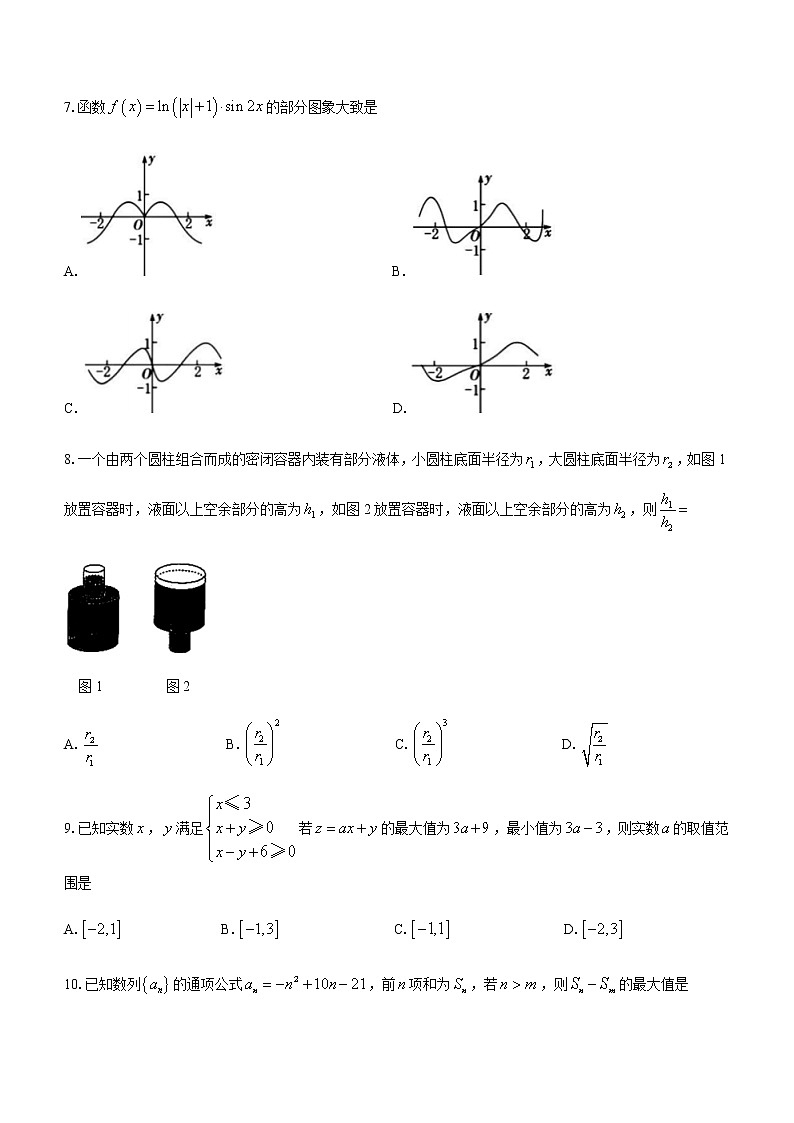
5.2021年电影春节档票房再创新高，其中电影《唐人街探案3》和《你好，李焕英》是今年春节档电影中最火爆的两部电影，这两部电影都是2月12日（大年初一）首映，根据猫眼票房数据得到如下统计图，该图统计了从2月12日到2月18日共计7天的累计票房（单位：亿元），则下列说法中错误的是

A.这7天电影《你好，李焕英》每天的票房都超过2.5亿元

B.这7天两部电影的累计票房的差的绝对值先逐步扩大后逐步缩小

C.这7天电影《你好，李焕英》的当日票房占比逐渐增大

D.这7天中有4天电影《唐人街探案3》的当日票房占比超过50%

6.已知，则，，的大小排序为

A.           B.           C.            D.

7.函数的部分图象大致是

A.                         B.

C.                        D.

8.一个由两个圆柱组合而成的密闭容器内装有部分液体，小圆柱底面半径为，大圆柱底面半径为，如图1放置容器时，液面以上空余部分的高为，如图2放置容器时，液面以上空余部分的高为，则

图1         图2

A.                  B.                C.                D.

9.已知实数，满足若的最大值为，最小值为，则实数的取值范围是

A.              B.                C.                D.

10.已知数列的通项公式，前项和为，若，则的最大值是

A.5                   B.10                    C.15                    D.20

11.已知函数，将的图象向右平移个单位得到函数的图象，点，，是与图象的连续相邻的三个交点，若是钝角三角形，则的取值范围是

A.         B.          C.            D.

12.函数的零点个数为

A.8                   B.9                     C.6                     D.4

第Ⅱ卷（非选择题    共90分）

二、填空题（本大题共4小题，每小题5分，共20分.）

13.已知，则___________.

14.根据记载，最早发现勾股定理的人应是我国西周时期的数学家商高，商高曾经和周公讨论过“勾三股四弦五”的问题.现有满足“勾三股四弦五”，其中“股”，为“弦”上一点（不含端点），且满足勾股定理，则___________.

15.我国古代有一种容器叫“方斗”，“方斗”的形状是一种上大下小的正四棱台（两个底面都是正方形的四棱台），如果一个方斗的容积为28升（一升为一立方分米），上底边长为4分米，下底边长为2分米，则该方斗的外接球的表面积为___________平方分米.

16.设双曲线：的左、右焦点分别为，，过的直线与双曲线的右支交于两点，，若，且是的一个四等分点，则双曲线的离心率是___________.

三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.）

（一）必考题：（每小题12分，共60分.）

17.已知内接于单位圆，且.

（1）求角；

（2）求面积的最大值.

18.自从新型冠状病毒爆发以来，美国疫情持续升级，以下是美国2020年4月9日-12月14日每隔25天统计1次共计11次累计确诊人数（万）.

（1）将4月9日作为第1次统计，若将统计时间序号作为变量，每次累计确诊人数作为变量，得到函数关系，对上表的数据作初步处理，得到部分数据已作近似处理的一些统计量的值，，，，，，，，，根据相关数据，确定该函数关系式（参数，的取值精确到0.01）；

（2）为了了解患新冠肺炎与年龄的关系，已知某地曾患新冠肺炎的老年、中年、青年的人数分别为45人，30人，15人，按分层抽样的方法随机抽取6人进行问卷调查，再从6人中随机抽取2人进行调查结果对比，求这2人中至少有一人是老年人的概率.

参考公式：线性回归方程中，，；

19.如图，在直四棱柱中，底面四边形为梯形，点为上一点，且，，.

（1）求证：平面；

（2）求点到平面的距离.

20.已知抛物线：的焦点为，直线：与抛物线交于，两点.

（1）若直线过焦点，且与圆交于，（其中，在y轴同侧）两点，求证：是定值；

（2）设抛物线在点和点处的切线交于点，试问在轴上是否存在点，使得四边形为菱形？若存在，求出此时直线的斜率和点的坐标；若不存在，请说明理由.

21.函数.

（1）求在xe处的切线方程（为自然对数的底数）；

（2）设，若，且，满足，求证：.

（二）选考题（共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分）

22.【选修4-4：坐标系与参数方程】

在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴的正半轴为极轴，取相同长度单位建立极坐标系，直线的极坐标方程为.

（1）求曲线的普通方程和极坐标方程；

（2）设射线：与曲线交于点，与直线交于点，求线段的长.

23.【选修4-5：不等式选讲】

已知函数，记的最小值为.

（1）解不等式的解集；

（2）是否存在正实数，，同时满足：，说明理由.

蚌埠二中2021届高三最后一卷

数学（文科）参考答案

一、选择题：（每小题5分，共60分）

1.C    2.C    3.A    4.D    5.D    6.A    7.B    8.B    9.C    10.B    11.D    12.A

二、填空题：（每小题5分，共20分）

13.    14.    15.    16.

三、解答题：

（一）必考题：（每小题12分，共60分）

17.（1）∵，∴，

∴，

∵

∴.

（2）的外接圆为单位圆，∴其半径，由正弦定理可得，由余弦定理可得，代入数据可得，当且仅当时，“=”成立，∴，∴的面积，

面积的最大值为.

18.（1）因为，所以，

由已知得，

，，

∴所求函数方程为．

（2）从90人中按照分层抽样的方法随机抽取6人，

老年、中年、青年分别抽取的人数为3人，2人，1人，

记3个老年人为，，，2个中年人为，，1个青年人为，

抽取的全部结果为，，，，，，，，，，，，，，共15种．

至少1人是老年人的有，，，，，，，，，，，，共12种．

所以至少1人是老年人的概率为．

19.（1）因为四棱柱为直四棱柱，所以，

又已知，所以点为的中点，

又，且，所以且，所以四边形为平行四边形，所以，

又在平面中，，在平面中，，由面面平行的判定定理可以证明平面平面，又平面，所以平面

（2）由（1）知点为的中点，

又在梯形中，，

所以为等边三角形，所以，

又，所以，

所以的面积，

则，

又在中，，

又在，由余弦定理得，

所以的面积为

，

设点到平面的距离为，由等体积法有，

则，即，解得，

故所求点到平面的距离为.

20.抛物线：的焦点，

设，，联立与有，

则，且，．

（Ⅰ）若直线过焦点，则，则，．

由条件可知圆圆心为，半径为1，

由抛物线的定义有，，则，，

，

（或）

即为定值，定值为1．

（Ⅱ）当直线的斜率为0，且时为菱形．理由如下：

由有，则，

则抛物线在处的切线为，

即……①

同理抛物线在处的切线为……②

联立①②解得，代入①式解得，即．

又，所以，

即的中点为．

则有轴．若为菱形，则，所以，

此时，，则．

方法二：

设，，，由有，则，

若为菱形，则，，则，，

即，，

则，∴，

∴，，

则抛物线在处的切线为，即……①

同理抛物线在处的切线为……②

联立①②．

又的中点为，所以．

方法三：

设，，，由有，则，

若为菱形，则，，

则，即，

则，∴，

此时直线：，则

所以．

21.（1），，则，

故在处的切线方程为

即；

（2）证明：由题可得，，

当时，，则；

当时，，则，

所以，当时，，在上是增函数.

设，

则，

当时，，，，，

则，在上递减.

不妨设，由于在上是增函数，则，

又，，则，于是，

由，在上递减，

则，所以，

则，

又，，在上是增函数，

所以，，即.

（二）选考题：（任选一题作答，共10分）

22.（Ⅰ）由平方取和有，

则曲线的普通方程为；代入，有曲线的极坐标方程.

（Ⅱ）由射线：与曲线交于点，有，

又射线：与直线交于点，所以代入得，

因为、、三点共线，所以。

23.（Ⅰ）因为即，，

解得，所以不等式的解集为.

（Ⅱ）由，易知，即。

由柯西不等式知，即由，有，即不可能有，

所以不存在正数，，同时满足：，.