2021届中考数学专题专练之函数（一）一次函数A卷

这是一份2021届中考数学专题专练之函数（一）一次函数A卷，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1.点在一次函数的图象上，则m等于( )
A.B.5C.D.1
2.直线上有三个点，则的大小关系是( )
A.B.C.D.
3.将直线向上平移两个单位，平移后的直线所对应的函数关系式为( )
A.B.C.D.
4.如图，直线与y轴交于点，与x轴交于点，当a满足时，k的取值范围是( )
A.B.C.D.
5.如图，直线过点，则方程的解是( )
A.B.C.D.
6.对于实数，我们定义符号：当时，；当时，.例如，.若关于的函数为，则该函数的最小值是( )
A.0B.2C.3D.4
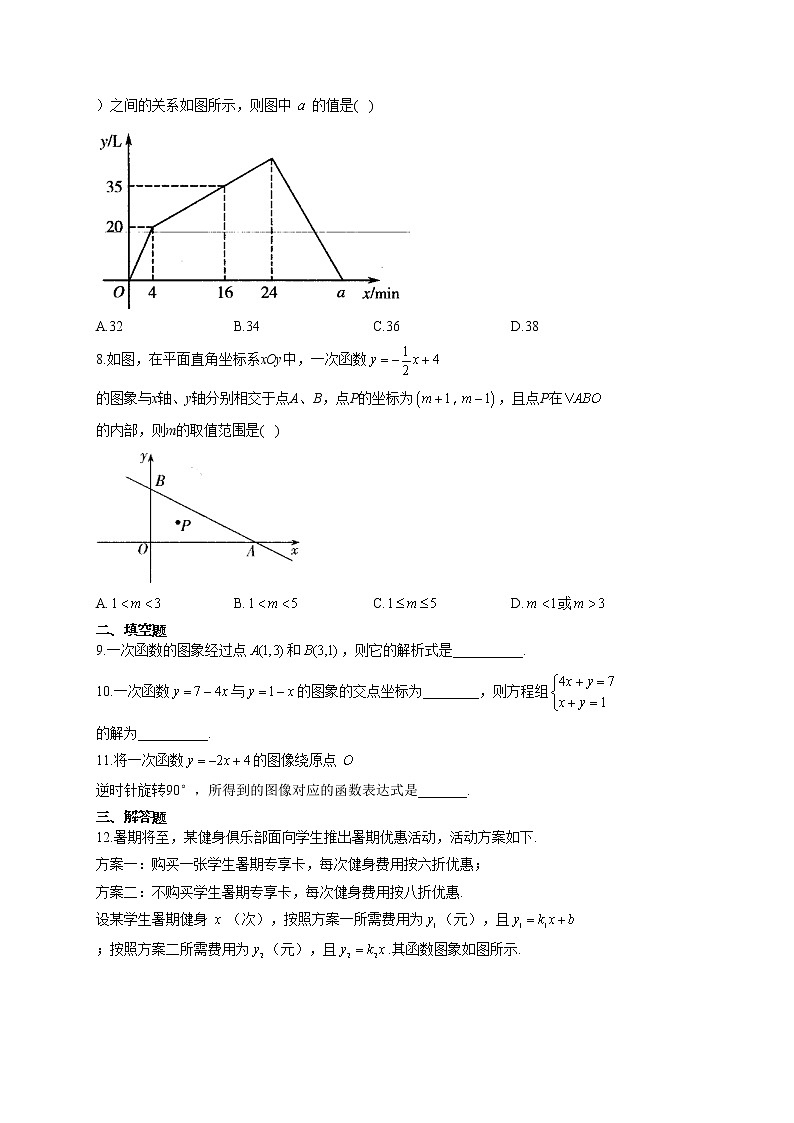
7.一个容器有进水管和出水管，每分钟的进水量和出水量是两个常数.从某时刻开始内只进水不出水，从第到第内既进水又出水，从第开始只出水不进水，容器内水量（单位：）与时间（单位：）之间的关系如图所示，则图中的值是( )
A.32B.34C.36D.38
8.如图，在平面直角坐标系xOy中，一次函数的图象与x轴、y轴分别相交于点A、B，点P的坐标为，且点P在的内部，则m的取值范围是( )
A.B.C.D.或
二、填空题
9.一次函数的图象经过点和，则它的解析式是__________.
10.一次函数与的图象的交点坐标为________，则方程组的解为__________.
11.将一次函数的图像绕原点逆时针旋转90°，所得到的图像对应的函数表达式是_______.
三、解答题
12.暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下.
方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；
方案二：不购买学生暑期专享卡，每次健身费用按八折优惠.
设某学生暑期健身（次），按照方案一所需费用为（元），且；按照方案二所需费用为（元），且.其函数图象如图所示.
（1）求和的值，并说明它们的实际意义；
（2）求打折前的每次健身费用和的值；
（3）八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少？说明理由.
参考答案
1.答案：D
解析：一次函数的图象经过点，解得，故选D.
2.答案：A
解析：y随x的增大而减小.又，.故选A.
3.答案：C
解析：直线向上平移两个单位，所得的直线是，故选C.
4.答案：C
解析：把点代入，得.则，解得.故选C.
5.答案：A
解析：方程的解即为函数的图象与x轴交点的横坐标，直线过，方程的解是，故选A.
6.答案：B
解析：当，即时，，随的增大而增大，当时，取得最小值，；当，即时，.综上所述，，.故选B.
7.答案：C
解析：本题考查一次函数的实际应用.由图象可知，进水的速度为，出水的速度为，第24分钟时的水量为，所以，故选C.
8.答案：A
解析：在函数中，令得，令得，则，
点P在的内部，
.故选A.
9.答案：
解析：设直线AB的函数解析式为（k、b为常数且），
一次函数的图象经过点，
，解得，
直线AB的函数解析式为.
10.答案：；
解析：在同一直角坐标系中作出一次函数与的图象，如图所示，由图象可知两图象的交点坐标为.由，得.由，得，故方程组的解为.
11.答案：
解析：本题考查图形旋转的性质、一次函数的图像与性质.根据题意，令，则，即直线与轴的交点坐标为，令，则，即直线与轴的交点坐标为.将直线绕原点逆时针方向旋转90°后，所得直线与轴的交点坐标变为，与轴的交点坐标变为，设旋转后的直线解析式为，可得，解得，旋转后的图像所对应的函数表达式.
12.答案：（1）的图象过点和点，
的实际意义是：打六折后的每次健身费用为15元.
的实际意义是：每张学生暑期专享卡的价格为30元.
（2）打折前的每次健身费用为（元）.
.
（3）.
.
当时，.
解得.
结合函数图象可知，小华暑期前往该俱乐部健身8次，选择方案一所需费用更少.
解析：