2017年江苏省盐城市中考数学试卷(解析版)

这是一份2017年江苏省盐城市中考数学试卷(解析版)，共34页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2017年江苏省盐城市中考数学试卷
　
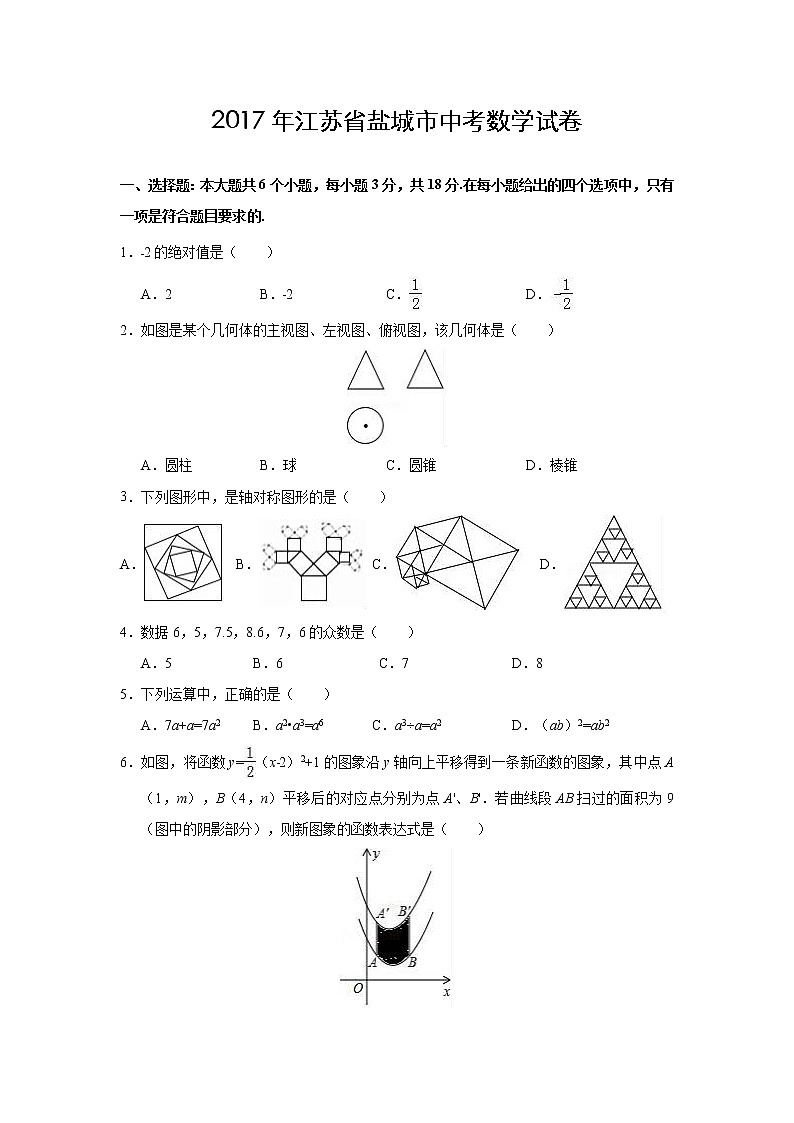
一、选择题：本大题共6个小题，每小题3分，共18分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．﹣2的绝对值是（　　）
A．2 B．﹣2 C． D．
2．如图是某个几何体的主视图、左视图、俯视图，该几何体是（　　）

A．圆柱 B．球 C．圆锥 D．棱锥
3．下列图形中，是轴对称图形的是（　　）
A． B． C． D．
4．数据6，5，7.5，8.6，7，6的众数是（　　）
A．5 B．6 C．7 D．8
5．下列运算中，正确的是（　　）
A．7a+a=7a2 B．a2•a3=a6 C．a3÷a=a2 D．（ab）2=ab2
6．如图，将函数y=（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（　　）

A．;B．;C． ;D．
　
二、填空题（每题3分，满分30分，将答案填在答题纸上）
7．请写出一个无理数　 　．
8．分解因式a2b﹣a的结果为　 　．
9．2016年12月30日，盐城市区内环高架快速路网二期工程全程全线通车，至此，已通车的内环高架快速路里程达57000米，用科学记数法表示数57000为　 　．
10．若在实数范围内有意义，则x的取值范围是　 　．
11．如图，是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是　 　．

12．在“三角尺拼角”实验中，小明同学把一副三角尺按如图所示的方式放置，则∠1=　 　°．

13．若方程x2﹣4x+1=0的两根是x1，x2，则x1（1+x2）+x2的值为　 　．
14．如图，将⊙O沿弦AB折叠，点C在上，点D在上，若∠ACB=70°，则∠ADB=　 　°．

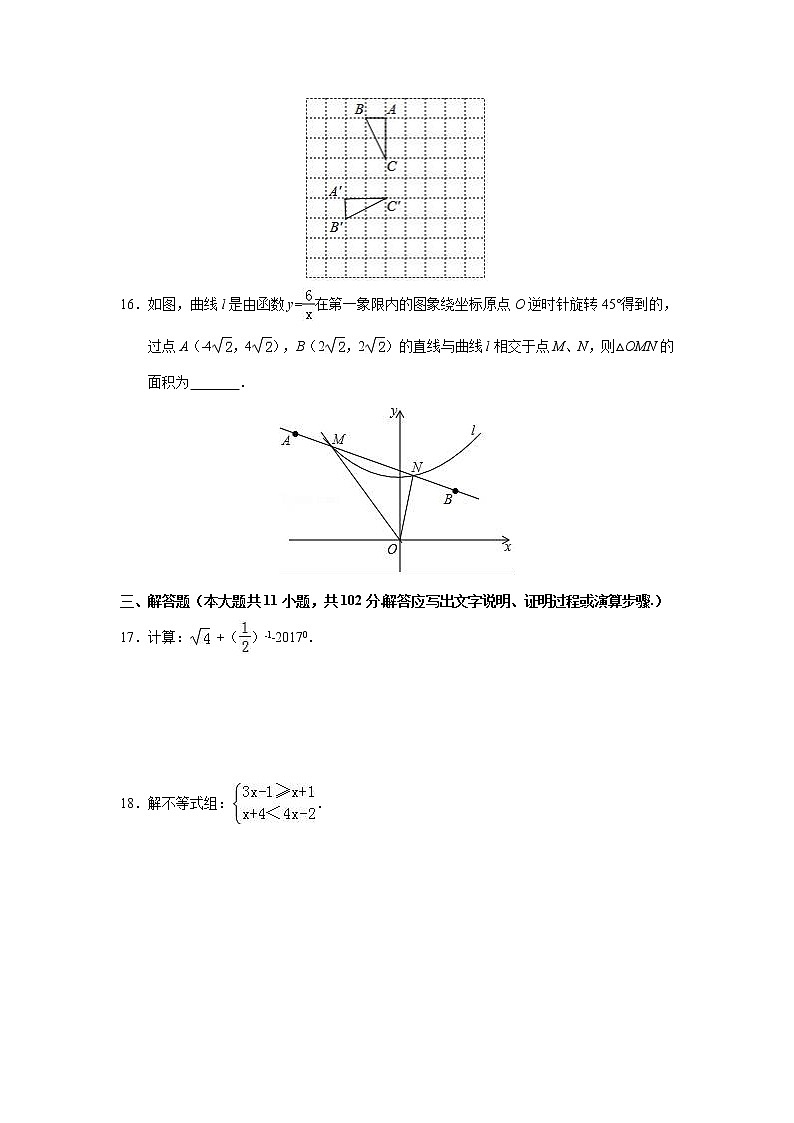
15．如图，在边长为1的小正方形网格中，将△ABC绕某点旋转到△A'B'C'的位置，则点B运动的最短路径长为　 　．

16．如图，曲线l是由函数y=在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（﹣4，4），B（2，2）的直线与曲线l相交于点M、N，则△OMN的面积为　 　．

三、解答题（本大题共11小题，共102分.解答应写出文字说明、证明过程或演算步骤.）
17．计算： +（）﹣1﹣20170．




18．解不等式组：．






19．先化简，再求值：÷（x+2﹣），其中x=3+．












20．为了编撰祖国的优秀传统文化，某校组织了一次“诗词大会”，小明和小丽同时参加，其中，有一道必答题是：从如图所示的九宫格中选取七个字组成一句唐诗，其答案为“山重水复疑无路”．
（1）小明回答该问题时，对第二个字是选“重”还是选“穷”难以抉择，若随机选择其中一个，则小明回答正确的概率是　 　；
（2）小丽回答该问题时，对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择，若分别随机选择，请用列表或画树状图的方法求小丽回答正确的概率．






21．“大美湿地，水韵盐城”．某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，下面是根据调查结果进行数据整理后绘制出的不完整的统计图：

请根据图中提供的信息，解答下列问题：
（1）求被调查的学生总人数；
（2）补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；
（3）若该校共有800名学生，请估计“最想去景点B“的学生人数．





22．如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．
（1）求证：四边形BEDF是平行四边形；
（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．






23．某商店在2014年至2016年期间销售一种礼盒．2014年，该商店用3500元购进了这种礼盒并且全部售完；2016年，这种礼盒的进价比2014年下降了11元/盒，该商店用2400元购进了与2014年相同数量的礼盒也全部售完，礼盒的售价均为60元/盒．
（1）2014年这种礼盒的进价是多少元/盒？
（2）若该商店每年销售这种礼盒所获利润的年增长率相同，问年增长率是多少？








24．如图，△ABC是一块直角三角板，且∠C=90°，∠A=30°，现将圆心为点O的圆形纸片放置在三角板内部．
（1）如图①，当圆形纸片与两直角边AC、BC都相切时，试用直尺与圆规作出射线CO；（不写作法与证明，保留作图痕迹）
（2）如图②，将圆形纸片沿着三角板的内部边缘滚动1周，回到起点位置时停止，若BC=9，圆形纸片的半径为2，求圆心O运动的路径长．





25．如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE平分∠BAC交边BC于点E，经过点A、D、E的圆的圆心F恰好在y轴上，⊙F与y轴相交于另一点G．
（1）求证：BC是⊙F的切线；
（2）若点A、D的坐标分别为A（0，﹣1），D（2，0），求⊙F的半径；
（3）试探究线段AG、AD、CD三者之间满足的等量关系，并证明你的结论．










26．【探索发现】
如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为　 　．

【拓展应用】
如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为　 　．（用含a，h的代数式表示）
【灵活应用】
如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．
【实际应用】
如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．
27．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．
（1）求抛物线的函数表达式；
（2）点D为直线AC上方抛物线上一动点；
①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；
②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．

　
2017年江苏省盐城市中考数学试卷
参考答案与试题解析
一、选择题：本大题共6个小题，每小题3分，共18分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．﹣2的绝对值是（　　）
A．2 B．﹣2 C． D．
【考点】15：绝对值．
【分析】根据负数的绝对值等于它的相反数解答．
【解答】解：﹣2的绝对值是2，
即|﹣2|=2．
故选：A．

2．如图是某个几何体的主视图、左视图、俯视图，该几何体是（　　）

A．圆柱 B．球 C．圆锥 D．棱锥
【考点】U3：由三视图判断几何体．
【分析】根据三视图即可判断该几何体．
【解答】解：由于主视图与左视图是三角形，
俯视图是圆，故该几何体是圆锥，
故选（C）
　
3．下列图形中，是轴对称图形的是（　　）
A． B． C． D．
【考点】P3：轴对称图形．
【分析】根据轴对称图形的概念求解．
【解答】解：D的图形沿中间线折叠，直线两旁的部分可重合，
故选：D．
　
4．数据6，5，7.5，8.6，7，6的众数是（　　）
A．5 B．6 C．7 D．8
【考点】W5：众数．
【分析】直接利用众数的定义分析得出答案．
【解答】解：∵数据6，5，7.5，8.6，7，6中，6出现次数最多，
故6是这组数据的众数．
故选：B．
　
5．下列运算中，正确的是（　　）
A．7a+a=7a2 B．a2•a3=a6 C．a3÷a=a2 D．（ab）2=ab2
【考点】47：幂的乘方与积的乘方；35：合并同类项；46：同底数幂的乘法．
【分析】根据合并同类项法则、同底数幂的乘法、除法法则、积的乘方法则一一计算即可判断．
【解答】解：
A、错误、7a+a=8a．
B、错误．a2•a3=a5．
C、正确．a3÷a=a2．
D、错误．（ab）2=a2b2
故选C．
　
6．如图，将函数y=（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（　　）

A． B． C． D．
【考点】H6：二次函数图象与几何变换．
【分析】先根据二次函数图象上点的坐标特征求出A、B两点的坐标，再过A作AC∥x轴，交B′B的延长线于点C，则C（4，1），AC=4﹣1=3，根据平移的性质以及曲线段AB扫过的面积为9（图中的阴影部分），得出AA′=3，然后根据平移规律即可求解．
【解答】
解：∵函数y=（x﹣2）2+1的图象过点A（1，m），B（4，n），
∴m=（1﹣2）2+1=1，n=（4﹣2）2+1=3，
∴A（1，1），B（4，3），
过A作AC∥x轴，交B′B的延长线于点C，则C（4，1），
∴AC=4﹣1=3，
∵曲线段AB扫过的面积为9（图中的阴影部分），
∴AC•AA′=3AA′=9，
∴AA′=3，
即将函数y=（x﹣2）2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象，
∴新图象的函数表达式是y=（x﹣2）2+4．
故选D．
　
二、填空题（每题3分，满分30分，将答案填在答题纸上）
7．请写出一个无理数　　．
【考点】26：无理数．
【分析】根据无理数定义，随便找出一个无理数即可．
【解答】解：是无理数．
故答案为：．
　
8．分解因式a2b﹣a的结果为　a（ab﹣1）　．
【考点】55：提公因式法与公式法的综合运用．
【分析】根据提公因式法分解即可．
【解答】解：a2b﹣a=a（ab﹣1），
故答案为：a（ab﹣1）．
　
9．2016年12月30日，盐城市区内环高架快速路网二期工程全程全线通车，至此，已通车的内环高架快速路里程达57000米，用科学记数法表示数57000为　5.7×104　．
【考点】1I：科学记数法—表示较大的数．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：将57000用科学记数法表示为：5.7×104．
故答案为：5.7×104．
　
10．若在实数范围内有意义，则x的取值范围是　x≥3　．
【考点】72：二次根式有意义的条件．
【分析】根据被开方数大于等于0列式进行计算即可求解．
【解答】解：根据题意得x﹣3≥0，
解得x≥3．
故答案为：x≥3．
　
11．如图，是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是　　．

【考点】X4：概率公式．
【分析】共有3种情况，上方的正六边形涂红色的情况只有1种，利用概率公式可得答案．
【解答】解：上方的正六边形涂红色的概率是，
故答案为：．
　
12．在“三角尺拼角”实验中，小明同学把一副三角尺按如图所示的方式放置，则∠1=　120　°．

【考点】K8：三角形的外角性质；K7：三角形内角和定理．
【分析】根据三角形的外角的性质计算即可．
【解答】解：由三角形的外角的性质可知，∠1=90°+30°=120°，
故答案为：120．
　
13．若方程x2﹣4x+1=0的两根是x1，x2，则x1（1+x2）+x2的值为　5　．
【考点】AB：根与系数的关系．
【分析】先根据根与系数的关系得到x1+x2=4，x1x2=1，然后把x1（1+x2）+x2展开得到x1+x2+x1x2，然后利用整体代入的方法计算即可．
【解答】解：根据题意得x1+x2=4，x1x2=1，
所以x1（1+x2）+x2=x1+x1x2+x2
=x1+x2+x1x2
=4+1
=5．
故答案为5．
　
14．如图，将⊙O沿弦AB折叠，点C在上，点D在上，若∠ACB=70°，则∠ADB=　110　°．

【考点】M5：圆周角定理．
【分析】根据圆周角定理和圆内接四边形的性质即可得到结论．
【解答】解：∵点C在上，点D在上，若∠ACB=70°，
∴∠ADB+∠ACB=180°，
∴∠ADB=110°，
故答案为：110．
　
15．如图，在边长为1的小正方形网格中，将△ABC绕某点旋转到△A'B'C'的位置，则点B运动的最短路径长为　π　．

【考点】O4：轨迹；R2：旋转的性质．
【分析】如图作线段AA′、CC′的垂直平分线相交于点P，点P即为旋转中心，观察图象可知，旋转角为90°（逆时针旋转）时B运动的路径长最短
【解答】解：如图作线段AA′、CC′的垂直平分线相交于点P，点P即为旋转中心，
观察图象可知，旋转角为90°（逆时针旋转）时B运动的路径长最短，PB==，
∴B运动的最短路径长为==π，
故答案为π．

　
16．如图，曲线l是由函数y=在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（﹣4，4），B（2，2）的直线与曲线l相交于点M、N，则△OMN的面积为　8　．

【考点】R7：坐标与图形变化﹣旋转；G5：反比例函数系数k的几何意义．
【分析】由题意A（﹣4，4），B（2，2），可知OA⊥OB，建立如图新的坐标系（OB为x′轴，OA为y′轴，利用方程组求出M、N的坐标，根据S△OMN=S△OBM﹣S△OBN计算即可．
【解答】解：∵A（﹣4，4），B（2，2），
∴OA⊥OB，
建立如图新的坐标系（OB为x′轴，OA为y′轴．

在新的坐标系中，A（0，8），B（4，0），
∴直线AB解析式为y′=﹣2x′+8，
由，解得或，
∴M（1.6），N（3，2），
∴S△OMN=S△OBM﹣S△OBN=•4•6﹣•4•2=8，
故答案为8
　
三、解答题（本大题共11小题，共102分.解答应写出文字说明、证明过程或演算步骤.）
17．计算： +（）﹣1﹣20170．
【考点】2C：实数的运算；6E：零指数幂；6F：负整数指数幂．
【分析】首先计算开方，乘方、然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可．
【解答】解：原式=2+2﹣1=3．
　
18．解不等式组：．
【考点】CB：解一元一次不等式组．
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
【解答】解：解不等式3x﹣1≥x+1，得：x≥1，
解不等式x+4＜4x﹣2，得：x＞2，
∴不等式组的解集为x＞2．
　
19．先化简，再求值：÷（x+2﹣），其中x=3+．
【考点】6D：分式的化简求值．
【分析】原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把x的值代入计算即可求出值．
【解答】解：原式=÷（﹣）
=÷
=•
=，
当x=3+时，原式===．
　
20．为了编撰祖国的优秀传统文化，某校组织了一次“诗词大会”，小明和小丽同时参加，其中，有一道必答题是：从如图所示的九宫格中选取七个字组成一句唐诗，其答案为“山重水复疑无路”．
（1）小明回答该问题时，对第二个字是选“重”还是选“穷”难以抉择，若随机选择其中一个，则小明回答正确的概率是　　；
（2）小丽回答该问题时，对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择，若分别随机选择，请用列表或画树状图的方法求小丽回答正确的概率．

【考点】X6：列表法与树状图法；X4：概率公式．
【分析】（1）利用概率公式直接计算即可；
（2）画出树状图得到所有可能的结果，再找到回答正确的数目即可求出小丽回答正确的概率．
【解答】解：
（1）∵对第二个字是选“重”还是选“穷”难以抉择，
∴若随机选择其中一个正确的概率=，
故答案为：；
（2）画树形图得：

由树状图可知共有4种可能结果，其中正确的有1种，
所以小丽回答正确的概率=．
　
21．“大美湿地，水韵盐城”．某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，下面是根据调查结果进行数据整理后绘制出的不完整的统计图：

请根据图中提供的信息，解答下列问题：
（1）求被调查的学生总人数；
（2）补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；
（3）若该校共有800名学生，请估计“最想去景点B“的学生人数．
【考点】VC：条形统计图；V5：用样本估计总体；VB：扇形统计图．
【分析】（1）用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数；
（2）先计算出最想去D景点的人数，再补全条形统计图，然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数；
（3）用800乘以样本中最想去A景点的人数所占的百分比即可．
【解答】解：（1）被调查的学生总人数为8÷20%=40（人）；
（2）最想去D景点的人数为40﹣8﹣14﹣4﹣6=8（人），
补全条形统计图为：

扇形统计图中表示“最想去景点D”的扇形圆心角的度数为×360°=72°；
（3）800×=280，
所以估计“最想去景点B“的学生人数为280人．
　
22．如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．
（1）求证：四边形BEDF是平行四边形；
（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．

【考点】LB：矩形的性质；L7：平行四边形的判定与性质；L9：菱形的判定．
【分析】（1）由矩形可得∠ABD=∠CDB，结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB，即可知BE∥DF，根据AD∥BC即可得证；
（2）当∠ABE=30°时，四边形BEDF是菱形，由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°，结合∠A=90°可得∠EDB=∠EBD=30°，即EB=ED，即可得证．
【解答】证明：（1）∵四边形ABCD是矩形，
∴AB∥DC、AD∥BC，
∴∠ABD=∠CDB，
∵BE平分∠ABD、DF平分∠BDC，
∴∠EBD=∠ABD，∠FDB=∠BDC，
∴∠EBD=∠FDB，
∴BE∥DF，
又∵AD∥BC，
∴四边形BEDF是平行四边形；

（2）当∠ABE=30°时，四边形BEDF是菱形，
∵BE平分∠ABD，
∴∠ABD=2∠ABE=60°，∠EBD=∠ABE=30°，
∵四边形ABCD是矩形，
∴∠A=90°，
∴∠EDB=90°﹣∠ABD=30°，
∴∠EDB=∠EBD=30°，
∴EB=ED，
又∵四边形BEDF是平行四边形，
∴四边形BEDF是菱形．
　
23．某商店在2014年至2016年期间销售一种礼盒．2014年，该商店用3500元购进了这种礼盒并且全部售完；2016年，这种礼盒的进价比2014年下降了11元/盒，该商店用2400元购进了与2014年相同数量的礼盒也全部售完，礼盒的售价均为60元/盒．
（1）2014年这种礼盒的进价是多少元/盒？
（2）若该商店每年销售这种礼盒所获利润的年增长率相同，问年增长率是多少？
【考点】AD：一元二次方程的应用；B7：分式方程的应用．
【分析】（1）设2014年这种礼盒的进价为x元/盒，则2016年这种礼盒的进价为（x﹣11）元/盒，根据2014年花3500元与2016年花2400元购进的礼盒数量相同，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）设年增长率为m，根据数量=总价÷单价求出2014年的购进数量，再根据2014年的销售利润×（1+增长率）2=2016年的销售利润，即可得出关于m的一元二次方程，解之即可得出结论．
【解答】解：（1）设2014年这种礼盒的进价为x元/盒，则2016年这种礼盒的进价为（x﹣11）元/盒，
根据题意得： =，
解得：x=35，
经检验，x=35是原方程的解．
答：2014年这种礼盒的进价是35元/盒．
（2）设年增长率为m，
2014年的销售数量为3500÷35=100（盒）．
根据题意得：（60﹣35）×100（1+a）2=（60﹣35+11）×100，
解得：a=0.2=20%或a=﹣2.2（不合题意，舍去）．
答：年增长率为20%．
　
24．如图，△ABC是一块直角三角板，且∠C=90°，∠A=30°，现将圆心为点O的圆形纸片放置在三角板内部．
（1）如图①，当圆形纸片与两直角边AC、BC都相切时，试用直尺与圆规作出射线CO；（不写作法与证明，保留作图痕迹）
（2）如图②，将圆形纸片沿着三角板的内部边缘滚动1周，回到起点位置时停止，若BC=9，圆形纸片的半径为2，求圆心O运动的路径长．

【考点】O4：轨迹；MC：切线的性质；N3：作图—复杂作图．
【分析】（1）作∠ACB的平分线得出圆的一条弦，再作此弦的中垂线可得圆心O，作射线CO即可；
（2）添加如图所示辅助线，圆心O的运动路径长为，先求出△ABC的三边长度，得出其周长，证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形，得出∠OO1O2=60°=∠ABC、∠O1OO2=90°，从而知△OO1O2∽△CBA，利用相似三角形的性质即可得出答案．
【解答】解：（1）如图①所示，射线OC即为所求；


（2）如图，圆心O的运动路径长为，

过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB，垂足分别为点D、F、G，
过点O作OE⊥BC，垂足为点E，连接O2B，
过点O2作O2H⊥AB，O2I⊥AC，垂足分别为点H、I，
在Rt△ABC中，∠ACB=90°、∠A=30°，
∴AC===9，AB=2BC=18，∠ABC=60°，
∴C△ABC=9+9+18=27+9，
∵O1D⊥BC、O1G⊥AB，
∴D、G为切点，
∴BD=BG，
在Rt△O1BD和Rt△O1BG中，
∵，
∴△O1BD≌△O1BG（HL），
∴∠O1BG=∠O1BD=30°，
在Rt△O1BD中，∠O1DB=90°，∠O1BD=30°，
∴BD===2，
∴OO1=9﹣2﹣2=7﹣2，
∵O1D=OE=2，O1D⊥BC，OE⊥BC，
∴O1D∥OE，且O1D=OE，
∴四边形OEDO1为平行四边形，
∵∠OED=90°，
∴四边形OEDO1为矩形，
同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形，
又OE=OF，
∴四边形OECF为正方形，
∵∠O1GH=∠CDO1=90°，∠ABC=60°，
∴∠GO1D=120°，
又∵∠FO1D=∠O2O1G=90°，
∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC，
同理，∠O1OO2=90°，
∴△OO1O2∽△CBA，
∴=，即=，
∴=15+，即圆心O运动的路径长为15+．
　
25．如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE平分∠BAC交边BC于点E，经过点A、D、E的圆的圆心F恰好在y轴上，⊙F与y轴相交于另一点G．
（1）求证：BC是⊙F的切线；
（2）若点A、D的坐标分别为A（0，﹣1），D（2，0），求⊙F的半径；
（3）试探究线段AG、AD、CD三者之间满足的等量关系，并证明你的结论．

【考点】MR：圆的综合题．
【分析】（1）连接EF，根据角平分线的定义、等腰三角形的性质得到∠FEA=∠EAC，得到FE∥AC，根据平行线的性质得到∠FEB=∠C=90°，证明结论；
（2）连接FD，设⊙F的半径为r，根据勾股定理列出方程，解方程即可；
（3）作FR⊥AD于R，得到四边形RCEF是矩形，得到EF=RC=RD+CD，根据垂径定理解答即可．
【解答】（1）证明：连接EF，
∵AE平分∠BAC，
∴∠FAE=∠CAE，
∵FA=FE，
∴∠FAE=∠FEA，
∴∠FEA=∠EAC，
∴FE∥AC，
∴∠FEB=∠C=90°，即BC是⊙F的切线；

（2）解：连接FD，
设⊙F的半径为r，
则r2=（r﹣1）2+22，
解得，r=，即⊙F的半径为；

（3）解：AG=AD+2CD．
证明：作FR⊥AD于R，
则∠FRC=90°，又∠FEC=∠C=90°，
∴四边形RCEF是矩形，
∴EF=RC=RD+CD，
∵FR⊥AD，
∴AR=RD，
∴EF=RD+CD=AD+CD，
∴AG=2FE=AD+2CD．

　
26．【探索发现】
如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为　　．

【拓展应用】
如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为　　．（用含a，h的代数式表示）
【灵活应用】
如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．
【实际应用】
如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．
【考点】LO：四边形综合题．
【分析】【探索发现】：由中位线知EF=BC、ED=AB、由=可得；
【拓展应用】：由△APN∽△ABC知=，可得PN=a﹣PQ，设PQ=x，由S矩形PQMN=PQ•PN═﹣（x﹣）2+，据此可得；
【灵活应用】：添加如图1辅助线，取BF中点I，FG的中点K，由矩形性质知AE=EH20、CD=DH=16，分别证△AEF≌△HED、△CDG≌△HDE得AF=DH=16、CG=HE=20，从而判断出中位线IK的两端点在线段AB和DE上，利用【探索发现】结论解答即可；
【实际应用】：延长BA、CD交于点E，过点E作EH⊥BC于点H，由tanB=tanC知EB=EC、BH=CH=54，EH=BH=72，继而求得BE=CE=90，可判断中位线PQ的两端点在线段AB、CD上，利用【拓展应用】结论解答可得．
【解答】解：【探索发现】
∵EF、ED为△ABC中位线，
∴ED∥AB，EF∥BC，EF=BC，ED=AB，
又∠B=90°，
∴四边形FEDB是矩形，
则===，
故答案为：；

【拓展应用】
∵PN∥BC，
∴△APN∽△ABC，
∴=，即=，
∴PN=a﹣PQ，
设PQ=x，
则S矩形PQMN=PQ•PN=x（a﹣x）=﹣x2+ax=﹣（x﹣）2+，
∴当PQ=时，S矩形PQMN最大值为，
故答案为：；

【灵活应用】
如图1，延长BA、DE交于点F，延长BC、ED交于点G，延长AE、CD交于点H，取BF中点I，FG的中点K，

由题意知四边形ABCH是矩形，
∵AB=32，BC=40，AE=20，CD=16，
∴EH=20、DH=16，
∴AE=EH、CD=DH，
在△AEF和△HED中，
∵，
∴△AEF≌△HED（ASA），
∴AF=DH=16，
同理△CDG≌△HDE，
∴CG=HE=20，
∴BI==24，
∵BI=24＜32，
∴中位线IK的两端点在线段AB和DE上，
过点K作KL⊥BC于点L，
由【探索发现】知矩形的最大面积为×BG•BF=×（40+20）×（32+16）=720，
答：该矩形的面积为720；

【实际应用】

如图2，延长BA、CD交于点E，过点E作EH⊥BC于点H，
∵tanB=tanC=，
∴∠B=∠C，
∴EB=EC，
∵BC=108cm，且EH⊥BC，
∴BH=CH=BC=54cm，
∵tanB==，
∴EH=BH=×54=72cm，
在Rt△BHE中，BE==90cm，
∵AB=50cm，
∴AE=40cm，
∴BE的中点Q在线段AB上，
∵CD=60cm，
∴ED=30cm，
∴CE的中点P在线段CD上，
∴中位线PQ的两端点在线段AB、CD上，
由【拓展应用】知，矩形PQMN的最大面积为BC•EH=1944cm2，
答：该矩形的面积为1944cm2．
　
27．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．
（1）求抛物线的函数表达式；
（2）点D为直线AC上方抛物线上一动点；
①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；
②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．

【考点】HF：二次函数综合题．
【分析】（1）根据题意得到A（﹣4，0），C（0，2）代入y=﹣x2+bx+c，于是得到结论；
（2）①如图，令y=0，解方程得到x1=﹣4，x2=1，求得B（1，0），过D作DM⊥x轴于M，过B作BN⊥x轴交于AC于N，根据相似三角形的性质即可得到结论；
②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形，取AB的中点P，求得P（﹣，0），得到PA=PC=PB=，过作x轴的平行线交y轴于R，交AC的延线于G，情况一：如图，∠DCF=2∠BAC=∠DGC+∠CDG，情况二，∠FDC=2∠BAC，解直角三角形即可得到结论．
【解答】解：（1）根据题意得A（﹣4，0），C（0，2），
∵抛物线y=﹣x2+bx+c经过A、C两点，
∴，
∴，
∴y=﹣x2﹣x+2；
（2）①如图，令y=0，
∴﹣x2﹣x+2=0，
∴x1=﹣4，x2=1，
∴B（1，0），
过D作DM⊥x轴于M，过B作BN⊥x轴交于AC于N，
∴DM∥BN，
∴△DME∽△BNE，
∴==，
设D（a，=﹣a2﹣a+2），
∴M（a， a+2），
∵B（1.0），
∴N（1，），
∴==（a+2）2+；
∴当a=2时，的最大值是；
②∵A（﹣4，0），B（1，0），C（0，2），
∴AC=2，BC=，AB=5，
∴AC2+BC2=AB2，
∴△ABC是以∠ACB为直角的直角三角形，取AB的中点P，
∴P（﹣，0），
∴PA=PC=PB=，
∴∠CPO=2∠BAC，
∴tan∠CPO=tan（2∠BAC）=，
过作x轴的平行线交y轴于R，交AC的延长线于G，
情况一：如图，∴∠DCF=2∠BAC=∠DGC+∠CDG，
∴∠CDG=∠BAC，
∴tan∠CDG=tan∠BAC=，
即，
令D（a，﹣a2﹣a+2），
∴DR=﹣a，RC=﹣a2﹣a，
∴，
∴a1=0（舍去），a2=﹣2，
∴xD=﹣2，
情况二，∴∠FDC=2∠BAC，
∴tan∠FDC=，
设FC=4k，
∴DF=3k，DC=5k，
∵tan∠DGC==，
∴FG=6k，
∴CG=2k，DG=3k，∴
∴RC=k，RG=k，
DR=3k﹣k=k，
∴==，
∴a1=0（舍去），a2=，
点D的横坐标为﹣2或﹣．