人教版中考数学专题总复习《二次函数》练习题及答案精品教学课件PPT

这是一份人教版中考数学专题总复习《二次函数》练习题及答案精品教学课件PPT，共32页。PPT课件主要包含了解析选C，∴所求函数解析式为，∴AB5等内容，欢迎下载使用。

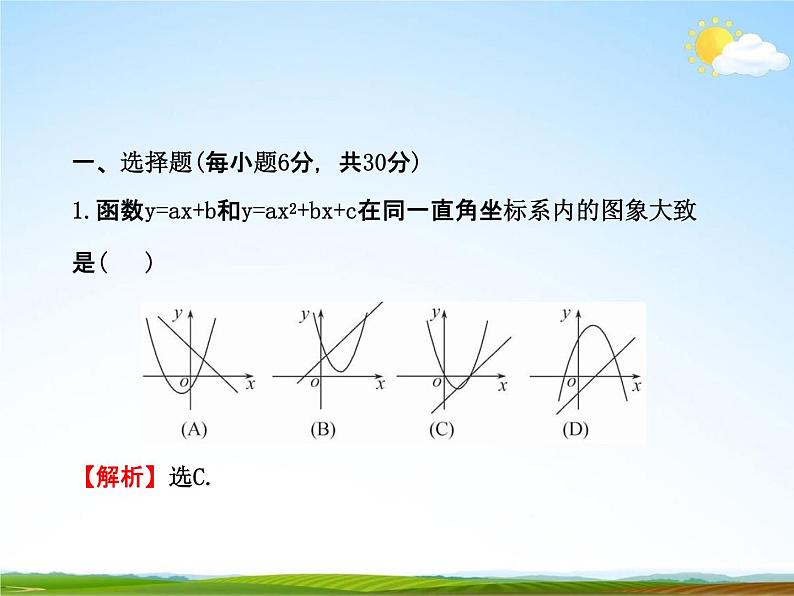
一、选择题(每小题6分，共30分)1.函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致 是()
2．把抛物线y=x2向右平移1个单位，所得抛物线的函数解析式为()(A)y=x2+1(B)y=(x+1)2(C)y=x2-1(D)y=(x-1)2【解析】选D.根据抛物线的平移规律，左右平移，变自变量， “左加右减”，故选D.
3.二次函数y=x2-x-2的图象如图所示，则函数值y＜0时x的取值范围是()(A)x＜-1(B)x＞2(C)-1＜x＜2(D)x＜-1或x＞2【解析】选C.由图象观察可得.
4.如图，两条抛物线y =-x +1、y =-x
-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成 的阴影部分的面积为()
(A)8(B)6(C)10(D)4【解析】选A.由图知y2可由y1向下平移2个单位得到，故阴影 部分的面积为2×4=8.
5.如图，点A，B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动，与x轴交于C、 D两点(C在D的左侧)，点C的横坐标最小值 为-3，则点D的横坐标最大值为( )(A)-3 (B)1 (C)5 (D)8【解析】选D.顶点在A处时点C的横坐标最小，此时D的横坐标 是5，当顶点在B处时，点D的横坐标最大.
二、填空题(每小题6分，共24分)6.若二次函数y=-x2+2x+k的部分图象如图所示，关于x的一元 二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=_____.
【解析】根据二次函数图象的对称性可得. 答案：-1
7．如图，抛物线y=ax2+bx+c与x轴的一个交点A在点(-2，0)和(-1，0)之间(包 括这两点)，顶点C是矩形DEFG上(包括边 界和内部)的一个动点，则 (1)abc______0(填“＞”或“＜”)； (2)a的取值范围是_____.【解析】(1)根据图象判断a,b,c的符号知abc<0; (2)根据顶点C的变化范围，求得答案：(1)＜(2)
8.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为_____.【解析】式子可变形为x+y=-x2-2x+3，利用配方法或公式法 可求得-x2-2x+3=-(x2+2x+1)+4=-(x+1)2+4.即：x+y的最大值为4. 答案：4
9.如图，小明的父亲在
相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距 地面高都是2.5米，绳子自然下垂呈抛物 线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距 离为_____米.【解析】建立直角坐标系，用待定系数法求出解析式，再根 据解析式求出最值.答案：12
三、解答题(共46分)10．(10分)用长为12 m的篱笆，一边利用 足够长的墙围出一块苗圃．如图，围出的 苗圃是五边形ABCDE，AE⊥AB，BC⊥AB，∠C=∠D=∠E．设CD=DE=x m，五边形ABCDE的面积为S m2．问 当x取什么值时，S最大?并求出S的最大值．
【解析】连结EC，作DF⊥EC，垂足为F.
∵∠DCB=∠CDE=∠DEA，∠EAB=∠CBA=90°，∴∠DCB=∠CDE=∠DEA=120°.∵DE=CD,∴∠DEC=∠DCE=30°，∴∠CEA=∠ECB=90°，∴四边形EABC为矩形，又∵DE=x，∴AE=6-x，DF= 1 x，EC= 3x，2
11.(12分)某市政府大力扶持大学生创业．李明在政府的扶持 下投资销售一种进价为每件20元的护眼台灯．销售过程中发 现，每月销售量y(件)与销售单价x(元)之间的关系可近似的 看作一次函数：y=-10x+500．设李明每月获得利润为w(元)，当销售单价定为多少元时， 每月可获得最大利润？如果李明想要每月获得2 000元的利润，那么销售单价应 定为多少元？根据物价部门规定，这种护眼台灯的销售单价不得高于32 元，如果李明想要每月获得的利润不低于2 000元，那么他每 月的成本最少需要多少元？(成本＝进价×销售量)
解析：(1)由题意，得：w=(x-20)·y
=(x-20)·(-10x+500)=-10x2+700x-10 000- b=35.
2a答：当销售单价定为35元时，每月可获得最大利润．(2)由题意，得：-10x2+700x-10 000=2 000解这个方程得：x1=30，x2=40．答：李明想要每月获得2 000元的利润，销售单价应定为30元 或40元.
(3)方法一：∵a=-10＜0，∴抛物线开口向下.∴当30≤x≤40时，w≥2 000．∵x≤32，∴当30≤x≤32时，w≥2 000． 设成本为P(元)，由题意，得： P=20×(-10x+500)=-200x+10 000∵k=-200＜0，∴P随x的增大而减小.∴当x=32时，P最小＝3 600.答：想要每月获得的利润不低于2 000元，每月的成本最少为 3 600元．
方法二：∵a=-10＜0,∴抛物线开口向下.∴当30≤x≤40时，w≥2 000.∵x≤32,∴30≤x≤32时，w≥2 000.∵y=-10x+500,k=-10＜0,∴y随x的增大而减小.∴当x=32时，y最小=180.∵当进价一定时，销售量越小，成本越小，∴20×180=3 600(元).答：想要每月获得的利润不低于2 000元，每月的成本最少为 3 600元．
12．(12分)如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B 两点的坐标分别为(-3，0)、(0，4)，抛物线y= 2 x2+bx+c经
过B点，且顶点在直线x=上．2
求抛物线对应的函数解析式；若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD 是菱形时，试判断点C和点D是否在该抛物线上，并说明理由； (3)若M点是CD所在直线下方该抛物线上的一个动点，过点M作 MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数解析式，并求l取最大值时，点M的坐 标．
【解析】(1)由题意，可设所求抛物线对应的函数解析式为
(2)在Rt△ABO中，OA=3，OB=4，
∴点C和点D在所求抛物线上．
∵四边形ABCD是菱形，∴BC=CD=DA=AB=5，∴C、D两点的坐标分别是(5，4)、(2，0)．当x=5时，y= 2×52- 10×5+4=4，
当x=2时，y= 2×22- 10×2+4=0，
(3)设直线CD对应的函数解析式为y=kx+b，
∵MN∥y轴，M点的横坐标为t，∴N点的横坐标也为t．
13．(12分)如图，已知抛物线C1：y=a(x+2)2－5的顶点为P， 与x轴相交于A、B两点(点A在点B的左边)，点B的横坐标是1． (1)求P点坐标及a的值；(2)如图(1)，抛物线C2与抛物线C1关 于x轴对称，将抛物线C2向右平移， 平移后的抛物线记为C3，C3的顶点为 M，当点P、M关于点B成中心对称时， 求C3的解析式；
(3)如图(2)，点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转 180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、 F两点(点E在点F的左边)，当以点P、N、F为顶点的三角形是 直角三角形时，求点Q的坐标．
【解析】(1)由抛物线C1：y=a(x+2)2－5得顶点P的坐标为 (-2，-5)，
∵点B(1，0)在抛物线C1上，
∴抛物线C 的解析式为y=－(x－4) +5.
∴0=a(1+2)2－5，解得，a＝ 9 .(2)如图(1)连结PM，作PH⊥x轴于H， 作MG⊥x轴于G，∵点P、M关于点B成中心对称，∴PM过点B，且PB＝MB，∴△PBH≌△MBG，∴MG＝PH＝5， BG＝BH＝3，∴顶点M的坐标为(4，5).抛物线C2由C1关于x轴对称得到，抛物线C3由C2平移得到，
(3)∵抛物线C4由C1绕点x轴上的点Q旋转180°得到，∴顶点N、P关于点Q成中心对称， 由(2)得点N的纵坐标为5.设点N坐标为(m，5),作PH⊥x轴于H，作NG⊥x轴于G, 作PK⊥NG于K.
∵旋转中心Q在x轴上，∴EF＝AB＝2BH＝6，∴FG＝3，点F坐标为(m+3，0)， H坐标为(-2，0)，K坐标为(m，-5)， 根据勾股定理得PN2＝NK2+PK2＝m2+4m+104， PF2＝PH2+HF2＝m2+10m+50， NF2＝52+32＝34.
①当∠PNF＝90°时，PN2+NF2＝PF2，
解得m＝ 44，∴Q点坐标为( 19 ，0);
②当∠PFN＝90°时，PF2+NF2＝PN2， 解得m＝ 10 ，∴Q点坐标为( 2 ，0);
3③∵PN＞NK＝10＞NF，∴∠NPF≠90°.
综上所得，当Q点坐标为( 19 ，0)或( 2，0)时，以点P、N、F
3为顶点的三角形是直角三角形．