人教版中考数学专题总复习《等腰三角形》练习题及答案精品教学课件PPT

这是一份人教版中考数学专题总复习《等腰三角形》练习题及答案精品教学课件PPT，共26页。PPT课件主要包含了即图3的一条腰长是，当⊙E与等内容，欢迎下载使用。

一、选择题(每小题6分，共30分)1.已知等腰三角形的一个内角为40°，则这个等腰三角形的 顶角为()(A)40°(B)100°(C)40°或100°(D)70°或50°【解析】选C.40°若是底角，则顶角为180°-40°×2=100°, 40°为顶角亦满足题意.
2.如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为 AC上一点，若∠APD=60°，则CD的长为()
【解析】选B.∵∠B=60°,∴∠BAP+∠APB=120°.∵∠APD=60°,∴∠CPD+∠APB=120°,∴∠BAP=∠DPC,∴△ABP∽△PCD,∵AB=3,BP=1,PC=2,∴CD= 2.3
3.如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是△ABC、△BCD的角平分线，则图中的等腰三角形有() (A)5个(B)4个(C)3个(D)2个
【解析】选A.因为AB=AC，∠A=36°，所以∠ABC=∠ACB=72°.由BD、CE分别是△ABC、△BCD的角平分线，可得∠ABD=∠CBD=∠ACE=∠BCE=36°,所以△ABC、△BCD、△ABD、△BCE、△DCE都为等腰三角形.
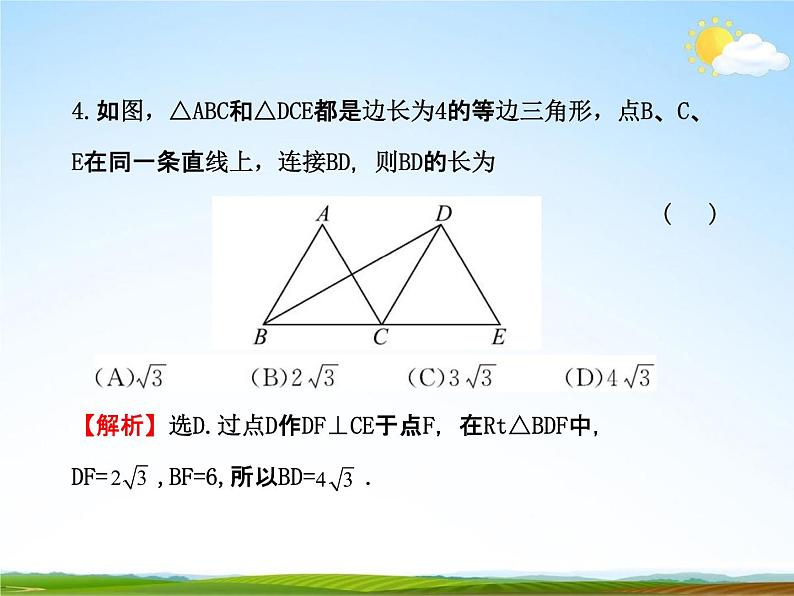
4.如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为()
【解析】选D.过点D作DF⊥CE于点F，在Rt△BDF中，DF= 23 ,BF=6,所以BD=43.
5.如图所示，已知等边三角形ABC的边长为1，按图中所示的 规律，用2 008个这样的三角形镶嵌而成的四边形的周长是()
(A)2 008 (B)2 009 (C)2 010 (D)2 011【解析】选C.第一个四边形由两个三角形组成，周长为4；第 二个四边形由三个三角形组成，周长为5；第三个四边形由四 个三角形组成，周长为6；…第n个四边形的周长为n+3，所以 由2 008个三角形组成的四边形的周长为2 010.
二、填空题(每小题6分，共24分)6.如图,在△ABC中,AD平分∠BAC,AB=AC-BD,则∠B∶∠C的值是_____.【解析】延长AB至E, 使AE=AC,连结DE,∵AD平分∠BAC,∴∠BAD=∠CAD.∵AD=AD,∴△AED≌△ACD,∴∠E=∠C.∵AB=AC-BD,∴AB=AE-BD=AB+BE-BD.∴BE=BD,∴∠E=∠BDE,∴∠ABC=∠E+∠BDE=2∠E=2∠C.即∠ABC∶∠C=2∶1. 答案：2∶1
7.在直角坐标系中，O为坐标原点，A(1，1)，在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有_____个.【解析】如图，以O为圆心，OA为半径作圆 交x轴于E、B，E、B可以为P；以A为圆心， AO为半径作圆交x轴于C,则C可以为P；作OA的中垂线交x轴于D.则D可以为P.所以符合条件的点P共4个. 答案：4
8.如图,在等边△ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE=_____度.【解析】∵△ABC为等边三角形，∴AB=AC=BC，∠A=∠ABC=∠ACB=60°.又∵AD=CE,∴△ACD≌△CBE,∴∠ACD=∠CBE,∴∠BCD+∠CBE=∠BCD+∠ACD=∠BCA=60°.答案：60
9.小敏将一张直角边为1的等腰直角三角形纸片(如图1)，沿 它的对称轴折叠1次后得到一个等腰直角三角形(如图2)，再 将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直 角三角形(如图3)，则图3中的等腰直角三角形的一条腰长为_____；同上操作，若小敏连续将图1的等腰直角三角形折叠n 次后所得到的等腰直角三角形(如图n+1)的一条腰长为_____.
【解析】第1次折叠，即图2的一条腰长是 2 ，第2次折叠，
22 )2，第3次折叠，即图4的一条腰长是
长是(2 )n.2答案
(2 )3，以此类推，第n次折叠后的等腰直角三角形的一条腰
三、解答题(共46分) 10.(10分)如图，在等边△ABC中，点D是BC边的中点，以 AD为边作等边△ADE.求∠CAE的度数；取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形.【解析】(1)在等边△ABC中，∵点D是BC的中点，∴∠DAC=30°，又∵△ADE是等边三角形，∴∠DAE=60°，∴∠CAE=∠DAE-∠DAC=30°.
(2)由(1)知，∠EAF=90°，由F为AB的中点知∠CFA=90°,∴CF∥EA，在等边△ABC中，CF=AD， 在等边△ADE中，AD=EA,∴CF=EA，∴四边形AFCE是平行四边形， 又∵∠CFA=90°，所以四边形AFCE是矩形.
11.(12分)如图，在△ABC中，BC>AC，点D在BC上，且DC＝ AC,∠ACB的平分线CF交AD于F，点E是AB的中点，连结EF. (1)求证：EF∥BC;
(2)若四边形BDFE的面积为6，求△ABD的面积.
【解析】(1)∵CF平分∠ACB,∴∠1=∠2. 又∵DC=AC,∴CF是△ACD的中线，∴点F是AD的中点.∵点E是AB的中点，∴EF∥BD,即EF∥BC.
(2)由(1)知，EF∥BD，
∴△AEF∽△ABD,∴
12.(12分)如图，在平行四边形ABCD中，BE平分∠ABC交AD于点E，DF平分∠ADC交BC于点F.
求证：△ABE≌△CDF;若BD⊥EF，则判断四边形EBFD是什么特殊四边形，请证明 你的结论.
【解析】(1)∵四边形ABCD是平行四边形，∴∠A=∠C，AB=CD，∠ABC=∠ADC.∵BE平分∠ABC，DF平分∠ADC，∴∠ABE=∠CDF,∴△ABE≌△CDF(ASA).(2)由△ABE≌△CDF,得AE=CF,在平行四边形ABCD中，AD∥BC，AD=BC,∴DE∥BF,DE=BF,∴四边形EBFD是平行四边形.若BD⊥EF，则四边形EBFD是菱形.
13．(12分)如图，等边三角形ABC边长为4，E是边BC上动点， EH⊥AC于H，过E作EF∥AC，交线段AB于点F，在线段AC上取点 P，使PE=EB.设EC=x(0＜x≤2).请直接写出图中与线段EF相等的两条 线段(不再另外添加辅助线)；Q是线段AC上的动点，当四边形EFPQ是平行四边形时,求EFPQ的面积(用含x的代数式表示)；当(2)中的EFPQ面积最大时，以E为圆心，r为半径作圆， 根据⊙E与此时EFPQ四条边交点的总个数，求相应的r的取 值范围.
【解析】(１)BE、PE、BF三条线段中任选两条．
(２)在Rt△CHE中，∠CHE＝90°，
∵PQ=EF=BE=4-x,
∠Ｃ＝60°，∴ＥH＝3 x.
∴当x＝２时，有最大值．此时E、F、P分别为△ABC三边BC、AB、AC的中点，且点C、点 Q重合.∴平行四边形EFPQ是菱形． 过Ｅ点作ＥD⊥ＦＰ于D，
四条边交点的总个数是２个时，
∴ＥD＝ＥH＝3 ．∴当⊙E与 ０＜r＜3 ；
四条边交点的总个数是４个时，
四条边交点的总个数是６个时，
四条边交点的总个数是３个时，
四条边交点的总个数是０个时，
r＝3 ； 当⊙E与3 ＜r＜２； 当⊙E与 r＝２；当⊙E与 r＞２．