人教版数学中考复习《二次函数的图象及性质》精品教学课件ppt优秀课件

这是一份人教版数学中考复习《二次函数的图象及性质》精品教学课件ppt优秀课件，共14页。PPT课件主要包含了列表参考等内容，欢迎下载使用。

二次函数y=ax2的图象和性质
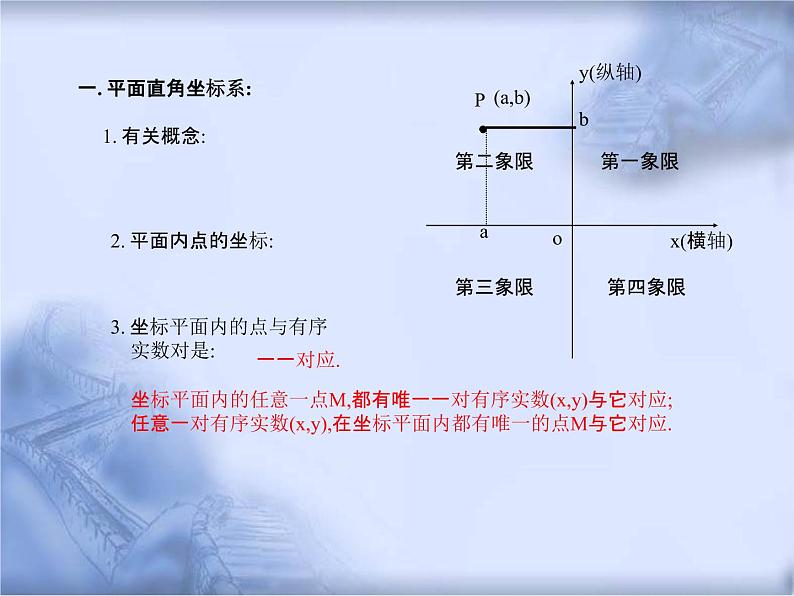
一. 平面直角坐标系:
2. 平面内点的坐标:
3. 坐标平面内的点与有序
坐标平面内的任意一点M,都有唯一一对有序实数(x,y)与它对应; 任意一对有序实数(x,y),在坐标平面内都有唯一的点M与它对应.
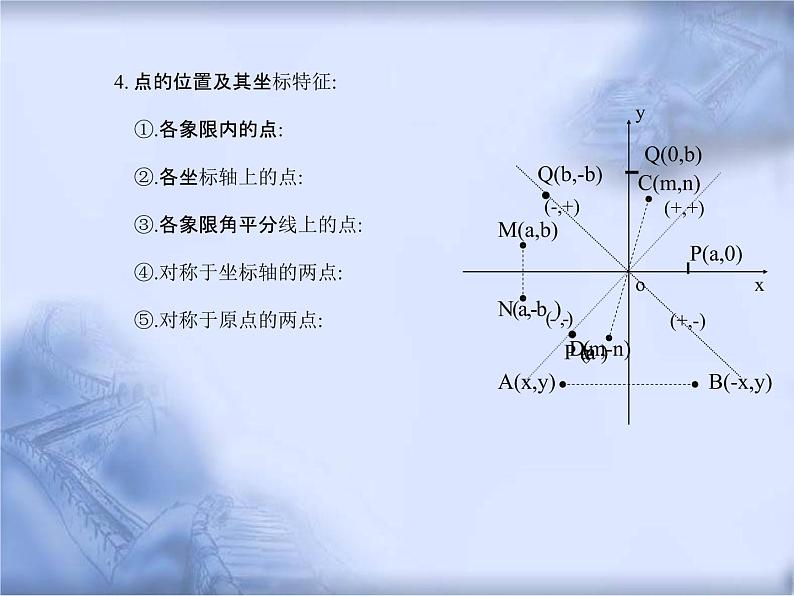
4. 点的位置及其坐标特征:
③.各象限角平分线上的点:
④.对称于坐标轴的两点:
⑤.对称于原点的两点:
Q(b,-b)(-,+)M(a,b)
Q(0,b)C(m,n)(+,+)
N(a,-b(-),-)PD(a(,-am) ,-n)A(x,y)
y   2y  1xx
用用光光滑滑曲曲线线连连结结时时要要
用光自自滑左左曲向向线右右连顺顺结次次时连连要结结
用用自用光用光左光滑光滑向滑曲滑曲右曲线曲线顺线连线连次连结连结连结时结时结时要时要要要
自自自左自左左向左向向右向右右顺右顺顺次顺次次连次连连结连结结结
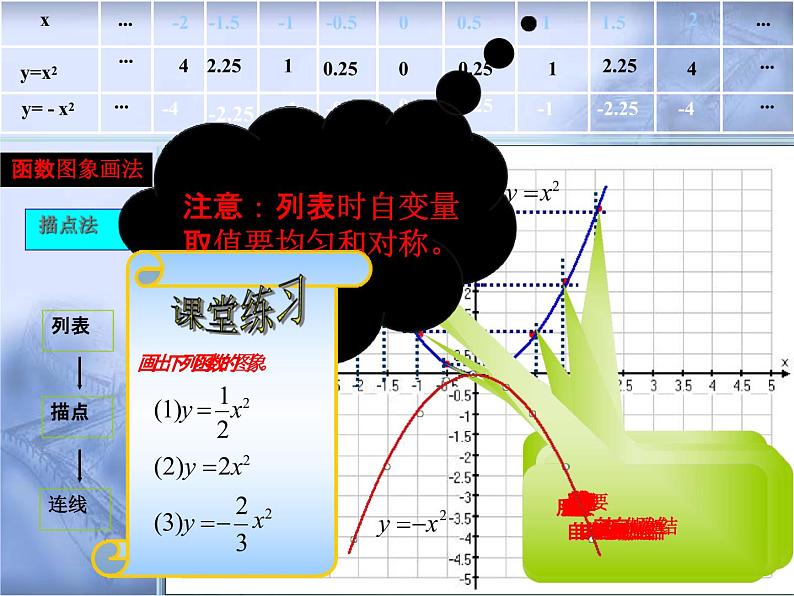
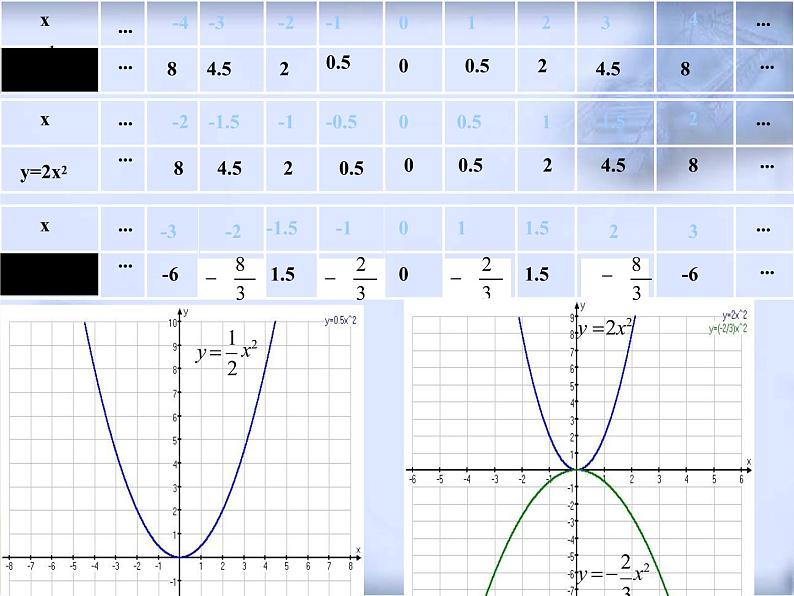
列表画出下列函数的图象。
(1)y  1 x2
283y  2x2
y   2 x23
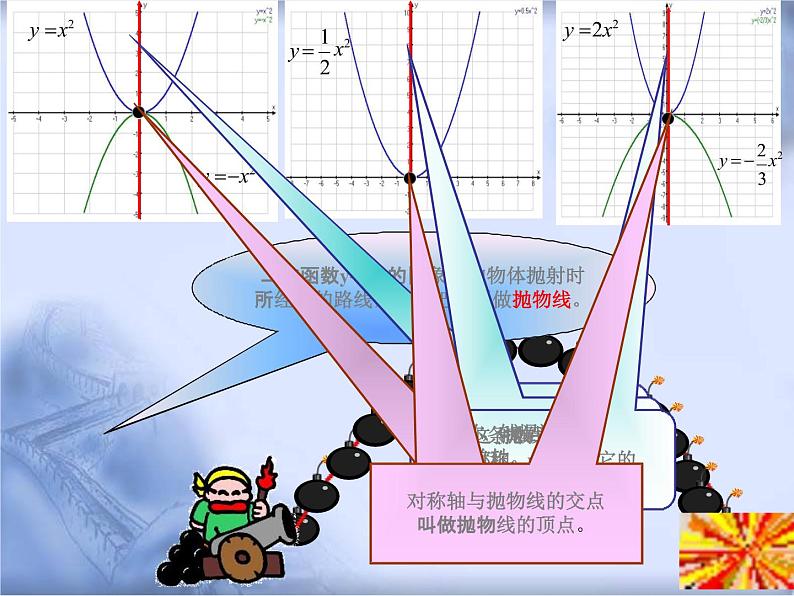
二次函数y=ax2的图象形如物体抛射时 所经过的路线，我们把它叫做抛物线。
对称这，条y抛轴物就线是关它于的y轴
对对称称轴，。y轴就是它的
对称轴与抛物线的交点 叫做抛物线的顶点。
在x轴的上方（除顶点外）
在x轴的下方（除顶点外）
当x=0时，最小值为0。
当x=0时，最大值为0。
二次函数y=ax2的性质 １、顶点坐标与对称轴
1、观察右图， 并完成填空。2、练习23、想一想4、练习4
在同在一同坐一标坐系标内系，内抛，物抛线物y线=xy2=与x2抛与物抛线物线
y= -x-x2y的2的轴位位置置有有什什么么关关系系？？如如果果在在同同一一坐坐标y标轴系系内内 画函画数函y数=ayx=2与axy2与= y-=ax2-的ax图2的象图，象怎，样怎画样才画简才便简？便？
答：抛物线抛物线y=x2与抛物线 y= -x2 既关于x轴对
称，又关于原点对称。只要画出y=ax 与y= -ax 中的
一条抛物线，另一条可利用关于x轴对称或关于原点
当a>0时，在对称轴的 左侧，y随着x的增大而减小。
当a>0时，在对称轴的 右侧，y随着x的增大而增大。
当a<0时，在对称轴的 左侧，y随着x的增大而增大。
2 当a<0时，在对称轴的
右侧，y随着x的增大而 减小。
当x=-2时，y=-4
当x=-1时，y=-1
1、抛物线y=ax2的顶点是原点，对称轴是y轴。
2、当a>0时，抛物线y=ax2在x轴的上方（除顶点外），它的开口向上，并且 向上无限伸展；当a<0时，抛物线y=ax2在x轴的下方（除顶点外），它的开口向下，并且 向下无限伸展。
3、当a>0时，在对称轴的左侧，y随着x的增大而减小；在对称轴右侧，y随着x的增大而增大。当x=0时函数y的值最小。 当a<0时，在对称轴的左侧，y随着x的增大而增大；在对称轴的右侧，y随着x增大而减小，当x=0时，函数y的值最大。
二次函数y=ax2的性质
2、根据左边已画好的函数图象填空：
左侧，y随着x的；在对称轴的右侧，y随着x的
，当x=0时，函数y的值最大，最大值是，
（1）抛物线y=2x2的顶点坐标是（0，0）, 对称轴是 y轴，在 对称轴的右侧， y随着x的增大而增大；在对称轴的左侧， y随着x的增大而减小，当x= 0时 ， 函数y的值最小，最小值是 0,抛物线y=2x2在x轴的 上方（除顶点外）。
（2）抛物线 y   2 x2在x轴的 下方（除顶点外），在对称轴的
当x 0时，y<0.
1、已知抛物线y=ax2经过点A（-2，-8）。求此抛物线的函数解析式；判断点B（-1，- 4）是否在此抛物线上。求出此抛物线上纵坐标为-6的点的坐标。
解（1）把（-2，-8）代入y=ax2,得-8=a(-2)2,解出a= -2,所求函数解析式为 y= -2x2.
，所以点B（-1 ，-4）
（2）因为  4  2(1)2不在此抛物线上。
（3）由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个，它们分别是(3,6)与(