吉林省吉林市普通中学2021届高三下学期第四次调研测试 数学（文）（含答案）

吉林市普通中学2020—2021学年度高中毕业班第四次调研测试

文科数学

本试卷共23小题，共150分，共6页，考试时间120分钟，考试结束后，将答题卡和试题卷一并交回.

注意事项：

1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条

形码、姓名、准考证号，并将条形码粘贴在答题卡的指定位置上.

2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案

的标号；非选择题答案必须使用0.5毫米黑色字迹的签字笔书写，字体工整、

笔迹清楚.

3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案

    无效.

4. 作图可先用铅笔画出，确定后必须用黑色字迹的签字笔描黑.

5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮

    纸刀.

第I卷（共60分）

一、选择题：本大题共12题，每小题5分，共60分. 在每小题给出的四个选项中，只有一个是符合题目要求.

1.  已知全集，，则集合=

A.                  B.

C.                D.  

2.  已知是第二象限角，则

A.          B.

C.         D.

3.  已知为虚数单位，若复数为纯虚数，则

A.                 B.

C. 或                        D.

4.  已知数列为等差数列，首项，公差，前项和，则

A.                             B.           

C.                            D.

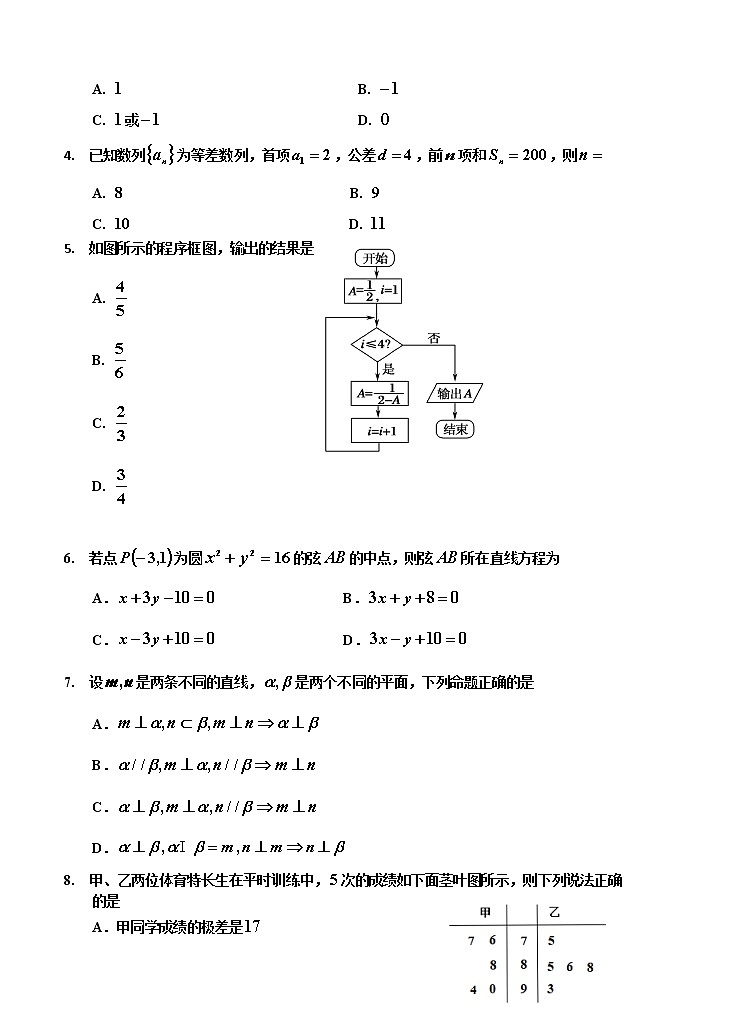
5.  如图所示的程序框图，输出的结果是

A.                   

B.

C.                 

D.

6.  若点为圆的弦的中点，则弦所在直线方程为

A．                  B．  

C．                  D．

7.  设是两条不同的直线，是两个不同的平面，下列命题正确的是

A．

B．

C．

D．

8.  甲、乙两位体育特长生在平时训练中，次的成绩如下面茎叶图所示，则下列说法正确

的是

A．甲同学成绩的极差是

B．乙同学的平均成绩较高

C．乙同学成绩的中位数是

D．甲同学成绩的方差较小

9.  已知,则的大小关系是

A.                       B.    

C.                        D.

10.  下列关于平面向量的说法正确的是

A．若共线，则点必在同一直线上

B．若且，则

C．若为的外心，则

D．若为的垂心，则

11.  已知函数在区间上单调递增，且在区间

上有且仅有一个解，则的取值范围是

1.    B.    C.            D.

12.  已知点是双曲线的右支上一点，为双曲线的左、右焦点，     的面积为，则下列说法正确的是

    ①点的横坐标为                    ②的周长为

③的内切圆半径为              ④的内切圆圆心横坐标为

A．②③④   B．①②④   C．①②③           D．①②

第II卷（共90分）

二、填空题：本大题共4个小题，每小题5分，共20分. 其中第16题的第一个空填对得2分，第二个空填对得3分.

13. 宋元时期是我国古代数学非常辉煌的时期，涌现了一大批卓有成就的数学家，其中秦九韶、李冶、杨辉和朱世杰成就最为突出，被誉为“宋元数学四大家”.现从秦九韶的《数书九章》、李冶的《测圆海镜》《益古演段》、杨辉的《详解九章算法》、朱世杰的《算学启蒙》《四元玉鉴》这六部著作中任选2本研读，则必选《数书九章》的概率是________．

14.  已知分别为三个内角的对边，且，

则         . 

15．已知函数，则     .

16．如图所示，在长方体中，

，点是棱

上的一个动点，若平面交棱于点

，则四棱锥的体积为       .

截面四边形的周长的最小值为      .

三、解答题：共70分. 解答应写出文字说明，证明过程或演算步骤. 第17～21题为必考题，每个试题考生都必须作答. 第22、23题为选考题，考生根据要求作答.

（一）必考题：共60分.

17.（本小题满分12分）

已知数列的前项和为，且满足.

（Ⅰ）求；

（Ⅱ）求.

18.（本小题满分12分）

如图，在三棱锥中，，，，，，为线段的中点，为线段上一点.

（Ⅰ）求证：；

（Ⅱ）求证：平面平面；
（Ⅲ）当平面时，求直线与

平面所成的角．

19.（本小题满分12分）

已知点是平面直角坐标系中异于原点的一个动点，过点且与轴垂直的直线与直线交于点，且向量与向量垂直.

（Ⅰ）求点的轨迹方程；

（Ⅱ）设位于第一象限，以为直径的圆与轴相交于点，且,求的值.

20.（本小题满分12分）

全球化时代，中国企业靠什么在激烈的竞争中成为世界一流企业呢？由人民日报社指导，《中国经济周刊》主办的第十八届中国经济论坛在人民日报社举行，就中国企业如何提升全球行业竞争力进行了研讨. 数据显示，某企业近年加大了科技研发资金的投入，其科技投入（百万元）与收益（百万元）的数据统计如下：

根据数据特点，甲认为样本点分布在指数型曲线的周围，据此他对数据进行了一些初步处理．如下表：

其中，．

（Ⅰ）请根据表中数据，建立关于的回归方程(系数精确到0.1)；

（Ⅱ）①乙认为样本点分布在直线的周围，并计算得回归方程为，

以及该回归模型的决定系数（即相关指数），试比较甲乙两人所建立的 模型，谁的拟合效果更好？

②由①所得的结论，计算该企业欲使收益达到1亿元，科技投入的费用至少要多少 百万元？（精确到0.1）

附：对于一组数据，，，，其回归直线方程的斜率和截距的最小二乘法估计分别为=，，决定系数：．

参考数据：.

21.（本小题满分12分）

已知函数.

（Ⅰ）当曲线在处的切线与直线垂直时，求实数的值；

（Ⅱ）求函数的单调区间.

（二）选考题：共10分.请考生在第22、23题中任选一题作答. 并用2B铅笔将所选题号涂黑，多涂、错涂、漏涂均不给分. 如果多做，则按所做的第一题计分.

22.  [选修4—4：坐标系与参数方程]

在平面直角坐标系中，点是曲线（为参数）上的动点，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（Ⅰ）求曲线的普通方程和曲线的直角坐标方程；

（Ⅱ）若点在轴右侧，点在曲线上，求的最小值.

23.  [选修4—5：不等式选讲]

设函数.

（Ⅰ）若，求证：；

（Ⅱ）对于，恒成立，求实数的取值范围.

吉林市普通中学2020—2021学年度高中毕业班第四次调研测试

文科数学参考答案

一、选择题：本大题共12题，每小题5分，共60分.

二、填空题：本大题共4个小题,每小题5分，共20分. 其中第16题的第一个空填对得2分，

第二个空填对得3分.

13.       14.        15.      16.   (2分)，  （3分）

17．【解析】

（Ⅰ）当时，                                     1分

                                       2分

                                       3分

                                          4分

（Ⅱ）当且时，                     6分

  即      ①                                    7分

由（Ⅰ）知       不符合式                                  8分

                                         10分

  因此                            12分

18.【解析】

(1)                        4分

(2) 

                                                                       8分

(3)    ，则为所求.

                      10分

(注：指出为所求，未证明扣1分）

又，

又，则

，则

即直线平面所成角为.                                          12分

19.【解析】

（1）设 ，则，

点的轨迹方程                                 5分

（注：也可以表示为（去除点），未去除点扣1分）

（2）由题知，，

所以直线倾斜角为，直线方程为，                 7分

由，解得   或

                                                       10分

                                       12分

（注：也可以设，代入求解）

20. 【解析】

（1）两边取对数得

令即   

根据最小二乘估计可知：，
得，
所以回归方程为，即                        5分

①甲建立的回归模型的．
所以甲建立的回归模型拟合效果更好．                          8分

（注：或均给分）
由①知，甲建立的回归模型拟合效果更好.设，解得

，   即．
所以科技投入的费用至少要百万元，下一年的收益才能达到亿．
21.【解析】

因为，

      所以                                      1分

根据题意                            2分

（1）解得 ，满足，                             4分

（2）

当时，，

令，令或

所以的递增区间是，递减区间是

当时，，

令，令

所以的递增区间是，递减区间是

综上所述：当时，的递增区间是，递减区间是；

当时，的递增区间是，递减区间是.                    12分

22.【解析】

（1）

消去得

即曲线的普通方程为                            2分

曲线的极坐标方程为 ，

由 得曲线的直角坐标方程为                   4分

（2）P是曲线右支上的动点  设点P坐标为

是曲线上   最小值即点P到曲线的距离          

则=                         7分

，，当且仅当时取等号

当时，取最小值 最小值为                        10分

23.【解析】

（Ⅰ）当时，                 2分

 当且仅当 等号成立  

                                                    4分

（注：没写取等号条件扣1分）

（Ⅱ）对于，恒成立

        恒成立     7分

     即   

实数的取值范围                              10分

法二：

（1）当时 即时，

                             6分

（2）当 即 时

①当时 ，

②当时 ，

由 ① ②可知                           9分

综上：的取值范围                            10分