湖南省娄底市新化县2021年中考模拟数学试卷

这是一份湖南省娄底市新化县2021年中考模拟数学试卷，共7页。试卷主要包含了一个数的绝对值是7，这个数是，下列计算正确的是等内容，欢迎下载使用。

一．选择题（共12小题，满分36分）
1．一个数的绝对值是7，这个数是（ ）
A．7B．﹣7C．7或﹣7D．不能确定
2．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．x2•x2＝2x4B．（﹣2a）3＝﹣6a3
C．（a3）2＝a6D．m3÷m3＝1
4．碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.5纳米的碳纳米管，1纳米＝0.000000001米，则0.5纳米用科学记数法表示为（ ）
A．0.5×10﹣9米B．5×10﹣8米C．5×10﹣9米D．5×10﹣10米
5．某同学参加射击训练，共发射8发子弹，击中的环数分别为5，3，7，5，6，4，5，5，则下列说法错误的是（ ）
A．其平均数为5B．其众数为5
C．其方差为5D．其中位数为5
6．不等式x≤2x+1的解集在数轴上表示正确的是（ ）
A．B．
C．D．
7．如图，AB∥EF，∠C＝90°，则α、β、γ的关系为（ ）
A．β＝α+γB．α+β﹣γ＝90°C．α+β+γ＝180°D．β+γ﹣α＝90°
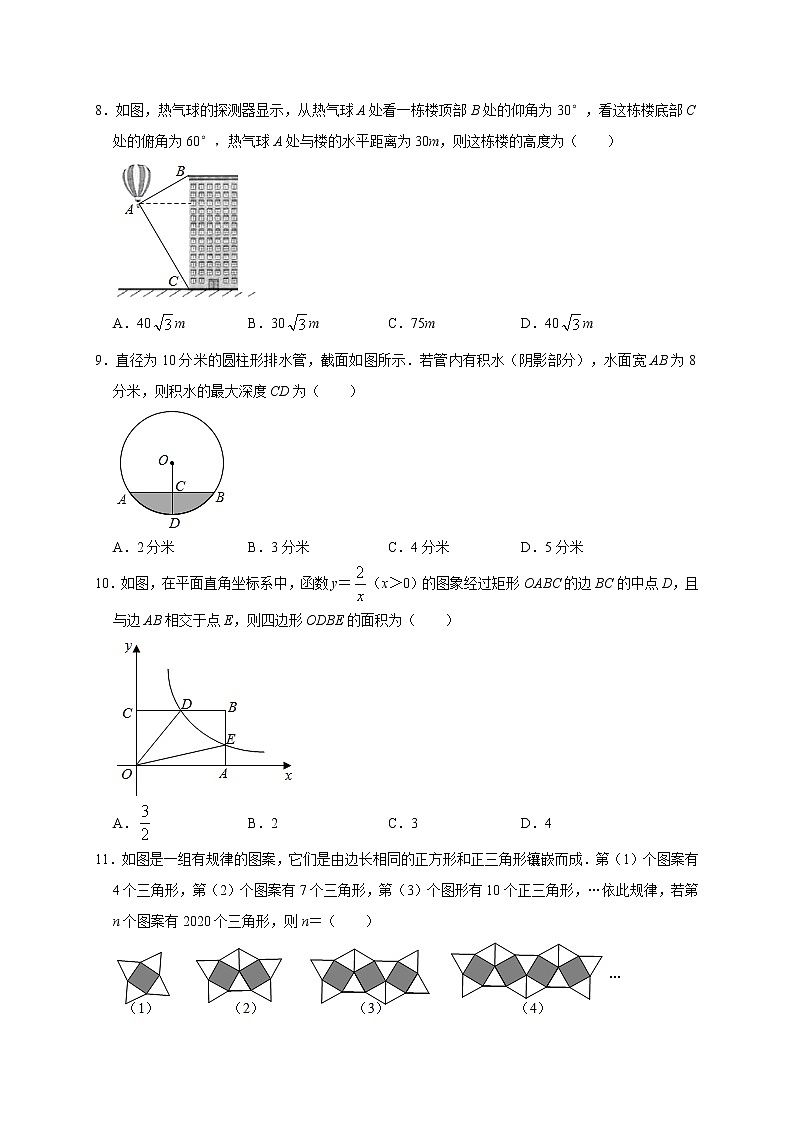
8．如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为30m，则这栋楼的高度为（ ）
A．40mB．30mC．75mD．40m
9．直径为10分米的圆柱形排水管，截面如图所示．若管内有积水（阴影部分），水面宽AB为8分米，则积水的最大深度CD为（ ）
A．2分米B．3分米C．4分米D．5分米
10．如图，在平面直角坐标系中，函数y＝（x＞0）的图象经过矩形OABC的边BC的中点D，且与边AB相交于点E，则四边形ODBE的面积为（ ）
A．B．2C．3D．4
11．如图是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成．第（1）个图案有4个三角形，第（2）个图案有7个三角形，第（3）个图形有10个正三角形，…依此规律，若第n个图案有2020个三角形，则n＝（ ）
A．670B．672C．673D．676
12．已知抛物线y＝ax2+bx+c交x轴于点B （1，0）和点A，交y轴负半轴于点C，且AO＝2CO．有下列结论：①2b+2c＝﹣1；②a＝；③＞0；④4ac+2b+1＝0．其中，正确结论的个数是（ ）
A．1B．2C．3D．4
二．填空题（共6小题，满分18分，每小题3分）
13．若有意义，则x的取值范围是 ．
14．若点P（m﹣1，5）与点Q（3，2﹣n）关于原点成中心对称，则m+n的值是 ．
15．已知x﹣2y＝5，那么代数式3﹣2x+4y的值是 ．
16．形状大小一样、背面相同的四张卡片，其中三张卡片正面分别标有数字“2”“3”“4”，小明和小亮各抽一张，前一个人随机抽一张记下数字后放回，混合均匀，后一个人再随机抽一张记下数字算一次，如果两人抽一次的数字之和是8的概率为，则第四张卡片正面标的数字是 ．
17．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，AB＝OB，点E，F分别是OA，OD的中点，连接EF，EM⊥BC于点M，EM交BD于点N，若∠CEF＝45°，FN＝5，则线段BC的长为 ．
18．秋天到了，花溪区高坡乡美景如画，其中露营基地吸引了不少露营爱好者，露营基地为了接待30名露营爱好者，需要搭建可容纳3人或2人的帐篷若干，若所搭建的帐篷恰好能容纳这30名露营爱好者，则不同的搭建方案有 种．
三．解答题（共2小题，满分12分，每小题6分）
19．（6分）计算：6sin45°+|﹣7|﹣（）﹣3+（2020﹣）0．
20．（6分）（1）已知：当x＝﹣2时，二次三项式2x2+mx+4的值等于18，当x为何值时，这个二次三项式的值是4．
（2）已知关于x的方程x2﹣6x+m2﹣3m﹣5＝0的一个根﹣1，求另一根与m的值．
四．解答题（共2小题，满分16分，每小题8分）
21．（8分）某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制成如图1、图2两幅均不完整的统计图表：
请您根据图表中提供的信息回答下列问题：
（1）统计表中的a＝ ，b＝ ；
（2）小明和小亮参加校本课程学习，若每人从“A”、“B”、“C”三门校本课程中随机选取一门．
请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．
22．（8分）脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB所在的直线，为了测量房屋的高度，在地面上C点测得屋顶A的仰角为35°，此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线，继续向房屋方向走6m到达点D时，又测得屋檐E点的仰角为60°，房屋的顶层横梁EF＝12m，EF∥CB，AB交EF于点G（点C，D，B在同一水平线上）．（参考数据：sin35°≈0.6，cs35°≈0.8，tan35°≈0.7）
（1）求屋顶到横梁的距离AG；
（2）求房屋的高AB（结果精确到1m）．
五．解答题（共2小题，满分18分，每小题9分）
23．（9分）5月18日，我市九年级学生安全有序开学复课．为切实做好疫情防控工作，开学前夕，我市某校准备在民联药店购买口罩和水银体温计发放给每个学生．已知每盒口罩有100只，每盒水银体温计有10支，每盒口罩价格比每盒水银体温计价格多150元．用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同．
（1）求每盒口罩和每盒水银体温计的价格各是多少元？
（2）如果给每位学生发放2只口罩和1支水银体温计，且口罩和水银体温计均整盒购买．设购买口罩m盒（m为正整数），则购买水银体温计多少盒能和口罩刚好配套？请用含m的代数式表示．
（3）在民联药店累计购医用品超过1800元后，超出1800元的部分可享受8折优惠．该校按（2）中的配套方案购买，共支付w元，求w关于m的函数关系式．若该校九年级有900名学生，需要购买口罩和水银体温计各多少盒？所需总费用为多少元？
24．（9分）如图，△ABC中，AB＝AC，以AC为直径的⊙O交BC于点D，点E为AC延长线上一点，且∠BAC＝2∠CDE．
（1）求证：DE是⊙O的切线；
（2）若csB＝，CE＝2，求DE．
六．解答题（共2小题，满分20分，每小题10分）
25．（10分）如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD，BC于点E，F，作BH⊥AF于点H，分别交AC，CD于点G，P，连接GE，GF．
（1）求证：△OAE≌△OBG；
（2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由；
（3）试求：的值（结果保留根号）．
26．（10分）如图所示，抛物线y＝x2﹣2x﹣3与x轴相交于A、B两点，与y轴相交于点C，点M为抛物线的顶点．
（1）求点C及顶点M的坐标．
（2）若点N是第四象限内抛物线上的一个动点，连接BN、CN，求△BCN面积的最大值及此时点N的坐标．
（3）若点D是抛物线对称轴上的动点，点G是抛物线上的动点，是否存在以点B、C、D、G为顶点的四边形是平行四边形．若存在，求出点G的坐标；若不存在，试说明理由．
（4）直线CM交x轴于点E，若点P是线段EM上的一个动点，是否存在以点P、E、O为顶点的三角形与△ABC相似．若存在，求出点P的坐标；若不存在，请说明理由．
校本课程
频数
频率
A
36
0.45
B
0.25
C
16
b
D
8
合计
a
1