



初中数学沪科版七年级下册6.1 平方根 、立方根说课课件ppt
展开请你说一说解决问题的思路.
学校要举行美术作品比赛, 小鸥想裁出一块面积为25 dm2的正方形画布, 画上自己的得意之作参加比赛, 这块正方形画布的边长应取多少?
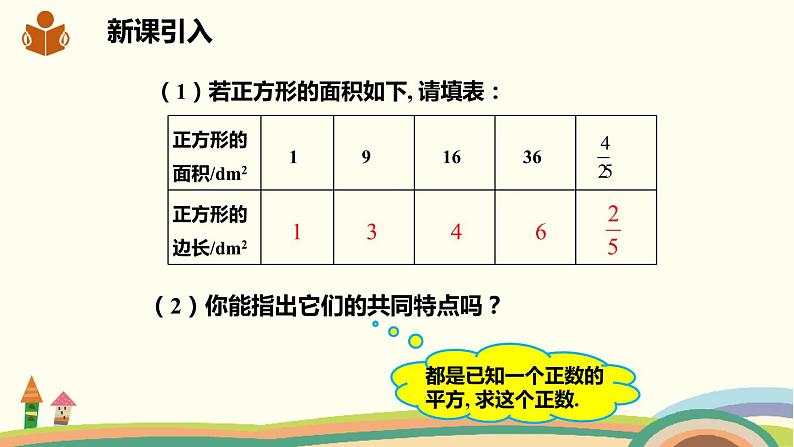
(1)若正方形的面积如下, 请填表:
(2)你能指出它们的共同特点吗?
如果一个数的平方等于9, 这个数是多少?
由于 ,所以这个数是3或-3.
活动1: 探究平方根的概念、性质及求法
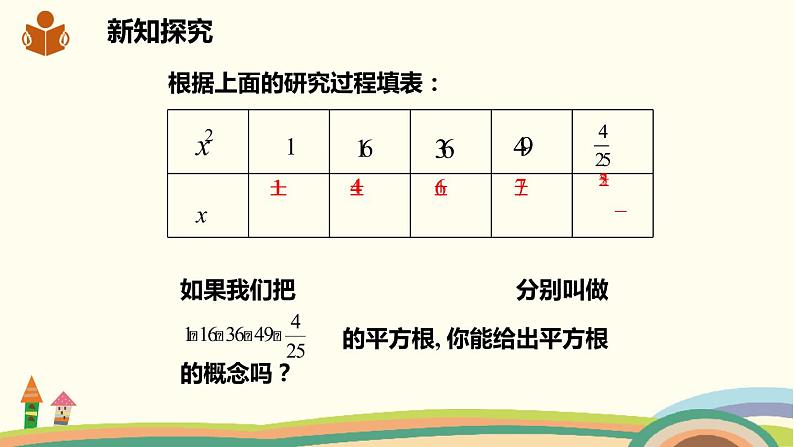
根据上面的研究过程填表:
如果我们把 分别叫做 的平方根, 你能给出平方根的概念吗?
一般地, 如果一个数的平方等于a, 那么这个数叫做a 的平方根或二次方根. 这就是说, 如果 , 那么 x 叫做 a 的平方根.
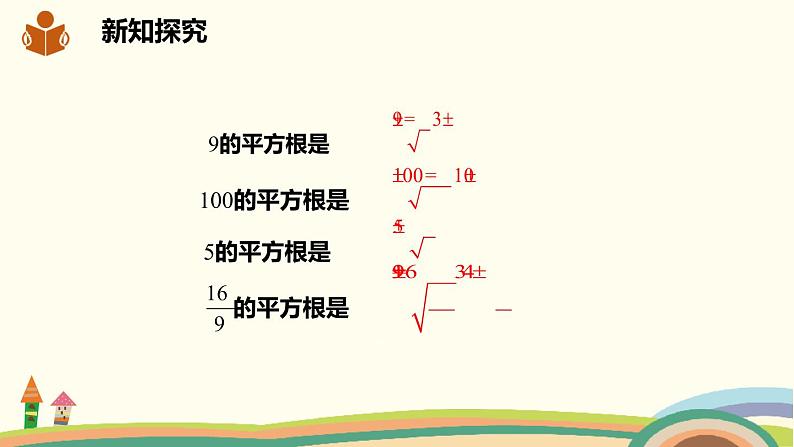
的平方根是
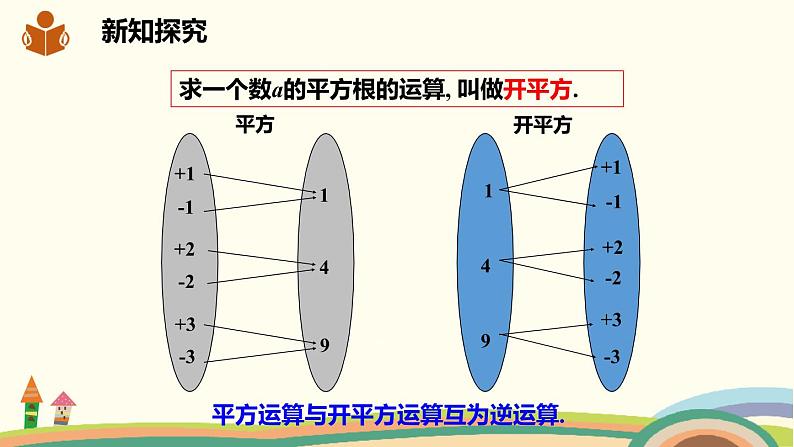
求一个数a的平方根的运算, 叫做开平方.
平方运算与开平方运算互为逆运算.
例1: 下列各数有平方根吗?如果有, 求出它的平方根, 如 果没有, 说明道理. (1)64; (2) ; (3)0.000196; (4)-81.
(3)因为(0.014)2 =0.000196, 所以0.000196的平方根是±0.014, 即 .
(4)因为没有任何数的平方等于-81, 所以-81 没有平方根.
因为02=0, 且任何不为0的数的平方都不等于0, 所以0的平方根只有一个, 它就是0本身. 即 .负数有平方根吗?因为正、负、0的平方都不是负数, 所以负数没有平方根.如: 无意义.
从上面看到, 正数的平方根有两个, 同学们能发现这两个数之间的关系吗?
正数的两个平方根互为相反数.
例: a的一个平方根是5, 则另一个平方根是 , a= .其中____是算术平方根.
我们把正数的正的平方根叫做算术平方根.
活动2: 探究算术平方根的概念、性质及求法
一个正数 x 的平方等于a,即 x2= a, 这个正数 x 叫做a的算术平方根.
x2 = a (x为正数)
规定0的算术平方根是0, 记作 .
也就是说, 非负数的 “算术” 平方根是非负数; 负数不存在算术平方根, 即当 时, 无意义.
例2:一个正数的平方根是2a+3和a-6,你能知道a是多少吗?这个正数又是什么?
解: 由平方根的意义可知 (2a+3)+(a-6)=0, 得 a=1, 所以这个正数是25.
解:(1)依次按键 3136 显示: 56. 所以 .
(2) 依次按键 2 显示: 1.414213562. 所以 .
例 用计算器求下列各式的值: (1) ; (2) (精确到 ).
活动3: 探究用计算器求平方根
一般地, 如果一个数的平方等于a, 那么这个数叫做a的平方根或二次方根. 这就是说, 如果 , 那么 x 叫做a的平方根. 正数的两个平方根互为相反数.
0的平方根只有一个, 它就是0本身. 负数没有平方根.
一个正数 x的平方等于a, 即x2 = a, 这个正数 x叫做a的算术平方根.
(1)9的算数平方根是 ;
(2) 的算数平方根是 ;
(3)0.01的算数平方根是 ;
(4)10-6 的算数平方根是 ;
(5)(-4)2的算数平方根是 ;
(6)10的算数平方根是 .
2.你知道下列各式中字母x的取值范围吗?
初中数学人教版七年级下册6.1 平方根一等奖课件ppt: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c77684_t3/?tag_id=26" target="_blank">6.1 平方根一等奖课件ppt</a>,共25页。PPT课件主要包含了素养目标,课堂导入,知识点1算术平方根,新知探究,a的算术平方根,互为逆运算,平方根号,被开方数a≥0,读作“根号a”,x≥0等内容,欢迎下载使用。
沪科版七年级下册6.1 平方根 、立方根教学课件ppt: 这是一份沪科版七年级下册6.1 平方根 、立方根教学课件ppt,共27页。PPT课件主要包含了知识要点,算术平方根的应用,0的平方根是0,-9没有平方根,开平方,按键顺序,解1依次按键,显示结果为56所以,解2依次按键等内容,欢迎下载使用。
数学七年级下册6.1 平方根 、立方根教学课件ppt: 这是一份数学七年级下册6.1 平方根 、立方根教学课件ppt,共18页。PPT课件主要包含了5-42,的算术平方根是__等内容,欢迎下载使用。













