

全国版高考数学必刷题:第十七单元 直线与圆锥曲线的关系
展开第十七单元 直线与圆锥曲线的关系
考点一
直线与椭圆的综合应用
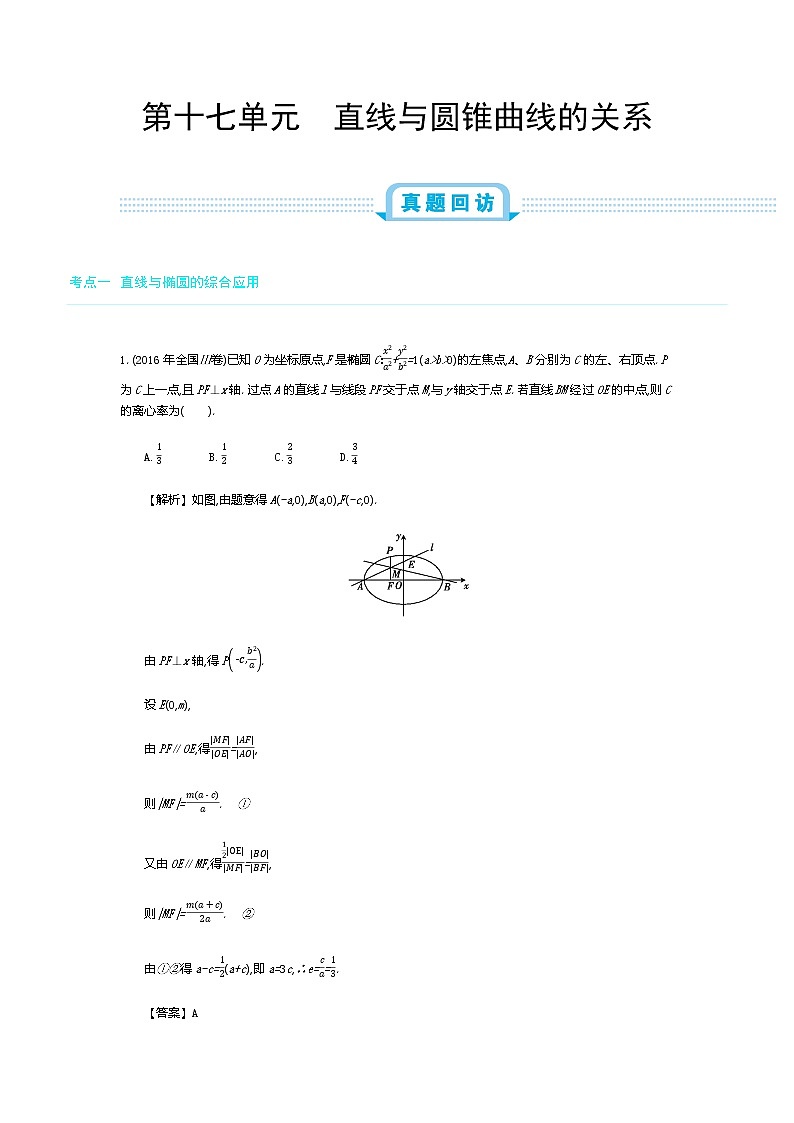
1.(2016年全国Ⅲ卷)已知O为坐标原点,F是椭圆C:x2a2+y2b2=1(a>b>0)的左焦点,A、B分别为C的左、右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( ).
A.13 B.12 C.23 D.34
【解析】如图,由题意得A(-a,0),B(a,0),F(-c,0).
由PF⊥x轴,得P-c,b2a.
设E(0,m),
由PF∥OE,得|MF||OE|=|AF||AO|,
则|MF|=m(a-c)a. ①
又由OE∥MF,得12|OE||MF|=|BO||BF|,
则|MF|=m(a+c)2a. ②
由①②得a-c=12(a+c),即a=3c,∴e=ca=13.
【答案】A
2.(2014年全国Ⅱ卷)设F1、F2分别是椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为34,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
【解析】(1)由c=a2-b2及题设知Mc,b2a,2b2=3ac.
将b2=a2-c2代入2b2=3ac,
解得ca=12或ca=-2(舍去).
故C的离心率为12.
(2)由题意知,原点O为F1F2的中点,MF2∥y轴,
所以直线MF1与y轴的交点D(0,2)是线段MF1的中点,
故b2a=4,即b2=4a. ①
由|MN|=5|F1N|,得|DF1|=2|F1N|.设N(x1,y1),由题意知y1<0,则
2(-c-x1)=c,-2y1=2,即x1=-32c,y1=-1.
代入C的方程,得9c24a2+1b2=1. ②
将①及c=a2-b2代入②,得9(a2-4a)4a2+14a=1,
解得a=7,b2=4a=28,
故a=7,b=27.
3.(2017年全国Ⅰ卷)已知椭圆C:x2a2+y2b2=1(a>b>0),四点P1(1,1),P2(0,1),P3-1,32,P41,32中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
【解析】(1)由于P3,P4两点关于y轴对称,故由题设知椭圆C经过P3,P4两点.
又由1a2+1b2>1a2+34b2知,椭圆C不经过点P1,所以点P2在椭圆C上.
因此1b2=1,1a2+34b2=1,解得a2=4,b2=1.
故C的方程为x24+y2=1.
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知t≠0,且|t|<2,可得A,B两点的坐标分别为t,4-t22,t,-4-t22.
则k1+k2=4-t2-22t-4-t2+22t=-1,得t=2,不符合题设.
从而可设l:y=kx+m(m≠1),将y=kx+m代入x24+y2=1,得(4k2+1)x2+8kmx+4m2-4=0,
由题设可知Δ=16(4k2-m2+1)>0.
设A(x1,y1),B(x2,y2),则x1+x2=-8km4k2+1,x1x2=4m2-44k2+1.
而k1+k2=y1-1x1+y2-1x2
=kx1+m-1x1+kx2+m-1x2
=2kx1x2+(m-1)(x1+x2)x1x2.
由题设k1+k2=-1,故(2k+1)x1x2+(m-1)(x1+x2)=0.
即(2k+1)·4m2-44k2+1+(m-1)·-8km4k2+1=0.
解得k=-m+12.
当且仅当m>-1时,Δ>0.所以l:y=-m+12x+m,即y+1=-m+12(x-2),
所以l过定点(2,-1).
4.(2015年全国Ⅱ卷)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值.
(2)若l过点m3,m,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
【解析】(1)根据题意,因为直线不平行于坐标轴,所以斜率k必然存在,
故设直线l:y=kx+b(k≠0,b≠0),则A(x1,y1),B(x2,y2),M(xM,yM).
将y=kx+b代入9x2+y2=m2,得(k2+9)x2+2kbx+b2-m2=0,
故xM=x1+x22=-kbk2+9,yM=kxM+b=9bk2+9.
于是直线OM的斜率kOM=yMxM=-9k,即kOM·k=-9.
所以直线OM的斜率与l的斜率的乘积为定值.
(2)不妨设四边形OAPB能为平行四边形.
因为直线l过点m3,m,所以l不过原点且与C有两个交点的充要条件是k>0,且k≠3.
由(1)得OM的方程为y=-9kx.设点P的横坐标为xP.
由y=-9kx,9x2+y2=m2,得xP2=k2m29k2+81,即xP=±km3k2+9.
将点m3,m的坐标代入直线l的方程,得b=m(3-k)3,因此xM=k(k-3)m3(k2+9).
四边形OAPB为平行四边形,当且仅当线段AB与线段OP互相平分,
即xP=2xM.于是±km3k2+9=2×k(k-3)m3(k2+9).
解得k1=4-7,k2=4+7.
因为ki>0,ki≠3,i=1,2,
所以当l的斜率为4-7或4+7时,四边形OAPB为平行四边形.
5.(2016年全国Ⅱ卷)已知椭圆E:x2t+y23=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(1)当t=4,|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,求k的取值范围.
【解析】(1)设M(x1,y1),则由题意知y1>0.
当t=4时,椭圆E的方程为x24+y23=1,A(-2,0).
由已知及椭圆的对称性知,直线AM的倾斜角为π4,
因此直线AM的方程为y=x+2.
将x=y-2代入x24+y23=1,得7y2-12y=0,
解得y=0或y=127,所以y1=127.
因此△AMN的面积S△AMN=2×12×127×127=14449.
(2)由题意知t>3,k>0,A(-t,0).将直线AM的方程y=k(x+t)代入x2t+y23=1,
得(3+tk2)x2+2t·tk2x+t2k2-3t=0.
由x1·(-t)=t2k2-3t3+tk2,
得x1=t(3-tk2)3+tk2,
故|AM|=|x1+t|1+k2=6t(1+k2)3+tk2.
由题设知,直线AN的方程为y=-1k(x+t),故同理可得|AN|=6kt(1+k2)3k2+t.
由2|AM|=|AN|,
得23+tk2=k3k2+t,即(k3-2)t=3k(2k-1).
当k=32时上式不成立,因此t=3k(2k-1)k3-2.
t>3等价于k3-2k2+k-2k3-2=(k-2)(k2+1)k3-2<0,即k-2k3-2<0,
由此得k-2>0,k3-2<0或k-2<0,k3-2>0,解得32
考点二
直线与抛物线的综合应用
6.(2017年全国Ⅰ卷)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( ).
A.16 B.14 C.12 D.10
【解析】设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),直线l1的方程为y=k1(x-1),与抛物线方程y2=4x联立,得k12x2-(2k12+4)x+k12=0,所以x1+x2=2k12+4k12.
同理l2与抛物线交点x3+x4=2k22+4k22.
由抛物线定义可得|AB|+|CD|=x1+x2+x3+x4+2p=2k12+4k12+2k22+4k22+4=4k12+4k22+8≥216k12k22+8=16.
当且仅当k1=-k2=1或k1=-k2=-1时取等号.
【答案】A
7.(2015年全国Ⅰ卷)在直角坐标系xOy中,曲线C:y=x24与直线l:y=kx+a(a>0)交于M,N两点.
(1)当k=0时,分别求C在点M和N处的切线方程.
(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
【解析】(1)由题设可得M(2a,a),N(-2a,a)或M(-2a,a),N(2a,a).
又因为y'=x2,所以y=x24在x=2a处的导数值为a,C在点(2a,a)处的切线方程为y-a=a(x-2a),
即ax-y-a=0.
y=x24在x=-2a处的导数值为-a,C在点(-2a,a)处的切线方程为y-a=-a(x+2a),
即ax+y+a=0.
故所求切线方程为ax-y-a=0和ax+y+a=0.
(2)存在符合题意的点.证明如下:
设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为k1,k2.
将y=kx+a代入C的方程,得x2-4kx-4a=0.
故x1+x2=4k,x1x2=-4a.
从而k1+k2=y1-bx1+y2-bx2
=2kx1x2+(a-b)(x1+x2)x1x2=k(a+b)a.
当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,
故∠OPM=∠OPN,所以点P(0,-a)符合题意.
8.(2017年全国Ⅲ卷)已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
【解析】(1)设A(x1,y1),B(x2,y2),l:x=my+2,
由x=my+2,y2=2x,可得y2-2my-4=0,则y1y2=-4.
又x1=y122,x2=y222,故x1x2=(y1y2)24=4.
因此OA的斜率与OB的斜率之积为y1x1·y2x2=-44=-1.
所以OA⊥OB,故坐标原点O在圆M上.
(2)由(1)可得y1+y2=2m,x1+x2=m(y1+y2)+4=2m2+4,
故圆心M的坐标为(m2+2,m),圆M的半径r=(m2+2)2+m2.
由于圆M过点P(4,-2),因此AP·BP=0,
故(x1-4)(x2-4)+(y1+2)(y2+2)=0,
(也可结论:以AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,直接写出)
即x1x2-4(x1+x2)+y1y2+2(y1+y2)+20=0.
由(1)可得,y1y2=-4,x1x2=4,
所以2m2-m-1=0,解得m=1或m=-12.
当m=1时,直线l的方程为x-y-2=0,圆心M的坐标为(3,1),圆M的半径为10,圆M的方程为(x-3)2+(y-1)2=10.
当m=-12时,直线l的方程为2x+y-4=0,圆心M的坐标为94,-12,圆M的半径为854,圆M的方程为x-942+y+122=8516.
9.(2016年全国Ⅲ卷)已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
【解析】由题意知F12,0.设l1:y=a,l2:y=b,则ab≠0,且Aa22,a,Bb22,b,P-12,a,Q-12,b,R-12,a+b2.
记过A,B两点的直线为l,
则l的方程为2x-(a+b)y+ab=0.
(1)由于点F在线段AB上,故1+ab=0.
记AR的斜率为k1,FQ的斜率为k2,则
k1=a-b1+a2=a-ba2-ab=1a=-aba=-b=b-0-12-12=k2.
所以AR∥FQ.
(2)设l与x轴的交点为D(x1,0),
则S△ABF=12|b-a||FD|=12|b-a|x1-12,
S△PQF=|a-b|2.
由题设可得|b-a|x1-12=|a-b|2,
所以x1=0(舍去)或x1=1.
设满足条件的AB的中点为E(x,y),
当AB与x轴不垂直时,
由kAB=kDE,可得2a+b=yx-1(x≠1).
而a+b2=y,所以y2=x-1(x≠1).
当AB与x轴垂直时,E与D重合,此时E点坐标为(1,0),满足方程y2=x-1.
故所求轨迹方程为y2=x-1.
考点三
直线、圆与圆锥曲线的综合
10.(2017年全国Ⅱ卷)设O为坐标原点,动点M在椭圆C:x22+y2=1上,过M作x轴的垂线,垂足为N,点P满足NP=2NM.
(1)求点P的轨迹方程;
(2)设点Q在直线x=-3上,且OP·PQ=1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
【解析】(1)设P(x,y),M(x0,y0),则N(x0,0),NP=(x-x0,y),NM=(0,y0).
由NP=2 NM ,得(x-x0,y)=2(0,y0),
即x-x0=0,y=2y0,解得x0=x,y0=y2,
代入椭圆方程x022+y02=1,得x2+y2=2,
故点P的轨迹方程为x2+y2=2.
(2)由题意知F(-1,0),设Q(-3,t),P(m,n),则
OQ=(-3,t),PF=(-1-m,-n),OQ·PF=3+3m-tn,OP=(m,n),PQ=(-3-m,t-n).
由OP·PQ=1,得-3m-m2+tn-n2=1,
又由(1)知m2+n2=2,故3+3m-tn=0.
所以OQ·PF=0,即OQ⊥PF.
又过点P存在唯一直线垂直于OQ,
所以过点P且垂直于OQ的直线l过C的左焦点F.
11.(2013年全国Ⅰ卷)已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
【解析】由已知得圆M的圆心为M(-1,0),半径r1=1;
圆N的圆心为N(1,0),半径r2=3.
设圆P的圆心为P(x,y),半径为R.
(1)因为圆P与圆M外切并且与圆N内切,
所以|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4.
由椭圆的定义可知,曲线C是以M,N为左、右焦点,长半轴长为2,短半轴长为3的椭圆(左顶点除外),其方程为x24+y23=1(x≠-2).
(2)对于曲线C上任意一点P(x,y),因为|PM|-|PN|=2R-2≤2,所以R≤2,
当且仅当圆P的圆心为(2,0)时,R=2.
所以当圆P的半径最长时,其方程为(x-2)2+y2=4.
若l的倾斜角为90°,则l与y轴重合,可得|AB|=23.
若l的倾斜角不为90°,由r1≠R知l不平行于x轴,
设l与x轴的交点为Q,则|QP||QM|=Rr1,可求得Q(-4,0),
所以可设l:y=k(x+4),由l与圆M相切得|3k|1+k2=1,解得k=±24.
当k=24时,y=24x+2代入x24+y23=1并整理,得7x2+8x-8=0,
解得x1,2=4±627.所以|AB|=1+k2|x2-x1|=187.
当k=-24时,由图形的对称性可知|AB|=187.
综上,|AB|=23或|AB|=187.
12.(2016年全国Ⅰ卷)设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
【解析】(1)如图,圆A的圆心为A(-1,0),半径R=4,
因为BE∥AC,所以∠C=∠EBD.又因为AC=AD,所以∠C=∠EDB,
于是∠EBD=∠EDB,所以|EB|=|ED|.故|AE|+|EB|=|AE|+|ED|=|AD|=4为定值.
因为|AB|=2,点E的轨迹是以A,B为焦点,长轴长为4的椭圆,
由c=1,a=2,得b2=3,
所以点E的轨迹方程为x24+y23=1(y≠0).
(2)因为直线l与x轴不重合,故可设l的方程为x=my+1,
过点B且与l垂直的直线方程为y=m(x-1).
由x24+y23=1,x=my+1,得(3m2+4)y2+6my-9=0.
设M(x1,y1),N(x2,y2),则y1+y2=-6m3m2+4,y1·y2=-93m2+4.
得|MN|=m2+1·-6m3m2+42-4-93m2+4=12(m2+1)3m2+4.
由x2+y2+2x-15=0,y=m(x-1),得(m2+1)x2-2(m2-1)x+m2-15=0.
设P(x3,y3),Q(x4,y4),则x3+x4=2(m2-1)m2+1,x3·x4=m2-15m2+1.
得|PQ|=m2+1·2(m2-1)m2+12-4m2-15m2+1=43m2+4m2+1.
四边形MPNQ的面积S=12|MN|·|PQ|=24m2+13m2+4=2413-13m2+12,
因为m2≥0,所以0<13m2+12≤112,故12≤S<83.
即四边形MPNQ面积的取值范围是[12,83).
高频考点:直线与圆锥曲线的位置关系及弦长、中点弦问题,最值、取值范围、证明问题,定点、定值、探索性问题.
命题特点:主要考查解答题,分数为12分,常常以不同曲线(圆、椭圆、抛物线)的位置关系为基础设计“连环题”,结合曲线的定义及几何性质,利用待定系数法先确定曲线的标准方程,再进一步研究弦长、图形面积、最值、取值范围等,题目综合性较强,往往与向量(共线、垂直、数量积)结合,涉及方程组的联立、根的判别式、根与系数的关系等.
§17.1 直线与圆锥曲线的位置关系
一
直线与圆锥曲线的位置关系
判断直线l与圆锥曲线C的位置关系时,通常将直线l的方程Ax+By+C=0(A,B不同时为0)代入圆锥曲线C的方程F(x,y)=0,消去y(也可以消去x)得到一个关于变量x(或变量y)的一元二次方程.
即Ax+By+C=0,F(x,y)=0消去y,得ax2+bx+c=0.
(1)当a≠0时,设一元二次方程ax2+bx+c=0的判别式为Δ,则Δ>0⇔直线与圆锥曲线C ;
Δ=0⇔直线与圆锥曲线C ;
Δ<0⇔直线与圆锥曲线C .
(2)当a=0,b≠0时,即得到一个一元一次方程,则直线l与圆锥曲线C相交,且只有一个交点,此时,若C为双曲线,则直线l与双曲线的渐近线的位置关系是 ;若C为抛物线,则直线l与抛物线的对称轴的位置关系是 .
☞左学右考
1 判断下列结论是否正确,正确的在括号内画“√”,错误的画“×”.
(1)直线l与双曲线C相切的充要条件是直线l与双曲线C只有一个公共点.( )
(2)经过抛物线上一点有且只有一条直线与抛物线有一个公共点.( )
(3)直线y=kx+1与椭圆x25+y29=1恒有两个公共点.( )
(4)过抛物线y2=2px(p>0)的焦点的弦中,最短的弦长是2p.( )
(5)过椭圆x2a2+y2b2=1的焦点的弦中,最短的弦长为2b2a.( )
二
圆锥曲线的弦长
设斜率为k(k≠0)的直线l与圆锥曲线C相交于A,B两点,A(x1,y1),B(x2,y2),则
|AB|=1+k2|x1-x2|=1+k2·(x1+x2)2-4x1x2
=1+1k2·|y1-y2|=1+1k2·(y1+y2)2-4y1y2.
三
直线与圆锥曲线相交弦的中点问题
中点弦问题常用“根与系数的关系”或“点差法”求解.
(1)利用根与系数的关系:将直线方程代入圆锥曲线的方程,消元后得到一个一元二次方程,利用根与系数的关系和中点坐标公式建立等式求解,注意不能忽视对判别式的讨论.
(2)点差法:若直线l与圆锥曲线C有两个交点A,B,一般地,首先设出A(x1,y1),B(x2,y2),代入曲线方程,通过作差,构造出x1+x2,y1+y2,x1-x2,y1-y2,从而建立中点坐标和斜率的关系.
四
辨明两个易误点
(1)直线与双曲线交于一点时,易误认为直线与双曲线相切,事实上不一定相切,当直线与双曲线的渐近线平行时,直线与双曲线也相交于一点.
(2)直线与抛物线交于一点时,除直线与抛物线相切外,易忽视直线与抛物线的对称轴平行或重合时也相交于一点.
2 若直线y=kx与双曲线x2-y2=2相交,则k的取值范围是( ).
A.(0,1) B.(-2,2)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
3 过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( ).
A.1条 B.2条
C.3条 D.4条
4 直线y=x+1被椭圆x2+2y2=4所截得的弦的中点坐标是( ).
A.13,-23
B.-23,13
C.12,-13
D.-13,12
5 (教材习题)点P是椭圆16x2+25y2=1600上的一点,F1、F2是椭圆的两个焦点,又知点P在x轴的上方,F2是椭圆的右焦点,直线PF2的斜率为-43,则△PF1F2的面积为 .
知识清单
一、(1)相交 相切 相离 (2)平行 平行或重合
基础训练
1.【答案】(1)× (2)× (3)√ (4)√ (5)√
2.【解析】双曲线x2-y2=2的渐近线方程为y=±x,若直线与双曲线相交,由数形结合,得k∈(-1,1).故选C.
【答案】C
3.【解析】过点(0,1)的直线与抛物线相切时有两条,又与对称轴平行的直线y=1与抛物线也只有一个公共点,故满足条件的直线有3条.
【答案】C
4.【解析】联立y=x+1,x2+2y2=4,得x2+2(x+1)2-4=0,即3x2+4x-2=0,则弦的中点的横坐标为-23,纵坐标为-23+1=13,即-23,13,故选B.
【答案】B
5.【解析】椭圆的标准方程为x2100+y264=1,则F1(-6,0),F2(6,0),故直线PF2的方程为y=-43(x-6).将直线方程代入16x2+25y2=1600,得19x2-225x+650=0,解得x1=5或x2=13019.当x2=13019时,y2<0.由x1=5,得y1=43,故S△PF1F2=12F1F2|y1|=12×12×43=243.
【答案】243
题型一
直线与圆锥曲线位置关系的判定及应用
【例1】(2017宜昌一中检测)设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率k的取值范围是( ).
A.-12,12 B.[-2,2] C.[-1,1] D.[-4,4]
【解析】由题意可知y2=8x的准线为x=-2,所以点Q的坐标为(-2,0).
当直线l的斜率k=0时,直线与抛物线的交点为(0,0);
当直线l的斜率k≠0时,设直线l的方程为y=k(x+2)(斜率k显然存在),
联立y=k(x+2),y2=8x,得k2x2+4(k2-2)x+4k2=0,由Δ=[4(k2-2)]2-4×(4k2)×k2≥0,得-1≤k≤1且k≠0.
综上可知,k的取值范围是[-1,1].故选C.
【答案】C
在讨论直线和圆锥曲线的位置关系时,先联立方程组,再消去x或y,得到关于y或x的方程.如果是直线与圆或椭圆,那么所得方程一定为一元二次方程;如果是直线与双曲线或抛物线,那么需讨论二次项系数等于零和不等于零两种情况.只有一元二次方程才有判别式,另外还应注意讨论斜率不存在的情形.有时根据定点与圆锥曲线的位置关系判定直线与圆锥曲线的关系.
【变式训练1】(1)(2017兰州检测)若直线mx+ny=4与圆O:x2+y2=4没有交点,则过点(m,n)的直线与椭圆x29+y24=1的交点个数为( ).
A.3 B.2 C.1 D.0
(2)若直线y=kx+2与双曲线x2-y2=6的右支交于不同的两点,则k的取值范围是( ).
A.-153,153 B.0,153
C.-153,0 D.-153,-1
【解析】(1)∵直线mx+ny=4和圆O:x2+y2=4没有交点,∴4m2+n2>2,即m2+n2<4.
∴m29+n24
∴过点(m,n)的直线与椭圆x29+y24=1的交点有2个.故选B.
(2)(法一)由y=kx+2,x2-y2=6,得(1-k2)x2-4kx-10=0,
∵直线与双曲线右支有两个不同交点,
∴1-k2≠0,Δ=16k2-4(1-k2)×(-10)>0,x1+x2=4k1-k2>0,x1x2=-101-k2>0,
解得-153
当k=-1时,直线与双曲线的渐近线平行,顺时针旋转直线y=-x+2时,直线与双曲线右支有两个交点,
∴k的取值范围为-153
题型二
中点问题
【例2】中心在原点,焦点在x轴上的双曲线C的离心率为2,直线l与双曲线C交于A,B两点,线段AB的中点M在第一象限,并且在抛物线y2=2px(p>0)上,且点M到抛物线焦点的距离为p,则直线l的斜率为( ).
A.1 B.2 C.32 D.52
【解析】因为中心在原点,焦点在x轴上的双曲线C的离心率为2,所以1+b2a2=2,即ba=3,所以双曲线方程为x2a2-y23a2=1.因为第一象限内的点M到抛物线y2=2px焦点的距离为p,故点M的坐标为p2,p.
(法一)由题意知直线l的斜率存在,设直线l:y-p=kx-p2,联立y-p=kx-p2,x2a2-y23a2=1,得(3-k2)x2-(2kp-k2p)x-k2p24-p2+kp2-3a2=0.
设A(x1,y1),B(x2,y2),则x1+x2=2kp-k2p3-k2.
又因为x1+x22=p2,
所以2kp-k2p3-k2=p,解得k=32.
(法二)设A(x1,y1),B(x2,y2),代入双曲线方程得x12a2-y123a2=1,x22a2-y223a2=1,
两式相减,得y1-y2x1-x2=3(x1+x2)y1+y2,依题意x1+x2=p,y1+y2=2p,
所以直线l的斜率k=y1-y2x1-x2=3(x1+x2)y1+y2=32.故选C.
【答案】C
求解直线与圆锥曲线相交所得弦的中点问题主要有两种方法:一是联立直线与圆锥曲线方程,消去x或y后得到一个一元二次方程,最后结合韦达定理求解;二是除中点外,还涉及直线的斜率,一般采用“点差法”求解可减少运算量.
【变式训练2】(1)已知抛物线C的顶点在坐标原点,准线方程为x=-1,直线l与抛物线C相交于A,B两点.若线段AB的中点为(2,1),则直线l的方程为( ).
A.y=2x-3 B.y=-2x+5
C.y=-x+3 D.y=x-1
(2)已知点(4,2)是直线l被椭圆x236+y29=1所截得的线段的中点,则直线l的方程是 .
【解析】(1)设抛物线的方程为y2=2px(p>0),则p2=1,所以抛物线的方程为y2=4x.设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2,两式相减,得(y1+y2)(y1-y2)=4(x1-x2),所以直线l的斜率为k=y1-y2x1-x2=4y1+y2=2,所以直线l的方程为y-1=2(x-2),即y=2x-3.故选A.
(2)设直线l与椭圆交于A(x1,y1),B(x2,y2),则x1236+y129=1,x2236+y229=1,两式相减,得y1-y2x1-x2=-x1+x24(y1+y2).
又因为x1+x2=8,y1+y2=4,所以y1-y2x1-x2=-12,
故直线l的方程为y-2=-12(x-4),即x+2y-8=0.
【答案】(1)A (2)x+2y-8=0
题型三
弦长与面积问题
【例3】(2017凉山一诊)设椭圆E:x2a2+y2b2=1(a>b>0)的离心率为12,E上一点P到右焦点距离的最小值为1.
(1)求椭圆E的方程;
(2)过点(0,2)且倾斜角为60°的直线交椭圆E于A,B两点,求△AOB的面积.
【解析】(1)由题意得ca=12,且a-c=1,∴a=2,c=1.
∴b2=a2-c2=3,故椭圆E的方程为x24+y23=1.
(2)过点(0,2)的直线l的方程为y=3x+2,
代入椭圆方程x24+y23=1,可得15x2+163x+4=0,Δ>0恒成立.
设A(x1,y1),B(x2,y2),则x1+x2=-16315,x1x2=415,
∴|AB|=1+k2|x1-x2|=2(x1+x2)2-4x1x2=83315.
∵点O到直线AB的距离d=21+k2=1,
∴S△ABC=|AB|2d=43315.
求弦长时可利用弦长公式,根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程,利用根与系数的关系得到两根之和、两根之积的代数式,然后进行整体代入弦长公式求解.
【变式训练3】已知斜率为1的直线l与椭圆x24+y2=1相交于A,B两点,则|AB|的最大值为( ).
A.2 B.455 C.4105 D.8105
【解析】设A,B两点的坐标分别为(x1,y1),(x2,y2),直线l的方程为y=x+t,
由x2+4y2=4,y=x+t,消去y,得5x2+8tx+4(t2-1)=0,则x1+x2=-85t,x1x2=4(t2-1)5.
∴|AB|=1+k2|x1-x2|=1+k2·(x1+x2)2-4x1x2=2·-85t2-4×4(t2-1)5=425·5-t2,当t=0时,|AB|max=4105.
【答案】C
方法
对称问题求解策略
【突破训练】(2015年浙江卷)已知椭圆x22+y2=1上两个不同的点A,B关于直线y=mx+12对称.
(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
【解析】(1)(法一)由题意知m≠0,可设直线AB的方程为y=-1mx+b,
由x22+y2=1,y=-1mx+b,消去y,得12+1m2x2-2bmx+b2-1=0,
∵直线y=-1mx+b与椭圆x22+y2=1有两个不同的交点,
∴Δ=-2b2+2+4m2>0, ①
将AB的中点M2mbm2+2,m2bm2+2代入直线方程y=mx+12,解得b=-m2+22m2, ②
由①②得m<-63或m>63.
(法二)由题意知m≠0,设A(x1,y1),B(x2,y2)是椭圆x22+y2=1上符合条件的两个点,M(x0,y0)是AB的中点,则x122+y12=1,x222+y22=1,
两式相减,得(x1+x2)(x1-x2)2+(y1+y2)(y1-y2)=0.
∴kAB=y1-y2x1-x2=-(x1+x2)2(y1+y2)=-x02y0.
∵点A,B关于直线y=mx+12对称,∴kAB=-x02y0=-1m,即y0=m2x0, ③
又y0=mx0+12, ④
由③④得x0=1m,y0=12.
∵点M(x0,y0)在椭圆内部,∴x022+y02<1,即m2>23,
∴m<-63或m>63.
(2)令t=1m∈-62,0∪0,62,则|AB|=t2+1·-2t4+2t2+32t2+12,
且点O到直线AB的距离为d=t2+12t2+1.
设△AOB的面积为S(t),∴S(t)=12|AB|·d=12-2t2-122+2≤22,
当且仅当t2=12时,等号成立,故△AOB面积的最大值为22.
1.(2017山西质检)设AB为过抛物线y2=2px(p>0)的焦点的弦,则|AB|的最小值为( ).
A.p2 B.p C.2p D.无法确定
【解析】当弦AB垂直于对称轴时,|AB|最短,此时x=p2,∴y=±p,|AB|min=2p.故选C.
【答案】C
2.(2017福州质检)抛物线C的顶点为原点,焦点在x轴上,直线x-y=0与抛物线C交于A,B两点,若P(1,1)为线段AB的中点,则抛物线C的方程为( ).
A.y=2x2 B.y2=2x
C.x2=2y D.y2=-2x
【解析】A,B两点其中一个点的坐标是(0,0),由AB的中点坐标为(1,1),可知另一个点的坐标为(2,2),代入y2=2px中,可得p=1,所以抛物线C的方程为y2=2x.
【答案】B
3.(2017赣州二模)设双曲线x2a2-y2b2=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( ).
A.54 B.5 C.52 D.5
【解析】双曲线x2a2-y2b2=1的一条渐近线为y=bax,联立方程组y=bax,y=x2+1,消去y,得x2-bax+1=0.因为方程有唯一的解,
所以Δ=ba2-4=0,得ba=2.
所以e=ca=a2+b2a=1+ba2=5.选D.
【答案】D
4.(2017太原一模)已知抛物线y2=4x的焦点为F,过焦点F的直线交抛物线于A,B两点,O为坐标原点,若AB=6,则△AOB的面积为( ).
A.6 B.22 C.23 D.4
【解析】设直线AB的方程为y=k(x-1),
与抛物线方程联立可得y2-4ky-4=0,
则y1-y2=41+1k2.
由弦长公式可得1+1k2y1-y2=41+1k2=6,∴k2=2.
∴S△AOB=12×OF×y1-y2=12×1×26=6.故选A.
【答案】A
5.(2017山东质检)已知双曲线C:x24-y25=1的右焦点为F,过点F的直线l与C交于A,B两点,若|AB|=5,则满足条件的l的条数为 .
【解析】因为a2=4,b2=5,c2=9,所以F(3,0).若点A,B都在双曲线的右支上,当AB垂直于x轴时,将x=3代入x24-y25=1,得y=±52,所以|AB|=5,满足题意;若点A,B分别在双曲线的两支上,因为a=2,所以两个顶点的距离为2+2=4<5,所以满足|AB|=5的直线有2条,且关于x轴对称.综上可知,一共有3条.
【答案】3
6.(2017南昌月考)已知双曲线x2a2-y2b2=1(a>0,b>0)与斜率为1的直线交于A,B两点,线段AB的中点为(4,1),则该双曲线的渐近线方程是 .
【解析】设A(x1,y1),B(x2,y2),则x12a2-y12b2=1,x22a2-y22b2=1,两式相减并整理,得y2-y1x2-x1=b2(x2+x1)a2(y2+y1)=4b2a2.∵k=1,∴4b2a2=1,∴ba=±12.故双曲线的渐近线方程为y=±12x.
【答案】y=±12x
7.(2017年北京卷)已知抛物线C:y2=2px过点P(1,1).过点0,12作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
【解析】(1)由抛物线C:y2=2px过点P(1,1),得p=12.所以抛物线C的方程为y2=x,其焦点坐标为14,0,准线方程为x=-14.
(2)(法一)由题意,设直线l的方程为y=kx+12(k≠0),l与抛物线C的交点为M(x1,y1),N(x2,y2).由y=kx+12,y2=x,得4k2x2+(4k-4)x+1=0,则x1+x2=1-kk2,x1x2=14k2.
因为点P的坐标为(1,1),所以直线OP的方程为y=x,点A的坐标为(x1,y1).
因为直线ON的方程为y=y2x2x,所以点B的坐标为x1,y2x1x2.
因为y1+y2x1x2-2x1=y1x2+y2x1-2x1x2x2
=kx1+12x2+kx2+12x1-2x1x2x2
=(2k-2)x1x2+12(x1+x2)x2
=(2k-2)×14k2+1-k2k2x2=0,
所以y1+y2x1x2=2x1.
故A为线段BM的中点.
(法二)要证A为BM的中点,且xA,xB,xM相同,只需证2yA=yM+yB,等式两边同时除以xM,则有2kOA=kOM+kON.
因为kOM+kON=y1x1+y2x2=y1x2+y2x1x1x2
=kx1+12x2+kx2+12x1x1x2
=2kx1x2+12(x1+x2)x1x2=2k+14k2+12×1-kk214k2=2.
又kOA=kOP=1,所以等式成立,即A为线段BM的中点.
8.(2015年四川卷)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( ).
A.(1,3) B.(1,4) C.(2,3) D.(2,4)
【解析】如图,设A(x1,y1),B(x2,y2),M(x0,y0),
则y12=4x1,y22=4x2,两式相减,得(y1+y2)(y1-y2)=4(x1-x2).
当l的斜率k不存在时,符合条件的直线l必有两条.
当k存在时,x1≠x2,则有y1+y22·y1-y2x1-x2=2,
又y1+y2=2y0,所以y0k=2.
由CM⊥AB,得k·y0-0x0-5=-1,即y0k=5-x0,因此2=5-x0,x0=3,
即点M必在直线x=3上.
将点x=3代入y2=4x,得y2=12,则有-23
又y02+4>4(为保证有4条,当k存在时,y0≠0),
所以4
9.(2017岳阳二模)直线3x-4y+4=0与抛物线x2=4y、圆x2+(y-1)2=1从左至右的交点依次为A,B,C,D,则|CD||AB|的值为 .
【解析】如图,抛物线x2=4y的焦点为F(0,1),直线3x-4y+4=0过点(0,1).设A(x1,y1),D(x2,y2),由x2=4y,3x-4y+4=0,得4y2-17y+4=0,解得y1=14,y2=4.∴A(-1,14),D(4,4),
∴|AF|=54,|DF|=5,
∴|CD||AB|=|DF|-1|AF|-1=5-154-1=16.
【答案】16
10.(2017湖南联考)已知点N(1,2),过点N的直线交双曲线x2-y22=1于A,B两点,且ON=12(OA+OB),则直线AB的方程为 .
【解析】由题意知直线AB的斜率存在,设A(x1,y1),B(x2,y2).∵ON=12(OA+OB),∴N是AB的中点,∴x1+x2=2,y1+y2=4.∵x12-y122=1,x22-y222=1,两式相减,得y1-y2x1-x2=2(x1+x2)y1+y2=1.
∴直线AB的方程为y-2=x-1,即x-y+1=0.
【答案】x-y+1=0
11.(2017咸阳市模拟)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,离心率为12,点A在椭圆C上,AF1=2,∠F1AF2=60°,过点F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为P,Q的中点.
(1)求椭圆C的方程;
(2)已知点M0,18,且MN⊥PQ,求直线MN所在的直线方程.
【解析】(1)由e=12,得a=2c,因为AF1=2,AF2=2a-2,
由余弦定理得AF1|2+AF2 2-2AF1·AF2cos A=
|F1F2|2,
解得c=1,a=2,所以b2=a2-c2=3.
所以椭圆C的方程为x24+y23=1.
(2)因为直线PQ的斜率存在,设直线PQ的方程为y=k(x-1),P(x1,y1),Q(x2,y2),
联立y=k(x-1),x24+y23=1,得(3+4k2)x2-8k2x+4k2-12=0.
则x1+x2=8k23+4k2,
y1+y2=k(x1+x2)-2k=-6k3+4k2.
此时N4k23+4k2,-3k3+4k2,又M0,18,
则kMN=18+3k3+4k20-4k23+4k2=-24k+3+4k232k2.
因为MN⊥PQ,所以kMN=-1k,得k=12或k=32.
则kMN=-2或kMN=-23.
所以直线MN的方程为16x+8y-1=0或16x+24y-3=0.
12.(2017青岛市质检)已知椭圆Γ:x2a2+y2=1(a>1)的左焦点为F1,右顶点为A1,上顶点为B1,过F1,A1,B1三点的圆P的圆心坐标为3-22,1-62.
(1)求椭圆的方程;
(2)若直线l:y=kx+m(k,m为常数,k≠0)与椭圆Γ交于不同的两点M和N.
①当直线l过点E(1,0),且EM+2EN=0时,求直线l的方程;
②当坐标原点O到直线l的距离为32,且△MON的面积为32时,求直线l的倾斜角.
【解析】(1)∵A1(a,0),B1(0,1),∴A1B1的中点为a2,12,A1B1的斜率为-1a,
∴A1B1的垂直平分线方程为y-12=ax-a2.
∵圆P过点F1,A1,B1三点,∴圆心P在A1B1的垂直平分线上.
∴1-62-12=a3-22-a2,解得a=3或a=-2(舍去).
∴椭圆的方程为x23+y2=1.
(2)设M(x1,y1),N(x2,y2),
由x23+y2=1,y=kx+m,可得(3k2+1)y2-2my+m2-3k2=0,
∴y1+y2=2m3k2+1,y1y2=m2-3k23k2+1. ③
①∵直线l过点E(1,0),∴k+m=0. ④
∵EM+2EN=0,∴(x1-1,y1)+2(x2-1,y2)=(0,0).
∴y1+2y2=0. ⑤
由③④⑤可得,k=1,m=-1或k=-1,m=1.
∴直线l的方程为y=x-1或y=-x+1.
②∵坐标原点O到直线l的距离为32,
∴|m|k2+1=32⇒m2=34(k2+1). ⑥
结合③得|MN|=1+1k2|y2-y1|
=1+1k2×(y1+y2)2-4y1y2
=1+1k2×2m3k2+12-4×m2-3k23k2+1, ⑦
由⑥⑦得|MN|=3(k2+1)(9k2+1)(3k2+1)2,
∴S△MON=12|MN|×32=343(k2+1)(9k2+1)(3k2+1)2.
∵△MON的面积为32,
∴343(k2+1)(9k2+1)(3k2+1)2=32,解得k=±33.
设直线l的倾斜角为θ,则tan θ=±33,
∵0≤θ<π,∴θ=π6或θ=5π6.
§17.2 直线与椭圆的综合应用
一
椭圆的焦点弦
1.a+c与a-c分别为椭圆上点到焦点距离的最大值和最小值.
2.椭圆的通径(过焦点垂直于长轴的弦)长2b2a,是过椭圆焦点的直线被椭圆所截得的弦长的最小值.
二
直线与椭圆的位置关系的研究方法
1.弦长问题,应用弦长公式及韦达定理,设而不求;有关焦点弦长问题,要重视圆锥曲线的定义的运用,以简化运算.
2.中点弦问题,除了利用韦达定理外,要注意灵活运用“点差法”,设而不求,简化运算.
3.定值问题,常把变动的元素用参数表示出来,然后证明计算结果与参数无关.也可先在特殊条件下求出定值,再给出一般的证明.
4.定点问题,常把方程中参数的同次项集在一起,并令各项的系数为零,求出定点.也可先取参数的特殊值探求定点,然后给出证明.
5.范围(最值)问题:
(1)利用判别式构造不等关系,确定参数的取值范围(最值);
(2)利用隐含或已知的不等关系建立不等式,求出参数的取值范围(最值);
(3)利用基本不等式,求出参数的取值范围(最值);
(4)利用函数的值域,确定目标变量的取值范围(最值);
(5)利用几何图形中的边角大小关系,确定参数的取值范围(最值).
☞左学右考
1 已知经过点(0,2)且斜率为k的直线l与椭圆x22+y2=1有两个不同的交点P和Q,则k的取值范围是( ).
A.-22,22 B.-∞,-22∪22,+∞
C.(-2,2) D.(-∞,-2)∪(2,+∞)
2 已知两定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+3上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( ).
A.55 B.105
C.255 D.2105
3 若点O和点F分别为椭圆x29+y28=1的中心点和左焦点,点P为椭圆上的任意一点,则OP·FP的最小值为 .
4 已知椭圆C的方程为x24+y23=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点.若点D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为 .
基础训练
1.【解析】由题意得,直线l的方程为y=kx+2,代入椭圆方程并整理,得12+k2x2+22kx+1=0.直线l与椭圆有两个不同的交点P和Q等价于Δ=8k2-412+k2=4k2-2>0,解得k<-22或k>22,即k的取值范围为-∞,-22∪22,+∞.故选B.
【答案】B
2.【解析】点A(-1,0)关于直线l的对称点为A'(-3,2),连接A'B交直线l于点P,则椭圆C的长轴长的最小值为|A'B|=25,所以椭圆C的离心率的最大值为ca=15=55,故选A.
【答案】A
3.【解析】设P(x,y)(-3≤x≤3,-22≤y≤22)为椭圆x29+y28=1上的任意一点,依题意得左焦点F(-1,0),∴OP=(x,y),FP=(x+1,y),∴OP·FP=x(x+1)+y2=x2+x+72-8x29=19x+922+234.
∵-3≤x≤3,∴32≤x+92≤152,∴94≤x+922≤2254.
∴14≤19x+922≤254,∴6≤19x+922+234≤12,即6≤OP·FP≤12.故最小值为6.
【答案】6
4.【解析】设点P(x0,y0),M(4,yM),N(4,yN),则直线PA、PB所在的直线方程分别为y=y0x0+2(x+2)、y=y0x0-2(x-2),依题意,可求得yM=6y0x0+2,yN=2y0x0-2.∵DM=(-3,yM),DN=(-3,yN),∴DM·DN=9+12y02x02-4.又x024+y023=1,∴12-3x02=4y02,即12y02x02-4=-9,∴DM·DN=0,∴MN为过D、M、N三点的圆的直径.
设定点为E(t,0),则MN为线段DE的垂直平分线,∴7+t2=4,解得t=1,故定点坐标为(1,0).
【答案】(1,0)
题型一
椭圆中的定值问题
【例1】(2015年四川卷)如图,椭圆E:x2a2+y2b2=1(a>b>0)的离心率是22,点P(0,1)在短轴CD上,且PC·PD=-1.
(1)求椭圆E的方程.
(2)设O为坐标原点,过点P的动直线与椭圆交于A,B两点.是否存在常数λ,使得OA·OB+λPA·PB为定值?若存在,求λ的值;若不存在,请说明理由.
【解析】(1)由题意得,点C,D的坐标分别为(0,-b),(0,b),
又点P的坐标为(0,1),且PC·PD=-1,
所以1-b2=-1,ca=22,a2-b2=c2,解得a=2,b=2,
所以椭圆E的方程为x24+y22=1.
(2)当直线AB的斜率存在时,设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2),
联立x24+y22=1,y=kx+1,得(2k2+1)x2+4kx-2=0.
其判别式Δ=(4k)2+8(2k2+1)>0,
所以x1+x2=-4k2k2+1,x1x2=-22k2+1.
从而OA·OB+λPA·PB=x1x2+y1y2+λ[x1x2+(y1-1)(y2-1)]
=(1+λ)(1+k2)x1x2+k(x1+x2)+1
=(-2λ-4)k2+(-2λ-1)2k2+1=-λ-12k2+1-λ-2,
所以当λ=1时,-λ-12k2+1-λ-2=-3,
此时OA·OB+λPA·PB=-3为定值.
当直线AB的斜率不存在时,直线AB即为直线CD,
此时OA·OB+λPA·PB=OC·OD+λPC·PD=-2-λ,当λ=1时,也满足OA·OB+λPA·PB=-3.
故存在常数λ=1,使得OA·OB+λPA·PB为定值-3.
(1)定值问题,涉及面较多,解决此类问题以坐标运算为主,需建立相应的目标函数,然后代入相应的坐标运算结果即可.
(2)定点问题,可先用特殊值法求出,然后再验证,这样可确定代数式的整理方向和目标.
(3)“值的存在”问题,结论有两种:如果存在,找出一个来;如果不存在,需说明理由.这类问题常用“肯定顺推”.
【变式训练1】(2016年北京卷)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为32,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:|AN|·|BM|为定值.
【解析】(1)由题意得ca=32,12ab=1,a2=b2+c2,解得a=2,b=1,
所以椭圆C的方程为x24+y2=1.
(2)由(1)知,A(2,0),B(0,1).
设P(x0,y0),则x02+4y02=4.
当x0≠0时,直线PA的方程为y=y0x0-2(x-2).
令x=0,得yM=-2y0x0-2,从而|BM|=|1-yM|=1+2y0x0-2.
直线PB的方程为y=y0-1x0x+1.
令y=0,得xN=-x0y0-1,从而|AN|=|2-xN|=2+x0y0-1.
所以|AN|·|BM|=2+x0y0-1·1+2y0x0-2
=x02+4y02+4x0y0-4x0-8y0+4x0y0-x0-2y0+2
=4x0y0-4x0-8y0+8x0y0-x0-2y0+2=4.
当x0=0时,y0=-1,|BM|=2,|AN|=2,
所以|AN|·|BM|=4.
综上所述,|AN|·|BM|为定值.
题型二
椭圆中的定点问题
【例2】(2017河南洛阳模拟)设M是焦距为2的椭圆E:
x2a2+y2b2=1(a>b>0)上一点,A,B是椭圆E的左、右顶点,直线MA,MB的斜率分别为k1,k2,且k1k2=-12.
(1)求椭圆E的方程;
(2)已知椭圆E:x2a2+y2b2=1(a>b>0)上点N(x0,y0)处的切线方程为x0xa2+y0yb2=1.若点P是直线x=2上任意一点,从点P向椭圆E作切线,切点分别为C,D,求证:直线CD恒过定点,并求出该定点的坐标.
【解析】(1)设A(-a,0),B(a,0),M(m,n),
则m2a2+n2b2=1,即n2=b2·a2-m2a2.
由k1k2=-12,即nm+a·nm-a=-12,
得n2m2-a2=-12,
则a2=2b2.又c2=a2-b2=1,解得a2=2,b2=1.
所以椭圆E的方程为x22+y2=1.
(2)设点P(2,t),切点C(x1,y1),D(x2,y2),
则两条切线PC,PD的方程分别为x1x2+y1y=1,x2x2+y2y=1.
因为点P在切线PC,PD上,所以x1+y1t=1,x2+y2t=1,
故C(x1,y1),D(x2,y2)均满足方程x+ty=1,
即x+ty=1为直线CD的方程.
令y=0,得x=1,故直线CD过定点(1,0).
定点问题多为两类,一是证明直线过定点,应根据已知条件建立直线方程中斜率k或截距b的关系式,此类问题中的定点多在坐标轴上;二是证明圆过定点,此类问题应抓住圆心,利用向量转化相应条件,从而找出相应参数满足的条件,确定定点.
【变式训练2】设椭圆E:x2a2+y21-a2=1的焦点在x轴上.
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1、F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q.证明:当a变化时,点P在某定直线上.
【解析】(1)因为椭圆的焦点在x轴上且焦距为1,所以2a2-1=14,解得a2=58.
故椭圆E的方程为8x25+8y23=1.
(2)设P(x0,y0),F1(-c,0),F2(c,0),其中c=2a2-1.
由题设知x0≠c,则直线F1P的斜率kF1P=y0x0+c,
直线F2P的斜率kF2P=y0x0-c.
故直线F2P的方程为y=y0x0-c(x-c).
当x=0时,y=cy0c-x0,即点Q的坐标为0,cy0c-x0.
因此,直线F1Q的斜率为kF1Q=y0c-x0.
由于F1P⊥F1Q,所以kF1P·kF1Q=y0x0+c·y0c-x0=-1.
化简得y02=x02-(2a2-1). ①
将①代入椭圆E的方程,由于点P(x0,y0)在第一象限,解得x0=a2,y0=1-a2,即点P在定直线x+y=1上.
题型三
椭圆中的范围与最值问题
【例3】(2017河南洛阳统考)已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为22,坐标原点O到过右焦点F且斜率为1的直线的距离为22.
(1)求椭圆的标准方程.
(2)设过右焦点F且与坐标轴不垂直的直线l交椭圆于P,Q两点,在线段OF上是否存在点M(m,0),使得|MP|=|MQ|?若存在,求出m的取值范围;若不存在,请说明理由.
【解析】(1)设椭圆的方程为x2a2+y2b2=1(a>b>0),F(c,0)(c>0),由坐标原点O到直线x-y-c=0的距离为22,得|0-0-c|2=22,解得c=1.
又e=ca=22,∴a=2,b=1.
∴椭圆的标准方程为x22+y2=1.
(2)假设存在点M(m,0)(0
∴设直线l的方程为y=k(x-1)(k≠0),P(x1,y1),Q(x2,y2).
由x2+2y2=2,y=k(x-1),得(1+2k2)x2-4k2x+2k2-2=0.
∵Δ>0恒成立,∴x1+x2=4k21+2k2,x1x2=2k2-21+2k2.
设线段PQ的中点为N(x0,y0),
则x0=x1+x22=2k21+2k2,y0=k(x0-1)=-k1+2k2.
∵|MP|=|MQ|,∴MN⊥PQ,∴kMN·kPQ=-1,
即-k1+2k22k21+2k2-m·k=-1,∴m=k21+2k2=12+1k2.
∵k2>0,∴0
圆锥曲线中最值问题的解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.
【变式训练3】(2013年全国Ⅱ卷)平面直角坐标系xOy中,过椭圆M:x2a2+y2b2=1(a>b>0)右焦点的直线x+y-3=0交M于A,B两点,P为AB的中点,且OP的斜率为12.
(1)求M的方程;
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
【解析】(1)设A(x1,y1),B(x2,y2),则x12a2+y12b2=1,x22a2+y22b2=1,
两式相减,得(x1-x2)(x1+x2)a2+(y1-y2)(y1+y2)b2=0.
因为y1-y2x1-x2=-1,设P(x0,y0),又P为AB的中点,且OP的斜率为12,
所以y0=12x0,即y1+y2=12(x1+x2),解得a2=2b2,
即a2=2(a2-c2),即a2=2c2.又因为c=3,所以a2=6.
所以M的方程为x26+y23=1.
(2)因为CD⊥AB,直线AB的方程为x+y-3=0,设直线CD的方程为y=x+m,
将x+y-3=0代入x26+y23=1,得2x2-43x=0,解得x=0或x=433.
不妨令A(0,3),B433,-33,可得|AB|=463.
将y=x+m代入x26+y23=1,得3x2+4mx+2m2-6=0,
设C(x3,y3),D(x4,y4),
则|CD|=2·(x3+x4)2-4x3x4=22318-2m2.
又因为Δ=16m2-12(2m2-6)>0,即-2
方法
椭圆中的弦长计算
1.有关弦的三个问题
涉及弦长的问题,应熟练地利用根与系数的关系,设而不求计算弦长;涉及垂直关系往往也是利用根与系数的关系设而不求简化运算;涉及过焦点的弦的问题,可考虑利用圆锥曲线的定义求解.
2.求解与弦有关问题的两种方法
(1)方程组法:联立直线方程和圆锥曲线方程,消元(x或y)成为一元二次方程之后,结合根与系数的关系,建立等式关系或不等式关系.
(2)点差法:在求解圆锥曲线且题目中已有直线与圆锥曲线相交和被截线段的中点坐标时,设出直线和圆锥曲线的两个交点坐标,代入圆锥曲线的方程并作差,从而求出直线的斜率,然后利用中点求出直线方程.“点差法”的常见题型有:求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直平分线问题.必须提醒的是“点差法”具有不等价性,即要考虑判别式Δ是否为正数.
【突破训练】(2017衡水中学三模)如图,已知P62,1为椭圆E:x2a2+y2b2=1(a>b>0)上的点,且a2+b2=5,过点P的动直线与圆F:x2+y2=a2+1相交于A、B两点,过点P作直线AB的垂线与椭圆E相交于点Q.
(1)求椭圆E的离心率;
(2)若AB=23,求|PQ|.
【解析】(1)依题知64a2+1b2=1,a2+b2=5,a>b>0,
解得a2=3,b2=2,
所以椭圆E的离心率e=a2-b2a2=33.
(2)依题知圆F的圆心为原点,半径r=2,|AB|=23,
所以原点到直线AB的距离d=r2-AB2222-2322=1.因为点P的坐标为62,1,所以直线AB的斜率存在,设为k.
所以直线AB的方程为y-1=kx-62,
即kx-y-62k+1=0,
所以d=1-62k1+k2=1,解得k=0或k=26.
当k=0时,直线PQ的方程为x=62,
所以|PQ|的值为点P纵坐标的两倍,即|PQ|=2×1=2.
当k=26时,直线PQ的方程为y-1=-126x-62,代入椭圆E的方程x23+y22=1,消去y并整理,得34x2-106x-21=0.
设点Q的坐标为(x1,y1),所以62+x1=10634,解得x1=-7634,
所以|PQ|=1+-1262x1-62=3017.
(1)由待定系数法求出a,b,c,再根据离心率的定义求椭圆E的离心率.
(2)先根据垂径定理求圆心到直线AB的距离,再根据点到直线的距离公式求直线AB的斜率,然后根据垂直关系求直线PQ的斜率,最后联立直线PQ与椭圆方程,利用韦达定理及弦长公式求|PQ|.
1.(2017天水一模)过抛物线C:x2=2y的焦点F的直线l交抛物线C于A、B两点,若抛物线C在点B处的切线斜率为1,则线段|AF|=( ).
A.1 B.2 C.3 D.4
【解析】∵x2=2y,∴y'=x.∵抛物线C在点B处的切线斜率为1,∴B1,12.∵x2=2y的焦点为F0,12,∴直线l的方程为y=12,∴|AF|=1,故选A.
【答案】A
2.(2017太原模拟)已知点F1、F2是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,若双曲线左支上存在点P与点F2关于直线y=bax对称,则该双曲线的离心率为( ).
A.2 B.52 C.2 D.5
【解析】如图所示,点P与点F2关于直线y=bax对称,
∴OP=OF2=OF1=c,
∴PF1⊥PF2.又∵tan∠PF1F2=ba,F1F2=2c,∴PF2=2b,PF1=2a.
∵点P在双曲线上,
∴PF2-PF1=2a⇒2b-2a=2a⇒b=2a⇒e=ca=5.
【答案】D
3.(2017长沙月考)已知椭圆C:x29+y2m=1(0
4.(2017四川绵阳模考)已知椭圆x216+y24=1的左顶点为A,过点A作两条弦AM、AN分别交椭圆于M、N两点,直线AM、AN的斜率记为k1,k2,且满足k1·k2=-2,则直线MN经过的定点为 .
【解析】由x216+y24=1,y=k1(x+4),得xM=4-16k121+4k12.
同理xN=4-16k221+4k22=4k12-64k12+16.
所以yM=8k11+4k12,yN=-16k116+k12,取k1=1,可得直线MN的方程为9x-4y+28=0,
由对称性可知,直线MN经过x轴上的定点-289,0.
【答案】-289,0
5.(2017湖南六校联考)设椭圆C1:x2a2+y2b2=1(a>b>0)的离心率为32,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是4+23.
(1)求椭圆C1的方程;
(2)设椭圆C1的左、右顶点分别为A、B,过椭圆C1上的一点D作x轴的垂线交x轴于点E,若点C满足AB⊥BC,AD∥OC,连接AC交DE于点P,求证:PD=PE.
【解析】(1)由e=32,知ca=32,所以c=32a.
因为△PF1F2的周长是4+23,
所以2a+2c=4+23,所以a=2,c=3,
所以b2=a2-c2=1,
所以椭圆C1的方程为x24+y2=1.
(2)由(1)得A(-2,0),B(2,0),
设D(x0,y0),所以E(x0,0).
因为AB⊥BC,设C(2,y1),
所以AD=(x0+2,y0),OC=(2,y1).
由AD∥OC,得(x0+2)y1=2y0,即y1=2y0x0+2,
所以直线AC的方程为y2y0x0+2=x+24,
整理得y=y02(x0+2)(x+2).
又点P在直线DE上,将x=x0代入直线AC的方程,可得y=y02,即点P的坐标为x0,y02,
所以P为DE的中点,所以PD=PE.
6.(2017汉中市质检)已知直线l:y=kx+3与y轴的交点是椭圆C:x2+y2m=1(m>0)的一个焦点.
(1)求椭圆C的方程.
(2)若直线l与椭圆C交于A、B两点,是否存在k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
【解析】(1)因为直线l:y=kx+3与y轴的交点坐标为F(0,3),
所以椭圆C:x2+y2m=1(m>0)的一个焦点坐标为F(0,3),
所以椭圆的焦半距c=3,所以m=c2+1=3+1=4,
故椭圆C的方程为y24+x2=1.
(2)将直线l的方程y=kx+3代入y24+x2=1并整理,得(k2+4)x2+23kx-1=0.
设点A(x1,y1),B(x2,y2),则x1+x2=-23kk2+4,x1x2=-1k2+4.
假设以线段AB为直径的圆恰好经过坐标原点O,
则OA·OB=0,即x1x2+y1y2=0.
又y1y2=k2x1x2+3k(x1+x2)+3,
所以-1+k2k2+4-6k2k2+4+3=0,解得k=±112.
经检验知,此时Δ>0,符合题意.
故存在k=±112,使得以线段AB为直径的圆恰好经过坐标原点O.
7.(2017太原五中二模)已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),点A22,32在椭圆C上.
(1)求椭圆C的标准方程.
(2)是否存在斜率为2的直线l,使得当直线l与椭圆C有两个不同交点M,N时,能在直线y=53上找到一点P,在椭圆C上找到一点Q,满足PM=NQ?若存在,求出直线l的方程;若不存在,请说明理由.
【解析】(1)由题意得椭圆C的半焦距c=1,
∴椭圆C的标准方程为x2a2+y2a2-1=1(a2>1).
∵点A22,32在椭圆上,
∴12a2+34(a2-1)=1(a2>1),解得a2=2.
故椭圆C的标准方程为x22+y2=1.
(2)假设存在这样的直线,设直线l的方程为y=2x+t,点M(x1,y1),N(x2,y2),Px3,53,Q(x4,y4),MN的中点为D(x0,y0),
由y=2x+t,x22+y2=1,得9x2+8tx+2t2-2=0,
∴x1+x2=-8t9,且Δ=(8t)2-36(2t2-2)>0,
则-3
由PM=NQ知,四边形PMQN为平行四边形,
而D为线段MN的中点,因此,D也是线段PQ的中点,
∴y0=53+y42=t9,可得y4=2t-159.
又∵-3
8.(2017福州模拟)已知点A(-4,0),直线l:x=-1与x轴交于点B,动点M到A,B两点的距离之比为2.
(1)求点M的轨迹C的方程;
(2)设C与x轴交于E,F两点,P是直线l上一点,且点P不在C上,直线PE,PF分别与C交于另一点S,T,证明:A,S,T三点共线.
【解析】(1)设点M(x,y),依题意,|MA||MB|=(x+4)2+y2(x+1)2+y2=2,
化简得x2+y2=4,即轨迹C的方程为x2+y2=4.
(2)由(1)知曲线C的方程为x2+y2=4,
令y=0,得x=±2,不妨设E(-2,0),F(2,0),如图.
设P(-1,y0),S(x1,y1),T(x2,y2),则直线PE的方程为y=y0(x+2).
由y=y0(x+2),x2+y2=4,得(y02+1)x2+4y02x+4y02-4=0,
所以-2x1=4y02-4y02+1,即x1=2-2y02y02+1,y1=4y0y02+1.
直线PF的方程为y=-y03(x-2).
由y=-y03(x-2),x2+y2=4,得(y02+9)x2-4y02x+4y02-36=0,
所以2x2=4y02-36y02+9,即x2=2y02-18y02+9,y2=12y0y02+9.
所以kAS=y1x1+4=4y0y02+12-2y02y02+1+4=2y0y02+3,
kAT=y2x2+4=12y0y02+92y02-18y02+9+4=2y0y02+3,
所以kAS=kAT,所以A,S,T三点共线.
9.(2017成都七中模拟)已知椭圆C:x2a2+y2b2=1(a>b>0)的右焦点为(3,0),且经过点-1,32,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方).
(1)求椭圆C的方程;
(2)若|AM|=2|MB|,且直线l与圆O:x2+y2=47相切于点N,求|MN|的长.
【解析】(1)由题意知c=3,且(-1)2b2+3+322b2=1,
解得b2=1,所以a2=4,
所以椭圆C的方程为x24+y2=1.
(2)设M(m,0),直线l:x=ty+m,A(x1,y1),B(x2,y2),
由|AM|=2|MB|,得y1=-2y2.
由x24+y2=1,x=ty+m得(t2+4)y2+2mty+m2-4=0.
则y1+y2=-2tmt2+4,y1y2=m2-4t2+4,
由y1y2=-2y22,y1+y2=-2y2+y2=-y2,
得y1y2=-2-(y1+y2)2=-2(y1+y2)2.
即m2-4t2+4=-2-2tmt2+42,化简得(m2-4)(t2+4)=-8t2m2.
因为原点O到直线l的距离d=|m|1+t2,又直线l与圆O:x2+y2=47相切,
所以|m|1+t2=47,即t2=74m2-1.
联立方程(m2-4)(t2+4)=-8t2m2,t2=74m2-1,得21m4-16m2-16=0,即(3m2-4)(7m2+4)=0,
解得m2=43,此时t2=43,满足Δ>0,此时M233,0或-233,0,
在Rt△OMN中,|MN|=43-47=42121,所以|MN|的长为42121.
10.(2017佛山质检)已知椭圆C1:x2a2+y2b2=1(a>b>0)的焦距为4,左、右焦点分别为F1、F2,且C1与抛物线C2:y2=x的交点所在的直线经过F2.
(1)求椭圆C1的方程;
(2)分别过点F1、F2作平行直线m、n,若直线m与C1交于A,B两点,与抛物线C2无公共点,直线n与C1交于C,D两点,其中点A,D在x轴上方,求四边形AF1F2D的面积的取值范围.
【解析】(1)依题意得2c=4,则左、右焦点分别为F(-2,0)、F2(2,0).
所以椭圆C1与抛物线C2的一个交点为P(2,2),
于是2a=|PF1|+|PF2|=42,从而a=22.
又a2=b2+c2,解得b=2,
所以椭圆C1的方程为x28+y24=1.
(2)依题意,直线m的斜率不为0,设直线m:x=ty-2,
由x=ty-2,y2=x,消去x并整理,得y2-ty+2=0,
由Δ=(-t)2-8<0,得t2<8.
由x=ty-2,x2+2y2=8,消去x并整理,得(t2+2)y2-4ty-4=0.
设A(x1,y1),B(x2,y2),
则y1+y2=4tt2+2,y1y2=-4t2+2,
所以|AB|=1+t2|y1-y2|
=1+t2(y1+y2)2-4y1y2=42(t2+1)t2+2.
因为直线m与n之间的距离d=4t2+1(即点F2到m的距离),
由椭圆的对称性知,四边形ABCD为平行四边形,
故S四边形AF1F2D=12S四边形ABCD=12·42(t2+1)t2+2·4t2+1=82t2+1t2+2.
令t2+1=s∈[1,3),则S四边形AF1F2D=82t2+1t2+2=82ss2+1=82s+1s∈1225,42,
所以四边形AF1F2D的面积的取值范围为1225,42.
§17.3 直线与抛物线的综合应用
直线与抛物线的综合问题的解题策略
在解决直线与抛物线位置关系的问题时,其方法类似于直线与椭圆的位置关系.在解决此类问题时,要熟记抛物线的定义,会根据题中的条件用待定系数法、定义法等方法求抛物线的标准方程,会根据条件研究抛物线的几何性质,会用设而不求思想处理直线与抛物线的位置关系,注意题中向量条件的转化与向量方法的应用.除考虑代数法外,还应借助平面几何的知识,利用数形结合的思想求解.具体解法如下:
1.设直线与方程
(1)设直线时分斜率存在与不存在.
(2)设为y=kx+b或x=my+n(注意两者的弦长公式不同).
2.设交点坐标(设而不求)
3.联立方程组
4.消元韦达定理
与抛物线联立时,经常是把抛物线方程代入直线方程反而更简单.
5.根据条件转化
转化的常见类型:
(1)“以弦AB为直径的圆过点O”(需讨论k是否存在)⇔OA⊥OB⇔k1·k2=-1⇔OA·OB=0⇔x1x2+y1y2=0.
(2)“点在圆内、圆上、圆外问题”⇔“直角、锐角、钝角问题”⇔“向量的数量积大于、等于、小于0问题”⇔x1x2+y1y2大于、等于、小于0.
(3)“等角、角平分、角互补问题”⇔斜率关系(k1+k2=0或k1=k2).
(4)“共线问题”⇔AO=λOB⇔坐标表示⇔A,O,B三点共线⇔直线OA与OB斜率相等.
(5)“点、线对称问题”⇔坐标与斜率关系.
(6)“弦长、面积问题”⇔坐标与弦长公式问题(注意两个面积公式的合理选择).
6.化简与计算
7.细节问题不忽略
(1)判别式是否已经考虑;(2)二次项系数是否会出现0.
☞左学右考
1 过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P,Q两点,若线段PF、FQ的长分别是p、q,则1p+1q等于( ).
A.2a B.12a
C.4a D.4a
2 已知过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点,则|AF||BF|的值为( ).
A.5 B.4
C.3 D.2
3 过抛物线y2=8x上的任意一点为圆心作与直线x+2=0相切的圆,这些圆必过一定点,则该定点坐标是 .
4 过抛物线y2=4x(p>0)的焦点作两条互相垂直的弦AB、CD,求1AB+1CD的值.
基础训练
1.【解析】取直线与x轴垂直的特殊情况,由直线y=14a,得p=q=12a,∴1p+1q=4a.
【答案】C
2.【解析】由题意设直线l的方程为y=3x-p2,即x=y3+p2,代入抛物线方程y2=2px,整理得3y2-2py-3p2=0.设A(xA,yA),B(xB,yB),则yA=3p,yB=-33p,所以|AF||BF|=yAyB=3.
【答案】C
3.【解析】抛物线的焦点为F(2,0),准线l的方程为x=-2,即x+2=0,又抛物线上任意一点到F与到准线l的距离相等,所以这些圆一定过焦点F(2,0).
【答案】(2,0)
4.【解析】由题意得抛物线的焦点坐标为(1,0),设直线AB的方程为y=k(x-1),直线CD的方程为y=-1k(x-1),代入y2=4x,得k2x2-(2k2+4)x+k2=0,则xA+xB=2+4k2,所以AB=xA+xB+2=4+4k2.同理CD=xC+xD=4+4k2.所以1AB+1CD=k24k2+4+14k2+4=14.
题型一
抛物线中的定点定值问题
【例1】(2017辽宁省实验中学模拟)已知抛物线的方程为C:x2=4y,过点Q(0,2)的一条直线与抛物线C交于A,B两点,若抛物线在A,B两点处的切线交于点P.
(1)求点P的轨迹方程.
(2)设直线PQ的斜率存在,为kPQ,直线AB的斜率为kAB,请验证kPQ·kAB是否为定值?若是,计算出该值;若不是,请说明理由.
【解析】(1)由直线AB与抛物线交于两点可知,直线AB不与x轴垂直,
故可设lAB:y=kx+2,代入x2=4y,整理得x2-4kx-8=0, ①
Δ=16k2+32>0,故k∈R时均满足题目要求.
记交点坐标为Ax1,x124,Bx2,x224,则x1,x2为方程①的两个根,故由韦达定理可知,x1+x2=4k,x1x2=-8.
将抛物线方程转化为y=14x2,则y'=12x,
故点A处的切线方程为y-x124=x12(x-x1),整理得y=x12x-x124.同理可得,点B处的切线方程为y=x22x-x224.记两条切线的交点P(xP,yP),
联立两条切线的方程,解得xP=x1+x22=2k,yP=kx1-x124=kx1-(kx1+2)=-2,
故点P的轨迹方程为y=-2,x∈R.
(2)当k=0时,xp=0,yP=-2,此时直线PQ即为y轴,与直线AB的夹角为π2.
当k≠0时,记直线PQ的斜率kPQ=-2-22k-0=-2k,又直线AB的斜率为k,
故kPQ·kAB=-2k·k=-2为定值.
(1)利用导数求抛物线的切线,可避免判别式运算,简化计算过程.
(2)对直线与圆锥曲线的位置关系问题,常用“设而不求”思想,即设出直线方程代入圆锥曲线方程化为关于x的一元二次方程,设出交点坐标,利用根与系数关系,将交点的横坐标之和与积用一元二次方程的系数表示出来,然后根据题中的条件和所求结论,选择合适的方法进行计算,注意题中条件的合理转化.
【变式训练1】(2016河南八市二模)已知F是抛物线C:y2=2px(p>0)的焦点,圆M过坐标原点和点F,且圆心M到抛物线C的准线的距离为32.
(1)求抛物线C的方程.
(2)已知抛物线C上的点N(s,4),过点N作抛物线C的两条互相垂直的弦NA和NB,判断直线AB是否过定点?并说明理由.
【解析】(1)抛物线的焦点为Fp2,0,准线方程为x=-p2.
∵圆M过坐标原点和点F,∴M在直线x=p4上,
∴点M到抛物线的准线的距离d=p2+p4=32,解得p=2.
∴抛物线C的方程为y2=4x.
(2)把y=4代入抛物线方程,得x=4,即N(4,4).
设Ay124,y1,By224,y2,则
kNA=y1-4y12-164=4y1+4,kNB=y22-4y22-164=4y2+4.
∵直线NA和直线NB互相垂直,
∴4y1+4·4y2+4=-1,即y1y2=-4(y1+y2)-32.
设直线AB的方程为x=ty+m,
由x=ty+m,y2=4x,得y2-4ty-4m=0,
∴y1+y2=4t,y1y2=-4m,
∴-4m=-16t-32,即m=4t+8.
∴直线AB的方程为x=ty+4t+8,
当y=-4时,x=8,
∴直线AB过定点(8,-4).
题型二
抛物线中的范围与最值问题
【例2】(2017年浙江卷)如图,已知抛物线x2=y,点A-12,14,B32,94,抛物线上的点P(x,y)-12
(2)求|PA|·|PQ|的最大值.
【解析】(1)设直线AP的斜率为k,则k=x2-14x+12=x-12,
∵-12
kx-y+12k+14=0,x+ky-94k-32=0,
解得点Q的横坐标是xQ=-k2+4k+32(k2+1).
∵|PA|=1+k2x+12=1+k2(k+1),
|PQ|=1+k2(xQ-x)=-(k-1)(k+1)2k2+1,
∴|PA|·|PQ|=-(k-1)(k+1)3.
令f(k)=-(k-1)(k+1)3,∵f'(k)=-(4k-2)(k+1)2,
∴f(k)在区间-1,12上单调递增,在区间12,1上单调递减.
∴当k=12时,|PQ|·|PQ|取得最大值2716.
本题得到的三角形面积是关于m的三次函数,可以用导数法求出面积的最值.一般情况下,若表达式不易转化为基本不等式或者二次函数模型,但易求其导数时,通常可以用导数法求出最值.
【变式训练2】已知直线l:y=kx+1过定点A,动点M(x,y)满足|MA|=|y+1|,动点M的轨迹为C.
(1)求C的方程.
(2)直线l与C交于P,Q两点,以P,Q为切点分别作C的切线,两条切线交于点B.
①求证:AB⊥PQ;
②若直线AB与C交于R,S两点,求四边形PRQS面积的最小值.
【解析】(1)由题意知A(0,1),∵|MA|=|y+1|,
∴x2+(y-1)2=|y+1|,化简得x2=4y.
故C的方程为x2=4y.
(2)①设P(x1,y1),Q(x2,y2),由x2=4y,y=kx+1,消去y,得x2-4kx-4=0,
显然Δ=16k2+16>0,且x1+x2=4k,x1x2=-4.
由x2=4y,得y=14x2,∴y'=12x,
∴以P为切点的切线的斜率为k1=12x1,切线方程为y-y1=12x1(x-x1).
又∵x12=4y1,
∴以P为切点的切线方程为x1x=2(y+y1). ③
同理,以Q为切点的切线方程为x2x=2(y+y2). ④
由④-③且x1≠x2,得点B的横坐标x=x1+x22=2k,
将x=2k代入③中,得y=kx1-y1=-1,∴点B的坐标为(2k,-1).
当k=0时,显然AB⊥PQ.
当k≠0时,kAB=2-2k=-1k.∵kAB·kPQ=-1,∴AB⊥PQ.
②由已知,显然直线l的斜率不为0,由①知AB⊥PQ,∴kAB=-1k,
故直线AB的方程为y=-1kx+1.
设R(x3,y3),S(x4,y4),
由x2=4y,y=-1kx+1,消去y,得x2+4kx-4=0,显然Δ=16k2+16>0,且x3+x4=-4k,x3x4=-4.
易得|PQ|=(x1-x2)2+(y1-y2)2
=(1+k2)(x1-x2)2
=(1+k2)[(x1+x2)2-4x1x2]=4(k2+1),
|RS|=(x3-x4)2+(y3-y4)2
=1+1k2(x3-x4)2
=1+1k2[(x3+x4)2-4x3x4]=41k2+1.
∵AB⊥PQ,∴RS⊥PQ,
∴S四边形PRQS=12|PQ|·|RS|=81k2+1(k2+1)=8k2+1k2+2≥32,
当且仅当k=±1时,四边形PRQS面积取最小值32.
题型三
抛物线中的证明问题
【例3】已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(1)求抛物线C的方程;
(2)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x-1)2+y2=1相切,切点分别为A,B,求证:A,B,F三点共线.
【解析】(1)抛物线C的准线方程为x=-p2,
∴|MF|=m+p2=2.
又∵抛物线C:y2=2px(p>0)过点M(m,2),
∴4=2pm,即4=2p2-p2,
∴p2-4p+4=0,∴p=2,
∴抛物线C的方程为y2=4x.
(2)设点E(0,t)(t≠0),已知切线不为y轴.设直线EA:y=kx+t,联立y=kx+t,y2=4x,消去y,可得k2x2+(2kt-4)x+t2=0.
∵直线EA与抛物线C相切,
∴Δ=(2kt-4)2-4k2t2=0,即kt=1,
代入k2x2+(2kt-4)x+t2=0,得1t2x2-2x+t2=0,∴x=t2,即A(t2,2t).
设切点B(x0,y0),则点O,B关于直线EF:y=-tx+t对称,
则y0x0×t-00-1=-1,y02=-t·x02+t,解得x0=2t2t2+1,y0=2tt2+1,
即B2t2t2+1,2tt2+1.
当t≠±1时,直线AF的斜率kAF=2tt2-1,
直线BF的斜率kBF=2tt2+1-02t2t2+1-1=2tt2-1,∴kAF=kBF,即A,B,F三点共线.
当t=±1时,A(1,±2),B(1,±1),此时A,B,F三点共线.
综上可知,A,B,F三点共线.
解析几何中共线问题的处理方法:
(1)求出两点所在的直线方程,再证明第三点在所求出的直线上;
(2)证明两点连线的斜率相等;
(3)用向量法解决共线问题.
【变式训练3】(2017长春质检一)以边长为4的等边三角形ABC的顶点A以及BC边的中点D为左、右焦点的椭圆过B,C两点.
(1)求该椭圆的标准方程;
(2)过点D且与x轴不垂直的直线l交椭圆于M,N两点,求证:直线BM与CN的交点在一条直线上.
【解析】(1)由题意可知两个焦点为(-3,0)与(3,0),且2a=6,因此椭圆的标准方程为x29+y26=1.
(2)当MN不与x轴重合时,设MN的方程为x=my+3,且B(3,),C(3,-2),
联立2x2+3y2-18=0,x=my+3,消去x,得(2m2+3)y2+43my-12=0,即y1+y2=-43m2m2+3,y1y2=-122m2+3.设M(x1,y1),N(x2,y2),
则直线BM:y-2=y1-2x1-3(x-3), ①
直线CN:y+2=y2+2x2-3(x-3). ②
由②-①得4=(x-3)y2+2x2-3-y1-2x1-3=(x-3)·my1(y2+2)-my2(y1-2)m2y1y2=(x-3)2y1+2y2my1y2=(x-3)·-83m2m2+3-12m2m2+3=233(x-3),
则x-3=23,即x=33.
当MN与x轴重合时,即MN的方程为x=0,即M(3,0),N(-3,0).
则直线BM:y-2=-23-3(x-3), ③
直线CN:y+2=2-3-3(x-3). ④
联立③④消去y,得x=33.
综上可知,直线BM与CN的交点在直线x=33上.
方法
抛物线中的存在性问题求解
解决图形的存在性问题,先假设存在,推证满足条件的结论,若结论正确,则存在;若结论不正确,则不存在.注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件.
【突破训练】(2014年山东卷)已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|.当点A的横坐标为3时,△ADF为正三角形.
(1)求C的方程.
(2)若直线l1∥l,且l1和C有且只有一个公共点E,
①证明直线AE过定点,并求出定点坐标.
②△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
【解析】(1)由题意知Fp2,0.
设D(t,0)(t>0),则FD的中点为p+2t4,0.
因为|FA|=|FD|,
由抛物线的定义知3+p2=t-p2,
解得t=3+p或t=-3(舍去).
由p+2t4=3,解得p=2.
所以抛物线C的方程为y2=4x.
(2)①由(1)知F(1,0).
设A(x0,y0)(x0y0≠0),D(xD,0)(xD>0).
因为|FA|=|FD|,则|xD-1|=x0+1,
由xD>0得xD=x0+2,故D(x0+2,0),
故直线AB的斜率kAB=-y02.
因为直线l1和直线AB平行,
设直线l1的方程为y=-y02x+b,
代入抛物线方程,得y2+8y0y-8by0=0,
由题意Δ=64y02+32by0=0,得b=-2y0.
设E(xE,yE),则yE=-4y0,xE=4y02.
当y02≠4时,kAE=yE-y0xE-x0=-4y0+y04y02-y024=4y0y02-4,
可得直线AE的方程为y-y0=4y0y02-4(x-x0).
由y02=4x0,
整理可得y=4y0y02-4(x-1),
则直线AE恒过点F(1,0).
当y02=4时,直线AE的方程为x=1,也过点F(1,0),
所以直线AE过定点F(1,0).
②由①知直线AE过焦点F(1,0),
所以|AE|=|AF|+|FE|=(x0+1)+1x0+1=x0+1x0+2.
设直线AE的方程为x=my+1.
因为点A(x0,y0)在直线AE上,故m=x0-1y0.
设B(x1,y1).直线AB的方程为y-y0=-y02(x-x0),
由y0≠0,可得x=-2y0y+2+x0,
代入抛物线方程,得y2+8y0y-8-4x0=0,
所以y0+y1=-8y0,
可求得y1=-y0-8y0,x1=4x0+x0+4.
所以点B到直线AE的距离为
d=|4x0+x0+4+my0+8y0-1|1+m2
=4(x0+1)x0=4x0+1x0.
则△ABE的面积
S=12×4x0+1x0x0+1x0+2≥16,
当且仅当1x0=x0,即x0=1时等号成立.
所以△ABE的面积的最小值为16.
1.(2017南昌八校联考)已知坐标原点为O,A、B为抛物线y2=4x上异于点O的两点,且OA·OB=0,则AB的最小值为( ).
A.4 B.8 C.16 D.64
【解析】由于OA·OB=0,故可设直线OA、OB的方程分别为y=kx、y=-1kx,分别与抛物线方程联立,得A4k2,4k,B(4k2,-4k),所以AB=4k2-4k22+4k+4k2=4k4+1k4+k2+1k2≥8.
【答案】B
2.(2017山西质检)直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率分别为k1,k2,且满足k1k2=23,则直线l一定过点( ).
A.(-3,0) B.(3,0)
C.(-1,3) D.(-2,0)
【解析】设直线l的方程为x=my+b,联立直线和抛物线的方程得x=my+b,y2=2x,整理得y2-2my-2b=0.设A(x1,y1),B(x2,y2),由根与系数的关系得y1y2=-2b,y1+y2=2m,故x1x2=(my1+b)(my2+b)=m2y1y2+mb(y1+y2)+b2=-2bm2+2bm2+b2=b2.因为k1k2=y1y2x1x2=-2bb2=23,解得b=-3,故直线l的横截距为定值-3,即直线l一定过点(-3,0).
【答案】A
3.(2017衡水中学押题卷)焦点为F的抛物线C:y2=8x的准线与x轴交于点A,点M在抛物线C上,则当|MA||MF|取得最大值时,直线MA的方程为( ).
A.y=x+2或y=-x-2
B.y=x+2
C.y=2x+2或y=-2x+2
D.y=-2x+2
【解析】过点M作MP与准线垂直,垂足为P(如图),
则|MA||MF|=|MA||MP|=1cos∠AMP=1cos∠MAF,
则当|MA||MF|取得最大值时,∠MAF必须取得最大值.
此时直线AM与抛物线相切,可设切线方程为y=k(x+2),与y2=8x联立,消去x,得ky2-8y+16k=0,所以Δ=64-64k2=0,解得k=±1.
则直线MA的方程为y=x+2或y=-x-2.故选A.
【答案】A
4.(2017河南质检)已知点A(2,0),B(4,0),动点P在抛物线y2=-4x上运动,当AP·BP取得最小值时的点P的坐标为 .
【解析】设P-y24,y,则AP=-y24-2,y,BP=-y24-4,y,所以AP·BP=-y24-2-y24-4+y2=y416+52y2+8≥8,当且仅当y=0时取等号,此时点P的坐标为(0,0).
【答案】(0,0)
5.(2017浙江联考)已知抛物线C:y2=2px(p>0),点F为其焦点,点N(3,1)在抛物线C的内部,设点M是抛物线C上的任意一点,|MF|+|MN|的最小值为4.
(1)求抛物线C的方程.
(2)过点F作直线l与抛物线C交于不同两点A、B,与y轴交于点P,且PF=λ1FA=λ2FB,试判断λ1+λ2是否为定值?若是定值,求出该定值;若不是定值,请说明理由.
【解析】(1)准线方程l:x=-p2,设点M到l的距离为d,
由抛物线定义,有|MF|+|MN|=d+|MN|≥3+p2=4,
∴p=2,∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),F(1,0).
由题意知直线l的斜率k存在且不等于0,
设直线l:y=k(x-1),则P(0,-k),由PF=λ1FA=λ2FB知,(1,k)=λ1(x1-1,y1)=λ2(x2-1,y2),
∴k=λ1y1=λ2y2.∵k≠0,
∴λ1=ky1,λ2=ky2,λ1+λ2=k×y1+y2y1y2.
将y=k(x-1)代入y2=4x,得y2-4ky-4=0,
∴y1+y2=4k,y1y2=-4,
∴y1+y2y1y2=-4k×14=-1k,
∴λ1+λ2=k×-1k=-1为定值.
6.(2017南充高级中学检测)已知抛物线C:x2=2py(p>0),过其焦点作斜率为1的直线l交抛物线C于M、N两点,且|MN|=16.
(1)求抛物线C的方程;
(2)已知动圆P的圆心在抛物线C上,且过定点D(0,4),若动圆P与x轴交于A、B两点,且|DA|<|DB|,求|DA||DB|的最小值.
【解析】(1)设抛物线的焦点为F0,p2,则直线l:y=x+p2.
由y=x+p2,x2=2py,得x2-2px-p2=0,
∴x1+x2=2p,y1+y2=3p,
∴|MN|=y1+y2+p=4p=16,∴p=4,
∴抛物线C的方程为x2=8y.
(2)设动圆圆心P(x0,y0),A(x1,0),B(x2,0),则x02=8y0,且圆P:(x-x0)2+(y-y0)2=x02+(y0-4)2,
令y=0,整理得x2-2x0x+x02-16=0,解得x1=x0-4,x2=x0+4.
∴|DA||DB|=(x0-4)2+16(x0+4)2+16=x02-8x0+32x02+8x0+32
=1-16x0x02+8x0+32,
当x0=0时,|DA||DB|=1.
当x≠0时,|DA||DB|=1-16x0+32x0+8.
∵x0>0,∴x0+32x0≥82,
∴|DA||DB|≥1-168+82=3-22=2-1.
∵2-1<1,∴|DA||DB|的最小值为2-1.
7.(2017南京二模)已知抛物线E:y2=2px(p>0)的焦点为F,过点F且垂直于x轴的直线与抛物线E交于S,T两点,以P(3,0)为圆心的圆过点S,T,且∠SPT=90°.
(1)求抛物线E和圆P的方程;
(2)设M是圆P上的点,过点M且垂直于FM的直线l交E于A,B两点,证明:FA⊥FB.
【解析】(1)将x=p2代入y2=2px,得y=±p,∴|ST|=2p.
又∵∠SPT=90°,∴△SPT是等腰直角三角形.
∴|SF|=|PF|,即p=3-p2,解得p=2,
∴抛物线E的方程为y2=4x.
此时圆P的半径为2p=22,∴圆P的方程为(x-3)2+y2=8.
(2)设M(x0,y0),则(x0-3)2+y02=8,即y02=-x02+6x0-1. ①
设Ay124,y1,By224,y2,则FM=(x0-1,y0),AB=y22-y124,y2-y1,MA=y124-x0,y1-y0,MB=y224-x0,y2-y0.
∵FM⊥AB,MA∥MB,
∴y22-y124(x0-1)+y0(y2-y1)=0,y124-x0(y2-y0)-y224-x0(y1-y0)=0.
∵y1≠y2,∴(y1+y2)(x0-1)+4y0=0,y1y2-y0(y1+y2)+4x0=0.
若x0=1,则y0=0,此时不满足①,故x0-1≠0,
∴y1+y2=4y01-x0,y1y2=20x0-41-x0,
∴FA·FB=y124-1y224-1+y1y2=y12y2216-(y1+y2)24+1+32y1y2=(5x0-1)2(1-x0)2-4y02(1-x0)2+1+30x0-61-x0=24x0-4x02-4-4y02(1-x0)2=-4(x02+y02-6x0+1)(1-x0)2=0,
∴FA⊥FB.
8.(2017成都七中三模)如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:x2a2+y2b2=1(a>b>0)的右焦点F2,F1为C2的左焦点.椭圆C2的离心率为e=12,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q两点之间移动.
(1)当a2+3b取最小值时,求C1和C2的方程;
(2)若△PF1F2的边长恰好是三个连续的自然数,求△MPQ面积的最大值以及此时直线MP的方程.
【解析】(1)因为c=m,e=ca=12,则a=2m,b=3m,所以a2+3b取最小值时m=1,
所以抛物线C1:y2=-4x.此时a=2,b2=3,所以椭圆C2的方程为x24+y23=1.
(2)因为c=m,e=ca=12,则a=2m,b=3m,设椭圆的标准方程为x24m2+y23m2=1,点P(x0,y0),Q(x1,y1),
由x24m2+y23m2=1,y2=-4mx,得3x2-16mx-12m2=0,
所以x0=-23m或x0=6m(舍去).代入抛物线方程得y0=263m,即P-2m3,26m3,
所以|PF1|=5m3,|PF2|=2a-|PF1|=7m3,|F1F2|=2m=6m3.
又△PF1F2的边长恰好是三个连续的自然数,所以m=3.
此时抛物线的方程为y2=-12x,F1(-3,0),P(-2,26),
则直线PQ的方程为y=26(x+3).
联立y=26(x+3),y2=-12x,得x1=-92或x1=-2(舍去),
于是Q-92,-36.所以|PQ|=-2+922+(26+36)2=252.
设M-t212,t(t∈(-36,26))到直线PQ的距离为d,
则d=630×t+622-752,当t=-62时,dmax=630×752=564,
所以△MPQ面积的最大值为12×252×564=125616.
此时直线MP:y=-463x-263.
9.(2017湖南湘中名校联考)已知经过抛物线C:x2=2py焦点F的直线l:y=kx+1与抛物线C交于A,B两点,若存在一定点D(0,b),使得无论AB怎样运动,总有直线AD的斜率与BD的斜率互为相反数.
(1)求p与b的值.
(2)对于椭圆C':x25+y2=1,经过它左焦点F'的直线l'与椭圆C'交于A',B'两点,是否存在定点D',使得无论A'B'怎样运动,都有∠A'D'F'=∠B'D'F'?若存在,求出D'的坐标;若不存在,请说明理由.
【解析】(1)∵直线l:y=kx+1经过抛物线C:x2=py的焦点为F,
∴F(0,1),∴p=2.
直线y=kx+1代入x2=4y得x2-4kx-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4.
∵无论AB怎样运动,直线AD的斜率与BD的斜率互为相反数.
∴无论x1、x2怎样变化,总有x124-bx1+x224-bx2=0,即b=x1x24.
∵x1x2=-4,∴b=-1.
(2)直线l'垂直于x轴时,A'、B'两点关于x轴对称,
∵F'(-2,0),∴要使∠A'D'F'=∠B'D'F',则D'必在x轴上.设点D'(a,0),
直线l'不垂直于x轴时,设l':y=k(x+2),A(x1,y1),B(x2,y2).
将l':y=k(x+2)代入x25+y2=1,得(1+5k2)x2+20k2x+20k2-5=0.
∴x1+x2=-20k21+5k2,x1x2=20k2-51+5k2.
∵∠A'D'F'=∠B'D'F',∴直线A'D'的斜率与B'D'的斜率互为相反数.
即k(x1+2)x1-a+k(x2+2)x2-a=0,
∴a=2(x1+x2)+2x1x2x1+x2+4=2×-20k21+5k2+2×20k2-51+5k2-20k21+5k2+4
=-52.
∴存在定点D'-52,0,使得∠A'D'F'=∠B'D'F'.
10.(2017九江联考)已知抛物线y2=4x的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q,且F1P·F2Q=-5.
(1)求点T的横坐标x0;
(2)若以F1,F2为焦点的椭圆C过点1,22.
(ⅰ)求椭圆C的标准方程;
(ⅱ)过点F2作直线l与椭圆C交于A,B两点,设F2A=λF2B,若λ∈[-2,-1],求|TA+TB|的取值范围.
【解析】(1)由题意得F1(-1,0),F2(1,0),设P(x0,y0),Q(x0,-y0),
则F1P=(x0+1,y0),F2Q=(x0-1,-y0).
由F1P·F2Q=-5,得x02-1-y02=-5,即x02-y02=-4, ①
又点P(x0,y0)在抛物线上,则y02=4x0, ②
联立①②,得x0=2.
(2)(ⅰ)由已知得椭圆的半焦距c=1,设椭圆C的标准方程为x2a2+y2b2=1(a>b>0),
由椭圆过点1,22,得1a2+12b2=1.又c=1,即a2-b2=1,解得a2=2,b2=1.
故椭圆C的标准方程为x22+y2=1.
(ⅱ)容易验证直线l的斜率不为0,设直线l的方程为x=ky+1,
将直线l的方程代入x22+y2=1,得(k2+2)y2+2ky-1=0.
设A(x1,y1),B(x2,y2),y1≠0且y2≠0,则由根与系数的关系,可得y1+y2=-2kk2+2, ⑤
y1y2=-1k2+2, ⑥
因为F2A=λF2B,所以y1y2=λ,且λ<0.
由⑤⑥,得y1y2+y2y1+2=-4k2k2+2,即λ+1λ+2=-4k2k2+2.
由λ∈[-2,-1],得-12≤λ+1λ+2≤0,即-12≤-4k2k2+2≤0,
所以0≤k2≤27.
因为TA=(x1-2,y1),TB=(x2-2,y2),所以TA+TB=(x1+x2-4,y1+y2).
又因为y1+y2=-2kk2+2,所以x1+x2-4=k(y1+y2)-2=-4(k2+1)k2+2,
故|TA+TB|2=(x1+x2-4)2+(y1+y2)2
=16(k2+1)2(k2+2)2+4k2(k2+2)2
=16(k2+2)2-28(k2+2)+8(k2+2)2
=16-28k2+2+8(k2+2)2.
令t=1k2+2,因为0≤k2≤27,
所以716≤1k2+2≤12,即t∈716,12,
所以TA+TB2=f(t)=8t2-28t+16=8t-742-172∈4,16932,
所以TA+TB的取值范围为2,1328.
阶段总结六
微专题一
圆锥曲线的“焦点”访谈
椭圆(或双曲线)上任意一点与两个焦点的连线构成的三角形称为焦点三角形.常考题型是离心率、弦长、角度、面积、最值等问题.解题时一般用到定义、正弦定理或余弦定理,也涉及三个基本量间的关系,故要仔细审题,选准解题方法.
【例1】(2014年全国Ⅲ卷)已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若F1A=2F2A,则cos∠AF2F1=( ).
A.14 B.13 C.24 D.23
【分析】由定义找出a,b,c的关系,在△AF1F2中,利用余弦定理求解.
【解析】因为F1A=2F2A,设F2A=m,则F1A=2m.因为点A在双曲线C上,所以F1A-F2A=m=2a,即F2A=2a,F1A=4a.因为e=ca=2,所以c=2a,|F1F2|=2c=4a.在△AF1F2中,由余弦定理得cos∠AF2F1=|AF2|2+|F1F2|2-|AF1|22|AF2|·|F1F2|=4a2+(4a)2-(4a)22×2a×4a=14.故选A.
【答案】A
【拓展训练1】已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( ).
A.14 B.35 C.34 D.45
【解析】双曲线C:x2-y2=2的标准方程为x22-y22=1,所以a=b=2,c=2.因为|PF1|=2|PF2|,设PF2=m,则PF1=2m.因为点P在双曲线C上,所以PF1-PF2=m=2a=22,即PF2=22,PF1=42,|F1F2|=2c=4.在△PF1F2中,由余弦定理得cos∠F1PF2=|PF1|2+|PF2|2-|F1F2|22|PF1|·|PF2|=(22)2+(42)2-422×22×42=34.
【答案】C
微专题二
解析几何与向量牵手
平面向量具有代数形式和几何形式双重身份,由于向量既能体现“形”的直观位置特征,又具有“数”的良好运算性质,是数形结合与转换的桥梁和纽带.而解析几何也具有数形结合与转换的特征,所以在向量与解析几何知识的交汇处设计试题,已逐渐成为高考命题的一个新亮点.
【例2】如图,已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点为F1、F2,其上顶点为A.已知△F1AF2是边长为2的正三角形.
(1)求椭圆C的方程;
(2)过点Q(-4,0)任作一动直线l交椭圆C于M,N两点,在线段MN上取一点R,使得|MQ||QN|=|MR||RN|,试判断当直线l运动时,点R是否在某一定直线上运动?若在,请求出该定直线;若不在,请说明理由.
【分析】由已知条件得Q,M,N三点共线,R,M,N三点共线,由|MQ||QN|=|MR||RN|,故可设MQ=λQN,MR=-λRN,其中M,N是直线与椭圆的交点,所以设M(x1,y1),N(x2,y2).考虑根与系数关系,设R(x0,y0),再代入向量式,利用向量相等的充要条件,得其坐标间的关系并结合消参技巧得出x0,故点R在定直线x=x0上.
【解析】(1)△F1AF2是边长为2的正三角形,则c=1,a=2,故椭圆C的方程为x24+y23=1.
(2)直线MN的斜率必存在,设其直线方程为y=k(x+4),M(x1,y1),N(x2,y2).
联立方程x24+y23=1,y=k(x+4),消去y,得(3+4k2)x2+32k2x+64k2-12=0,则Δ=144(1-4k2)>0,x1+x2=-32k23+4k2,x1x2=64k2-123+4k2.由题意可设MR=-λRN,MQ=λQN,
由MQ=λQN,得-4-x1=λ(x2+4),故λ=-x1+4x2+4.
设点R的坐标为(x0,y0),则由MR=-λRN,得x0-x1=-λ(x2-x0),
解得x0=x1-λx21-λ=x1+x1+4x2+4·x21+x1+4x2+4=2x1x2+4(x1+x2)(x1+x2)+8.
又2x1x2+4(x1+x2)=2×64k2-123+4k2+4×-32k23+4k2=-243+4k2,
(x1+x2)+8=-32k23+4k2+8=243+4k2,从而x0=2x1x2+4(x1+x2)(x1+x2)+8=-1,
故点R在定直线x=-1上.
【拓展训练2】(2017届重庆八中月考)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为22,且以原点为圆心,椭圆的焦距为直径的圆与直线xsin θ+ycos θ-1=0相切(θ为常数).
(1)求椭圆C的标准方程;
(2)如图,若椭圆C的左、右焦点分别为F1、F2,过点F2作直线l与椭圆分别交于M、N两点,求F1M·F1N的取值范围.
【解析】(1)由题意得ca=22,1sin2θ+cos2θ=c,a2=b2+c2,解得c=1,a2=2,b2=1,
故椭圆C的标准方程为x22+y2=1.
(2)若直线l的斜率不存在,则直线l的方程为x=1,M1,22,N1,-22,
∴F1M=2,22,F1N=2,-22,故F1M·F1N=72.
若直线l的斜率存在,设直线l的方程为y=k(x-1),
由y=k(x-1),x22+y2=1,消去y,得(1+2k2)x2-4k2x+2k2-2=0.
∴x1+x2=4k21+2k2,x1x2=2k2-21+2k2.
设M(x1,y1),N(x2,y2),∴F1M=(x1+1,y1),F1N=(x2+1,y2),
则F1M·F1N=(x1+1)(x2+1)+y1y2=(x1+1)(x2+1)+k(x1-1)·k(x2-1)=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2=2(k4-1)2k2+1+4k2-4k42k2+1+1+k2=7k2-12k2+1=72-922k2+1.
由k2≥0,得F1M·F1N∈-1,72.
综上可知,F1M·F1N的取值范围为-1,72.
微专题三
浅析减少解析几何运算量的常用方法
在解决解析几何问题时,方法选择不当会导致计算量过大,若不具备较高的解析几何运算能力,也不易得到正确的运算结果.那么该如何正确地选择解题方法,从而减少解决解析几何问题的计算量呢?下面介绍两种常用的方法.
一、活用图形性质,数形结合
【例3】已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,过点F且倾斜角为60°的直线交抛物线C于A,B两点,AM⊥l,BN⊥l,M,N为垂足,点Q是MN的中点,|QF|=2,求抛物线C的方程.
【分析】因为焦点弦为AB,所以需要将条件“|QF|=2”转化为|AB|的长,再利用韦达定理和焦点弦计算公式求解.
【解析】如图,由抛物线的几何性质可得△MFN是以∠MFN为直角的直角三角形,
∴|MN|=2|QF|=4.过点B作BD⊥AM于点D,则|BD|=4,
∴|AB|=|BD|sin60°=833.
设A(x1,y1),B(x2,y2),联立y2=2px,y-0=3x-p2,
得12x2-20px+3p2=0.∴x1+x2=2012p=53p,
∴|AB|=x1+x2+p=53p+p=833,解得p=3.
故抛物线C的方程为y2=23x.
【拓展训练3】若函数f(x)=1-x2x+3-m有零点,则实数m的取值范围是( ).
A.0,22 B.0,22
C.0,24 D.0,24
【解析】令f(x)=1-x2x+3-m=0,得1-x2=m(x+3).在同一平面直角坐标系内作出y=1-x2和y=m(x+3)的图象(如图).因为函数f(x)有零点,所以直线y=m(x+3)与半圆x2+y2=1(y≥0)相交或相切,即|3m|m2+1≤1,解得0≤m≤24.
【答案】C
二、设而不求,整体运算
【例4】(2017漳州八校联考)如图,椭圆C:x2a2+y2b2=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=52|BF|.
(1)求椭圆C的离心率;
(2)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ,求椭圆C的方程.
【分析】(1)先找a,b的关系,再求关于a,c的方程,最后求出离心率;
(2)设P(x1,y1),Q(x2,y2),将直线l的方程与椭圆方程组成方程组,消去y,用b表示x,从而用b表示x1,x2,用OP⊥OQ表示x1,x2,得到关于b的方程,求出b的值.
【解析】(1)由已知|AB|=52|BF|,得a2+b2=52a,即4a2+4b2=5a2.
又∵b2=a2-c2,
∴4a2+4(a2-c2)=5a2,即3a2=4c2,
∴e=ca=32.
(2)由(1)知a2=4b2,∴椭圆C的标准方程为x24b2+y2b2=1.
设P(x1,y1),Q(x2,y2),直线l的方程为y-2=2(x-0),即2x-y+2=0.
由2x-y+2=0,x24b2+y2b2=1,得x2+4(2x+2)2-4b2=0,
即17x2+32x+16-4b2=0.
由Δ=322+16×17(b2-4)>0,得b>21717.
∴x1+x2=-3217,x1x2=16-4b217.
∵OP⊥OQ,∴OP·OQ=0,
即x1x2+y1y2=x1x2+(2x1+2)(2x2+2)=5x1x2+4(x1+x2)+4=0.
∴5(16-4b2)17-12817+4=0,解得b=1,
∴椭圆C的方程为x24+y2=1.
【拓展训练4】(2017年天津卷)设椭圆x2a2+y2b2=1(a>b>0)的左焦点为F,右顶点为A,离心率为12.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为12.
(1)求椭圆的方程和抛物线的方程;
(2)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(点B异于点A),直线BQ与x轴相交于点D.若△APD的面积为62,求直线AP的方程.
【解析】(1)依题意设点F(-c,0),
则e=ca=12,且p2=a.
由对称性知抛物线的准线l的方程为x=-a,
所以a-c=12,解得a=1,c=12,p=2,
所以b2=a2-c2=34.
故椭圆的方程为x2+4y23=1,抛物线的方程为y2=4x.
(2)由于准线l的方程为x=-1,依题意设P(-1,t)(t≠0),则Q(-1,-t).因为A(1,0),
所以kAP=12,得直线AP的方程为y=-t2(x-1). ①
将①式代入方程3x2+4y2=3中,化简得(t2+3)x2-2t2x+t2-3=0.设点B(x0,y0),由韦达定理得x0=x0xA=t2-3t2+3,则y0=-t2(x0-1)=3tt2+3,即Bt2-3t2+3,3tt2+3,则kBQ=t2+62t,于是直线BQ的方程为y+t=t2+62t(x+1).
令y=0,得x=t2-6t2+6,即Dt2-6t2+6,0,则|AD|=1-t2-6t2+6=12t2+6,
于是S△APD=12·12t2+6·|t|=62,化简得(|t|-6)2=0,解得t=±6.代入①式,化简得直线AP的方程为3x+6y-3=0或3x-6y-3=0.
微专题四
自主招生真题赏析
本专题供参加自主招生考试的学生使用
1.已知点A(-2,0),B(0,2),若点C是圆x2-2x+y2=0上的一个动点,求△ABC面积的最小值.
【解析】由题意知圆的方程可化为(x-1)2+y2=1.
设点C(1+cos θ,sin θ)到直线AB:x-y+2=0的距离为d,则d=|1+cosθ-sinθ+2|2=|cosθ-sinθ+3|2.
又cos θ-sin θ=2cosθ+π4∈[-2,2],所以dmin=3-22.
因此,(S△ABC)min=12×22×3-22=3-2.
当C点的坐标取1-22,22时,△ABC的面积最小,面积的最小值为3-2.
2.已知抛物线的顶点在原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点.若BC边所在直线的方程为4x+y-20=0,则抛物线的方程为( ).
A.y2=16x B.y2=8x
C.y2=-16x D.y2=-8x
【解析】如图,令方程为y2=2px(p>0).
设Ay122p,y1,By222p,y2,Cy322p,y3.
由y2=2px,4x+y-20=0得y2=2p·20-y4.
所以4y2=40p-2py,2y2+py-20p=0.
又y2+y3=-p2,y2y3=-10p,
依题意, y122p+y222p+y322p=32p,y1+y2+y3=0,
所以 y2+y3=-p2, ①y2y3=-10p,②y1+y2+y3=0,③y12+y22+y32=3p2.④
由①③得y1=p2,代入④中,y22+y32=114p2.
另一方面,由①②得y22+y32=p24+20p.
所以114p2=14p2+20p,解得p=8(p=0舍去).
所以抛物线方程为y2=16x.
【答案】A
3.如图,已知椭圆C:x2a2+y2b2=1(a>b>0)的一个焦点到长轴的两个端点的距离分别为2+3和2-3,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(1)求此椭圆的方程;
(2)若ED=6DF,求k的值;
(3)求四边形AEBF面积的最大值.
【解析】(1)由题意得a+c=2+3,a-c=2-3,解得a=2,c=3,b=1,所以所求的椭圆方程是x24+y2=1.
(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1
由D在AB上知x0+2kx0=2,得x0=21+2k.
所以21+2k=1071+4k2,化简得24k2-25k+6=0,解得k=23或k=38.
(3)根据点到直线的距离公式和①式,可知点E、F到直线AB的距离分别是
h1=|x1+2kx1-2|5=2(1+2k+1+4k2)5(1+4k2),
h2=|x2+2kx2-2|5=2(1+2k-1+4k2)5(1+4k2).
又|AB|=22+1=5,所以四边形AEBF的面积为S=12|AB|(h1+h2)=12·5·4(1+2k)5(1+4k2)=2(1+2k)1+4k2=21+4k2+4k1+4k2≤22.
故当k=12时,四边形AEBF的面积最大,面积的最大值为22.
4.如图,已知动直线l经过点P(4,0),且交抛物线y2=2ax(a>0)于A、B两点,坐标原点O是PQ的中点,设直线AQ,BQ的斜率分别为kAQ,kBQ.
(1)证明:kAQ+kBQ=0.
(2)当a=2时,是否存在垂直于x轴的直线l',被以AP为直径的圆截得的弦长为定值?若存在,请求出直线l'的方程;若不存在,请说明理由.
【解析】设A(x1,y1),B(x2,y2).
(1)(法一)直线AQ交抛物线于点C(x3,y3),
设直线AQ:x=k1y-4,直线AB:x=k2y+4.
先将x=k2y+4代入y2=2ax中,整理得y2-2ak2y-8a=0,
所以y1y2=-8a.
同理可得y1y3=8a.所以y2=-y3.
因此点B与点C关于x轴对称,即lAQ与lBQ关于x轴对称.
所以kAQ+kBQ=0.
(法二)设直线AB:x=ky+4.将x=ky+4代入y2=2ax中,得y2-2aky-8a=0,
又y1+y2=2ak,y1y2=-8a,所以QA=(ky1+8,y1),QB=(ky2+8,y2),
kQA+kQB=y1ky1+8+y2ky2+8=2ky1y2+8(y1+y2)(ky1+8)(ky2+8)=-16ak+16ak(ky1+8)(ky2+8)=0.
(
2)由a=2知抛物线方程为y2=4x,那么可设Ay24,y.又P点坐标为(4,0),所以线段AP的中点O'的坐标可表示为
O'y2+168,y2(如图).设圆的半径为r,则r=|O'P|=y2+168-42+y24.
再设直线l'存在,方程为x=t.
设O'到l'的距离为d,那么要使被以AP为直径的圆截得的弦长为定值C,
则r2-d2=C22
⇒y2+168-42+y24-t-y2+1682=C22
⇒-t2+y2+164t-34y2=C22
⇒t4-34y2-t2+4t=C22
⇒t4=34即t=3.
所以直线l'存在,方程为x=3.
阶段检测六
一、选择题
1.(2017河北质检)“0≤k<3”是“方程x2k+1+y2k-5=1表示双曲线”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】∵0≤k<3,∴k+1>0,k-5<0,∴方程x2k+1+y2k-5=1表示双曲线,
反之,∵方程x2k+1+y2k-5=1表示双曲线,∴(k+1)(k-5)<0,解得-1
【答案】A
2.(2017武汉3月模拟)已知焦点为F的抛物线C:y2=2px过圆Ω:x2+y2-4x+2y=0的圆心,若点M(x0,4)在抛物线C上,则MF=( ).
A.2578 B.1294 C.5 D.10
【解析】依题意,圆Ω:x2+y2-4x+2y=0的圆心为(2,-1),代入抛物线C:y2=2px中,得2p=12,故y2=12x.将点M(x0,4)代入可得x0=32,由抛物线定义可知MF=32+18=2578.
【答案】A
3.(2017巢湖联考)已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( ).
A.相切 B.相交 C.相离 D.不确定
【解析】∵点M(a,b)在圆x2+y2=1外,∴a2+b2>1,∴点O(0,0)到直线ax+by=1的距离d=1a2+b2<1=r,则直线与圆的位置关系是相交.故选B.
【答案】B
4.(2017西安质检)已知双曲线x2a2-y2b2=1的一个焦点与抛物线y2=410x的焦点重合,且双曲线的离心率等于103,则双曲线的方程为( ).
A.x2-y29=1 B.x2-y2=1
C.x29-y29=1 D.x29-y2=1
【解析】由题意可得双曲线的一个焦点为(10,0),所以c=10.由ca=103,得a=3,所以b2=c2-a2=1,故双曲线的方程为x29-y2=1,故选D.
【答案】D
5.(2017盘锦期中)已知椭圆的两个焦点为F1(-5,0),F2(5,0),P是此椭圆上的一点,且PF1⊥PF2,|PF1|·|PF2|=2,则该椭圆的方程是( ).
A.x26+y2=1 B.x24+y2=1
C.x2+y26=1 D.x2+y24=1
【解析】如图,由已知条件知,|PF1|2+|PF2|2=20,
∵|PF1||PF2|=2,
∴|PF1|2+2|PF1||PF2|+|PF2|2=(|PF1|+|PF2|)2=4a2=24.
∴a2=6,b2=6-5=1,∴椭圆的标准方程为x26+y2=1.故选A.
【答案】A
6.(2017上海质检)在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是( ).
A.0,43 B.0,43
C.0,43 D.0,43
【解析】设直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆为圆M,
又圆C的标准方程为(x-4)2+y2=1,则圆心C的坐标为(4,0),半径R=1,如图.若圆M与圆C有公共点,则圆M与圆C的临界点为圆M与圆C的外切点,即等价为圆心C到直线y=kx-2的距离d≤R+1=2,即d=|4k-2|1+k2≤2,
即|2k-1|≤1+k2,解得0≤k≤43,故选A.
【答案】A
7.(2017珠海模拟)如图,“嫦娥三号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1-c1=a2-c2;
③c1a2>a1c2;④c1a1
A.①③ B.②③ C.①④ D.②④
【解析】由题意知a1>a2,在椭圆轨道Ⅰ中,PF=a1-c1,在椭圆轨道Ⅱ中,PF=a2-c2,则有a1-c1=a2-c2,故②正确.由a1>a2,得1a1<1a2,则a1-c1a1
【答案】B
8.(2017惠安模拟)已知抛物线y=18x2与双曲线y2a2-x2=1(a>0)有共同的焦点F,O为坐标原点,点P在x轴上方且在双曲线上,则OP·FP的最小值为( ).
A.3-23 B.23-3 C.-74 D.34
【解析】抛物线的标准方程为x2=8y,焦点F为(0,2),则双曲线y2a2-x2=1(a>0)的半焦距c=2,
则a2=3,即双曲线的方程为y23-x2=1.
设P(m,n)(n≥3),则m2=13n2-1,
则OP·FP=(m,n)(m,n-2)=m2+n2-2n=13n2-1+n2-2n=43n-342-74.
因为n≥3,故当n=3时取得最小值,最小值为3-23,故选A.
【答案】A
9.(2016河南焦作一模)已知椭圆x2a2+y2b2=1(a>b>0),P为椭圆上与长轴端点不重合的一点,F1、F2分别为椭圆的左、右焦点,过点F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则a2+e22b的最小值为( ).
A.32 B.62 C.3 D.1
【解析】如图,设∠F1PF2的外角平分线为PT,则F2Q⊥PT,延长F2Q交F1P的延长线于点M.∵PT为∠F2PM的平分线,且PQ⊥F2M,∴△F2PM为等腰三角形,且|PM|=|PF2|,
由椭圆定义知|PF1|+|PF2|=2a,∴|PM|+|PF1|=|F1M|=2a.
∵O为F1F2的中点,Q为F2M的中点,
∴|OQ|=12|F1M|,∴|OQ|=a.又∵|OQ|=2b,
∴a=2b,∴e=1-b2a2=32.
∴a2+e22b=4b2+342b=2b+38b≥22b·38b=3,
当且仅当2b=38b,即b=34时取等号,故选C.
【答案】C
二、填空题
10.(2017河南联考)已知焦点为F的抛物线y2=4x的弦AB的中点的横坐标为2,则|AB|的最大值为 .
【解析】设A(x1,y1),B(x2,y2),则x1+x2=4,|AF|+|BF|=x1+x2+2.
又|AF|+|BF|≥|AB|⇒|AB|≤6,故当AB过焦点F时取得最大值6.
【答案】6
11.(2017宜昌调研)过椭圆x25+y24=1的右焦点作一条斜率为2的直线与椭圆交于A,B两点,O为坐标原点,则△OAB的面积为 .
【解析】由题意知椭圆的右焦点F的坐标为(1,0),则直线AB的方程为y=2x-2.联立x25+y24=1,y=2x-2,解得交点A(0,-2),B53,43,所以S△OAB=12|OF||yA-yB|=12×1×-2-43=53.
【答案】53
12.(2017石室中学高考模拟二)设F1、F2是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,P是双曲线右支上一点,满足(OP+OF2)·PF2=0(O为坐标原点),且3|PF1|=4|PF2|,则双曲线的离心率为 .
【解析】因为点P在双曲线的右支上,则由双曲线的定义可得|PF1|-|PF2|=2a.
又|PF1|=43|PF2|,解得|PF1|=8a,|PF2|=6a.
由(OP+OF2)·PF2=0,即(OP+OF2)·(OF2-OP)=0,得OP2=OF2.
则在△PF1F2中,|OP|=|OF2|=|OF1|,则∠F1PF2=90°.
由勾股定理得|PF1|2+|PF2|2=|F1F2|2,即64a2+36a2=4c2,则c=5a,所以e=ca=5.
【答案】5
13.(2017湖北省六校联考)从椭圆y2a2+x2b2=1(2b≥a>b>0)上的动点M作圆x2+y2=b22的两条切线,切点为P和Q,直线PQ与x轴和y轴的交点分别为E和F,则△EOF面积的最小值是 .(用字母a,b表示)
【解析】设M(x0,y0),P(x1,y1),Q(x2,y2),直线MP和MQ的方程分别为x1x+y1y=b22,x2x+y2y=b22.
因为点M在直线MP和直线MQ上,所以x1x0+y1y0=b22,x2x0+y2y0=b22.可知P,Q两点坐标满足方程x0x+y0y=b22,所以直线PQ的方程为x0x+y0y=b22,可得直线PQ与x轴和y轴的交点分别为Eb22x0,0和F0,b22y0,所以△EOF的面积是S△EOF=12|OE||OF|=b48|x0y0|.
因为b2y02+a2x02=a2b2,又b2y02+a2x02≥2ab|x0y0|,所以|x0y0|≤ab2.
所以S△EOF=b48|x0y0|≥b34a,当且仅当b2y02=a2x02=a2b22时,△EOF面积取得最小值b34a.
【答案】b34a
三、解答题
14.(2018届郑州一中第二次月考)已知椭圆C:x2a2+y2b2=1(a>b>0)的左焦点F和上顶点B在直线3x-3y+3=0上,A为椭圆上位于x轴上方的一点且AF⊥x轴,M,N为椭圆C上不同于A的两点,且∠MAF=∠NAF.
(1)求椭圆C的标准方程;
(2)设直线MN与y轴交于点D(0,d),求实数d的取值范围.
【解析】(1)依题意得椭圆C的左焦点为F(-1,0),上顶点为B(0,3),
故c=1,b=3,所以a=b2+c2=2,
所以椭圆C的标准方程为x24+y23=1.
(2)设直线AM的斜率为k,因为∠MAF=∠NAF,所以AM,AN关于直线AF对称,所以直线AN的斜率为-k.
易知A-1,32,所以直线AM的方程是y-32=k(x+1),
联立y-32=k(x+1),x24+y23=1,消去y,得(3+4k2)x2+(12+8k)kx+(4k2+12k-3)=0,
设M(x1,y1),N(x2,y2),
所以x1=-4k2-12k+33+4k2.
将上式中的k换成-k,得x2=-4k2+12k+33+4k2,
所以kMN=y1-y2x1-x2=k[(x1+x2)+2]x1-x2=k-8k2+63+4k2+2-24k3+4k2=-12,
所以直线MN的方程是y=-12x+d.
代入椭圆方程x24+y23=1,得x2-dx+d2-3=0,
所以Δ=(-d)2-4(d2-3)>0,解得-2
解得d<1.
综上可知,实数d的取值范围是-2
一、选择题
1.(2017广东汕头市期末)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( ).
A.-43 B.-34 C.3 D.2
【解析】由题意知,圆心为(1,4),则有|a+4-1|a2+1=1,解得a=-43,故选A.
【答案】A
2.(2017广西南宁、柳州、玉林联考)已知a=1,b=2,a·(b-a)=0,则向量a与b的夹角为( ).
A.5π6 B.2π3 C.π3 D.π6
【解析】由a·(b-a)=a·b-a2=a·b-1=0,得a·b=1.
【答案】C
3.已知双曲线C:x2m-y2n=1,曲线f(x)=ex在点(0,1)处的切线方程为2mx-ny+1=0,则该双曲线的渐近线方程为( ).
A.y=±2x B.y=±2x
C.y=±22x D.y=±12x
【解析】由题得,切线方程为x-y+1=0,∴2m=1,-n=-1,∴m=12,n=1.∴双曲线的方程为x212-y2=1.∴渐近线方程为y=±2x.
【答案】A
4.(2017山西临汾一中等五校联考)实数x,y满足x-y+1≥0,x+y-3≥0,2x+y-7≤0,若x-2y≥m恒成立,则实数m的取值范围是( ).
A.(-∞,-3] B.(-∞,-4]
C.(-∞,6] D.[0,6]
【解析】x,y满足的区域如图所示.设z=x-2y,则当经过图中的A时最小,由x-y+1=0,2x+y-7=0,得A(2,3),所以z的最小值为z=2-2×3=-4,所以实数m的取值范围是(-∞,-4],故选B.
【答案】B
5.(2017湖北省部分重点中学联考)已知ω>0,函数f(x)=sinωx+π4在π2,π上单调递减,则ω的取值范围是( ).
A.12,54 B.12,34
C.0,12 D.(0,2]
【解析】∵x∈π2,π,ω>0,∴ωx+π4∈12ωπ+π4,ωπ+π4.∵函数f(x)=sinωx+π4在π2,π上单调递减,∴周期T=2πω≥π,解得ω≤2.∵f(x)=sinωx+π4的减区间满足π2+2kπ<ωx+π4<3π2+2kπ,k∈Z,∴取k=0,得12ωπ+π4≥π2,ωπ+π4≤3π2,解得12≤ω≤54,故选A.
【答案】A
6.(2017泉州适应性考试)如图,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B,P是“六芒星”(如图)的三个顶点,若OP=xOA+yOB,则x+y的值是( ).
A.3 B.4 C.5 D.6
【解析】建立如图所示的平面直角坐标系,令正三角形边长为3,
则OB=i,OA=-32i+32j,可得i=OB,j=233OA+3 OB.
由图知当点P在点C时,有OP=3j=2OA+3OB,所以x+y=5.
故选C.
【答案】C
7.(2017哈尔滨六中一模)已知矩形ABCD中,AB=6,BC=4,E,F分别是AB,CD上的动点,且AE=DF,把四边形BCFE沿EF折起,使平面BCFE⊥平面ABCD,若折得的几何体的体积最大,则该几何体外接球的体积为( ).
A.28π B.287π3 C.32π D.642π3
【解析】画出折得的几何体(直三棱柱)如图,设DF=x,FC=6-x,则DC=x2-(6-x)2=12x-36,则底面面积S△DFC=1212x-36(6-x)=3x-3(6-x).因为高为4(定值),所以只要求出g(x)=x-3(6-x)的最大值时,折得的几何体的体积最大.令x-3=t,得x=t2+3,6-x=3-t2,则g(x)=f(t)=t(3-t2)=-t3+3t,求导可得f'(t)=-3(t2-1)=-3(t+1)(t-1),故当t=1⇒x=4,即DC=23时,几何体的体积最大,此时底面外接圆的半径r=2.设外接球的球心为O,则点O到底面的距离d=2,所以球的半径R=d2+r2=4+4=22,则外接球的体积V=43π(22)3=64π23,故选D.
【答案】D
8.(2017吉安模拟)已知椭圆x2a2+y2b2=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈π6,π4,则该椭圆离心率e的取值范围为( ).
A.22,3-1 B.22,1
C.22,32 D.33,63
【解析】∵点B和A关于原点对称,∴点B也在椭圆上.设左焦点为F',
根据椭圆定义|AF|+|AF'|=2a,又∵|AF'|=|BF|,
∴|AF|+|BF|=2a. ①
∵O是Rt△ABF斜边的中点,∴|AB|=2c.
又∵|AF|=2csin α, ②
|BF|=2ccos α, ③
将②③代入①,得2csin α+2ccos α=2a,
∴ca=1sinα+cosα=12sinα+π4,
即e=12sinα+π4,α∈π6,π4.
∴5π12≤α+π4≤π2,6+24≤sinα+π4≤1,
∴22≤e≤3-1.故选A.
【答案】A
二、填空题
9.(2017贵州模拟)已知向量a=(-1,2),b=(2,y),且a∥b,则3a+2b等于 .
【解析】因为a=(-1,2),b=(2,y),且a∥b,所以(-1)×y-2×2=0,则y=-4,故3a+2b=3(-1,2)+2(2,-4)=(1,-2).
【答案】(1,-2)
10.(2017安徽省江南十校联考)中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.如图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正(主)视图和侧(左)视图为等腰梯形),则此“斗”的体积(单位:立方厘米)等于 .
【解析】由三视图可知该几何体是一个上下底面都为正方形的四棱台,其体积V=13×(400+100+200)×12=2800.
【答案】2800
11.(2017西安联考)已知数列an满足a1=0,数列bn为等差数列,且an+1=an+bn,b15+b16=15,则a31= .
【解析】由题设可得bn=an+1-an,则a2-a1=b1,a3-a2=b2,a4-a3=b3,…,a31-a30=b30,将以上30个等式两边相加,可得a31-a1=b1+b2+…+b30=15(b15+b16)=225.因为a1=0,所以a31=225.
【答案】225
12.(2017南京联考)已知抛物线C:y2=8x,点P(0,4),点A在抛物线上,当点A到抛物线准线l的距离与点A到点P的距离之和最小时,延长AF交抛物线于点B,则△AOB的面积为 .
【解析】由题可知,当点A到抛物线准线l的距离与点A到点P的距离之和最小时,由抛物线性质得抛物线上一点到准线的距离等于到焦点的距离,所以当P、A、F三点共线时达到最小值.由P(0,4)、F(2,0),可得lAB:2x+y-4=0,联立抛物线方程,可得x2-6x+4=0.设点A(x1,y1),B(x2,y2),故|AB|=x1+x2+p=6+4=10,原点到直线lAB:2x+y-4=0的距离为d=44+1=455,所以△AOB的面积为455×10×12=45.
【答案】45
三、解答题
13.(2018齐鲁名校教科研协作体联考)在△ABC中,a,b,c分别是内角A,B,C的对边,且满足(2c-a)cos B-bcos A=0.
(1)求角B的大小;
(2)若b=2,且sin B+sin(C-A)=2sin 2A,求△ABC的面积.
【解析】(1)在△ABC中,∵(2c-a)cos B-bcos A=0,
∴2sin Ccos B-sin Acos B-sin Bcos A=0,
即2sin Ccos B-sin(A+B)=0,即sin C(2cos B-1)=0.
∵sin C≠0,∴cos B=12.
∵B∈(0,π),∴B=π3.
(2)在△ABC中,A+B+C=π,即B=π-(A+C),故sin B=sin(A+C),
由sin B+sin(C-A)=2sin 2A,可得sin(A+C)+sin(C-A)=2sin 2A,
∴sin Acos C+cos Asin C+sin Ccos A-cos Csin A=4sin Acos A,
整理得cos Asin C=2sin Acos A.
若cos A=0,则A=π2.
由b=2,得c=2tanB=233,
此时△ABC的面积为S=12bc=233.
若cos A≠0,则sin C=2sin A,
由正弦定理可知,c=2a,
代入a2+c2-b2=ac,整理可得3a2=4,解得a=233,∴c=433,
此时△ABC的面积为S=12acsin B=233.
综上所述,△ABC的面积为233.
14.(2017沈阳质检)已知平面内一动点M与两定点B1(0,-1)和B2(0,1)连线的斜率之积等于-12.
(1)求动点M的轨迹E的方程;
(2)设直线l:y=x+m(m≠0)与轨迹E交于A、B两点,线段AB的垂直平分线交x轴于点P,当m变化时,求△PAB面积的最大值.
【解析】(1)设点M的坐标为(x,y),依题意得y+1x·y-1x=-12,
化简得动点M的轨迹E的方程为x22+y2=1(x≠0).
(2)设A(x1,y1),B(x2,y2),
联立方程组x22+y2=1(x≠0),y=x+m,
化简得3x2+4mx+2m2-2=0.
∵有两个不同的交点,
∴Δ=(4m)2-12(2m2-2)>0,即-3
设线段AB的中点为C,∴xC=x1+x22=-2m3,yC=xC+m=m3,即点C的坐标为-2m3,m3,
∴线段AB的垂直平分线方程为y-m3=-x+2m3.
∴点P的坐标为-m3,0.
又点P到AB的距离d=23m2,
AB=2·(x1+x2)2-4x1x2=2324-8m2,
∴S△PAB=12×23m2×23·24-8m2
=229m2(3-m2)≤229·m2+3-m22=23,
当且仅当m2=32,即m=±62∈(-3,3)时等号成立,
∴(S△PAB)max=23.
全国版高考数学必刷题:第十五单元 直线和圆的方程: 这是一份全国版高考数学必刷题:第十五单元 直线和圆的方程,共41页。试卷主要包含了已知平行直线l1,已知圆M,若圆C1等内容,欢迎下载使用。
全国版高考数学必刷题:第九单元 平面向量: 这是一份全国版高考数学必刷题:第九单元 平面向量,共57页。
全国版高考数学必刷题:第十八单元 统计初步: 这是一份全国版高考数学必刷题:第十八单元 统计初步,共42页。试卷主要包含了32,∑i=17tiyi=40,1 随机抽样与样本分布等内容,欢迎下载使用。












