2018年中考数学（全国）总复习精英课件： 第二轮专题总复习 专题一 第4节　动点或最值问题 (共25张PPT)

这是一份2018年中考数学（全国）总复习精英课件： 第二轮专题总复习 专题一 第4节　动点或最值问题 (共25张PPT)，共25页。PPT课件主要包含了≤CD≤5等内容，欢迎下载使用。

动点或最值问题在中考中涉及不多，但此类问题综合性较强，题目难度较大，常以选择题或填空题中压轴题的形式出现，有时也和解答题中的压轴题结合在一起，常和二次函数、几何图形等知识结合起来考查．在最近几年的中考中，此类题型频率逐渐增大，预计2018年中考继续考查的可能性非常大．
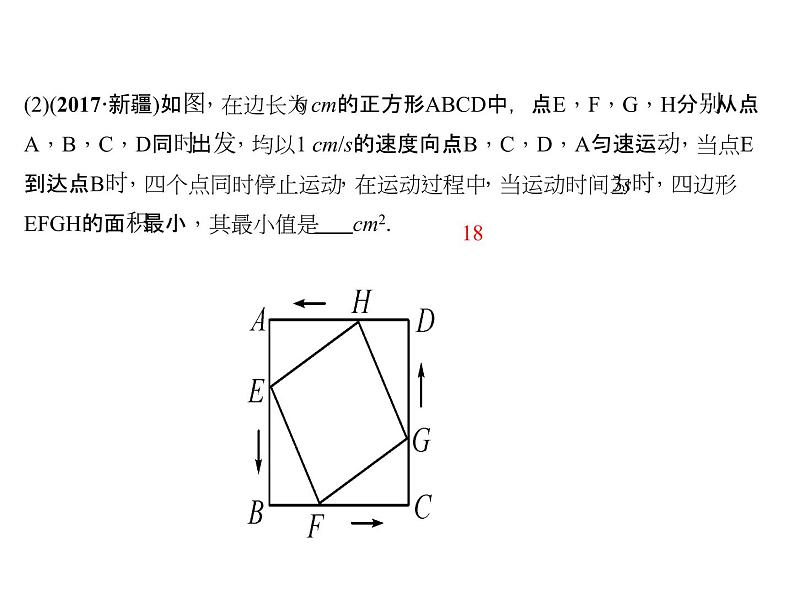
(2)(2017·新疆)如图，在边长为6 cm的正方形ABCD中，点E，F，G，H分别从点A，B，C，D同时出发，均以1 cm/s的速度向点B，C，D，A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为3s时，四边形EFGH的面积最小，其最小值是 cm2.
【思路引导】(1)作CE′⊥AB于点E′，交BD于点P′，连接AC，AP′.首先证明E′与E重合，因为点A，C关于BD对称，所以当P与P′重合时，PA′＋P′E的值最小，由此求出CE.(2)设运动时间为t(0≤t≤6)，则AE＝t，AH＝6－t，由四边形EFGH的面积＝正方形ABCD的面积－4个△AEH的面积，即可得出S四边形EFGH关于t的函数关系式，配方后即可得出结论．
求线段和最短，若已知两点在动点所在直线的同侧，将动点所在直线作为对称轴，作出其中一点的对称点，再将另一点与所作的对称点连接，则其与直线的交点即为所求动点所在位置，则所连接的线段长即为所求的最短线段和．
3．(导学号65244218)(2016·娄底)如图，在Rt△ABC中，∠ABC＝90°，点D沿BC自B向C运动(点D与点B，C不重合)，作BE⊥AD于点E，CF⊥AD于点F，则BE＋CF的值（ ）A．不变 B．增大C．减小 D．先变大再变小
7．(导学号65244222)(2017·贵港)如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM.若BC＝2，∠BAC＝30°，则线段PM的最大值是（ ）A．4 B．3 C. 2 D．1
9．(导学号65244224)(2017·眉山)△ABC是等边三角形，点O是三条高的交点．若△ABC以点O为旋转中心旋转后能与原来的图形重合，则△ABC旋转的最小角度是 ．
10．(导学号65244225)(2017·常德)如图，在Rt△ABE中，∠A＝90°，∠B＝60°，BE＝10，D是线段AE上的一动点，过点D作CD交BE于点C，并使得∠CDE＝30°，则CD长度的取值范围是 .
11．(导学号65244226)(2016·泸州)如图，在平面直角坐标系中，已知点A(1，0)，B(1－a，0)，C(1＋a，0)(a＞0)，点P在以点D(4，4)为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则a的最大值是 ．