初中数学鲁教版 (五四制)九年级下册3 垂径定理精品课后练习题

鲁教版九年级下册5.3垂径定理同步课时训练

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．如图，在⊙O中，弦AB的长是半径OA的倍，C为中点，AB、OC交于点P，则四边形OACB是（   ）

A．平行四边形 B．矩形 C．菱形 D．正方形

2．如图，是的弦（非直径），点是弦上的动点（不与点，重合），过点作垂直于的弦．若设的半径为，弦的长为，，则弦的长（  ）

A．与，，的值均有关 B．只与，的值有关

C．只与，的值有关 D．只与，的值有关

3．如图，的半径为5，弦，P是弦AB上的一个动点（不与A，B重合），下列符合条件的OP的值是（     ） 

A．6.5 B．5.5 C．3. D．2.5

4．如图，，边上有一点D，，以点D为圆心，以长为半径作弧交于点E，则（    ）

A． B．4 C． D．8

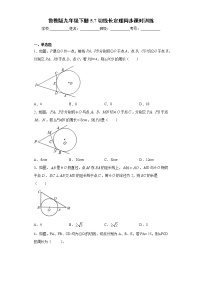
5．如图，中，，以点为圆心，为半径作圆，交的延长线于点，则长为（    ）

A．10 B．9 C． D．8

6．一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（   ）

A．1 B．2 C．3 D．4

7．“圆材埋壁”是我国古代数学名著《章算术》中的一个问题：“今有圆材埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺问：径几何？”转化为数学语言：如图，为的直径，弦，垂足为，寸，寸，直径的长是（   ）

A．寸 B．寸 C．寸 D．寸

8．往直径为的圆柱形容器内装入一些水以后，截面如图所示，若水的最大深度为，则水面的宽度为（    ）

A． B． C． D．

9．如图，EM经过圆心O，EM⊥CD于M，若CD=4，EM=6，则弧CED所在圆的半径为（　　）

A．3 B．4 C． D．

10．往直径为26cm的圆柱形容器内装入一些水以后，截面如图所示．若水面宽，则水的最大深度为（ ）

A．4cm B．5cm C．8cm D．10cm

二、填空题

11．如图，点为的半径的中点，弦过点且垂直于，若，则弦的长为______．

12．如图，AB，CD是半径为15的⊙O的两条弦，AB＝24，CD＝18，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上任意一点，则PA＋PC的最小值为_____．

13．如图平面直角坐标系中，⊙O的半径5，弦AB的长为4，过点O做OC⊥AB于点C，⊙O内一点D的坐标为（﹣4，3），当弦AB绕点O顺时针旋转时，点D到AB的距离的最小值是_____．

14．已知是的弦，，于点C，，则的半径是______．

15．如图，与抛物线交于两点，且，则的半径等于___________．

16．如图，半径为的中有弦，以为折痕对折，劣弧恰好经过圆心，则弦的长度为__________．

三、解答题

17．如图，已知AB是⊙O的直径，C是半圆上一点(不与点A，B重合)

（1）用尺规过点C作AB的垂线交⊙O于点D(保留作图痕迹，不写作法)；

（2）若AC=4，BC=2，求（1）中所作的弦CD的长．

18．如图，在中，．点在边上，，以为圆心，为半径的弧经过点．是弧上的一个动点．

（1）求线段的长；

（2）若是弧的中点，连接，求的正切值；

（3）若平分，延长交的延长线于点，求线段的长．

19．（1）解方程：；

（2）已知：如图，的直径与弦（不是直径）交于点F，若FB=2，CF=FD=4，设的半径为r，求的长．

20．如图，点C、D分别在扇形AOB的半径OA、OB的延长线上，且OA=5，AC=3，CD平行于AB，与弧AB相交于点M、N．

（1）求线段OD的长；

（2）若tan∠C=，求弦MN的长．

参考答案

1．C

2．D

3．C

4．A

5．B

6．A

7．B

8．D

9．D

10．C

11．

12．

13．6

14．5

15．

16．

17．（1）作图见解析；（2）

【详解】

解：（1）如图，CD为所作，且CD与AB交于E；

（2）由勾股定理可得：

，

∴由三角形面积求法可得：

，
 

∴CD=2CE= ．

18．（1）；（2）；（3）

【详解】

解：（1）

如图1，过点作于点，

则，

∵，，

∴△BHO∽△BCA，

∴，

∴，

∴，

在中，，

∴；

（2）

如图2，连接交于点，过点作于点，

∵是弧的中点，

∴，

在中，，

在与中，，

∴△POE≌△BOH（AAS），

∴，

∴，

∴的正切值为．

（3）

如图3，过点作于点，

∵平分，，

∴，

∵，

∴，

∴．

设，

∴，

∴，

在与中，

∴，

∴，

∵，

∴，

解得（舍去）或，

∴．

过点作交于点，

则，

∴，

∴，

∴，

∴，

∴．

19．（1）；（2）．

【详解】

（1）解：，

∴，

∴，

解得：；

（2）解：连接，如图：

∵是直径，，

∴，

∴，

即，

∴，

∴由勾股定理得

．

20．（1）OD=8；（2）

【详解】

解：（1）∵CD∥AB，
∴∠OAB=∠OCD，∠OBA=∠ODC，
∴△OAB∽△OCD，
∴，
即，
又OA=5，AC=3，
∴OB=3，
∴，

；

（2）如图，过O作OE⊥CD，连接OM，则ME=MN，

∵tan∠C= ，即 ，
∴设 ，则 ，
在Rt△OEC中，，即，解得，

，
在Rt△OME中， ，即，解得．
∴ ．