2020--2021年中考数学一轮突破 基础过关 第16讲二次函数

这是一份2020--2021年中考数学一轮突破 基础过关 第16讲二次函数，共46页。试卷主要包含了二次函数的概念，二次函数的基本形式，二次函数图象及图象的变换等内容，欢迎下载使用。

第16讲　二次函数

课标要求
(1)通过对实际问题的分析，体会二次函数的意义．
(2)会用描点法画出二次函数的图像，通过图像了解二次函数的性质．
(3)会用配方法将数字系数的二次函数的表达式化为y＝a(x－h)2＋k的形式，并能由此得到二次函数图像的顶点坐标，说出图像的开口方向，画出图像的对称轴，并能解决简单实际问题．
(4)会利用二次函数的图像求一元二次方程的近似解．
(5)*知道给定不共线三点的坐标可以确定一个二次函数.
考情分析
　　该内容主要是以填空、选择、二次函数综合题的形式来考查，特别是二次函数综合题居多，分值为3～15分．主要考点为二次函数的图象及性质、确定二次函数的表达式、二次函数与一元二次方程及不等式的关系、二次函数与图形的综合等．预测2021年中考以上考点依然会出现，建议加强理解图象与性质，熟练题型与方法，并加以练习巩固.
第1课时


一、二次函数的概念
一般地，形如______________(a，b，c是常数，且a________)的函数，叫做二次函数．
二、二次函数的基本形式
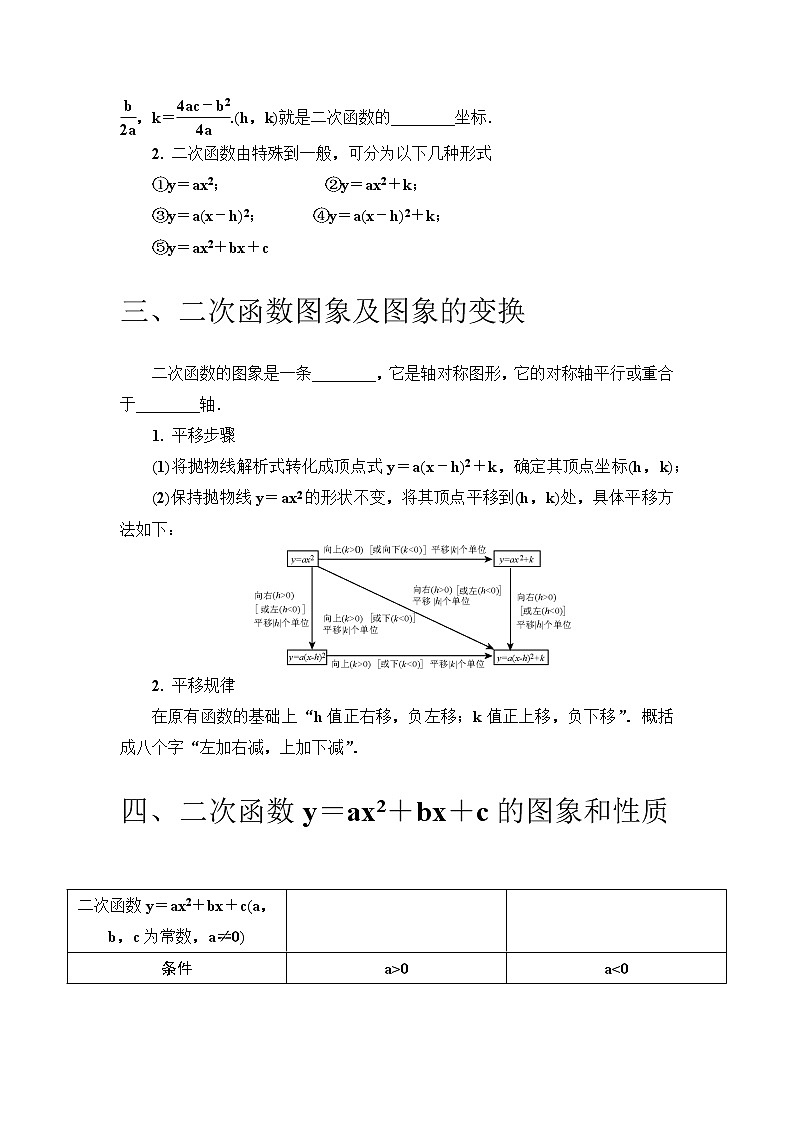
1. 二次函数y＝ax2＋bx＋c用配方法可化成y＝a(x－h)2＋k的形式，其中h＝－，k＝.(h，k)就是二次函数的________坐标．
2. 二次函数由特殊到一般，可分为以下几种形式
①y＝ax2；　　　　　　②y＝ax2＋k；
③y＝a(x－h)2；　　　④y＝a(x－h)2＋k；
⑤y＝ax2＋bx＋c
三、二次函数图象及图象的变换
二次函数的图象是一条________，它是轴对称图形，它的对称轴平行或重合于________轴．
1. 平移步骤
(1)将抛物线解析式转化成顶点式y＝a(x－h)2＋k，确定其顶点坐标(h，k)；
(2)保持抛物线y＝ax2的形状不变，将其顶点平移到(h，k)处，具体平移方法如下：

2. 平移规律
在原有函数的基础上“h值正右移，负左移；k值正上移，负下移”．概括成八个字“左加右减，上加下减”．
四、二次函数y＝ax2＋bx＋c的图象和性质

二次函数y＝ax2＋bx＋c(a，b，c为常数，a≠0)


条件
a>0
a<0
图象


开口方向
开口向上
开口向下
对称轴
直线x＝－

顶点坐标
(－，)

增减性
在对称轴的左侧，即当x<－时，y随x的增大而减小；
在对称轴的右侧，即当x>－时，y随x的增大而增大
在对称轴的左侧，即当x<－时，y随x的增大而增大；
在对称轴的右侧，即当x>－时，y随x的增大而减小
最值
当x＝－时，y有最小值为
当x＝－时，y有最大值为

　　　　　　　　　　　　　　　　　　　

,　　　　　　　　　　　　　　　
二次函数图象的变换

(2018·北部湾经济区，第9小题，3分)
将抛物线y＝x2－6x＋21向左平移2个单位后，得到新抛物线的解析式为(　　)
A．y＝(x－8)2＋5 B．y＝(x－4)2＋5
C．y＝(x－8)2＋3 D．y＝(x－4)2＋3
【思路点拨】方法一：先将解析式进行配方变为顶点式，再将顶点平移．抛物线y＝x2－6x＋21，可配方成y＝(x－6)2＋3，顶点坐标为(6，3)．因为图象向左平移2个单位，所以顶点向左平移2个单位，即新的顶点坐标变为(4，3)，而抛物线开口大小不变，于是新抛物线的解析式为y＝(x－4)2＋3.
方法二：直接运用函数图象左右平移的“左加右减”法则进行解题．向左平移2个单位，即原来解析式中所有的x都要变成(x＋2)，于是新抛物线解析式为y＝(x＋2)2－6(x＋2)＋21，整理，得y＝x2－4x＋11，配方后得y＝(x－4)2＋3.
(2020·百色，第11小题，3分)
将抛物线y ＝ ＋ 1 平移得到抛物线y＝x2＋6x＋6 ，是怎样平移得到的(　　)
A．先向左平移1个单位长度，再向上平移5个单位长度
B．先向左平移2个单位长度，再向下平移4个单位长度
C．先向右平移1个单位长度，再向上平移5个单位长度
D．先向右平移2个单位长度，再向下平移4个单位长度

,　　　　　　　　　　　　　　　二次函数的图象与性质)

(2016·玉林、防城港，第8小题，3分)
抛物线y＝x2，y＝x2，y＝－x2的共同性质是：
①都是开口向上；②都以点(0，0)为顶点；
③都以y轴为对称轴；④都关于x轴对称．
其中正确的个数有(　　)
A．1个 B．2个 C．3个 D．4个
(2017·玉林、防城港，第18小题，3分)
已知抛物线：y＝ax2＋bx＋c(a>0)经过A(－1，1)，B(2，4)两点，顶点坐标为(m，n)，有下列结论：
①b<1；②c<2；③0 则所有正确结论的序号是________．
(2020·梧州，第9小题，3分)
如图，抛物线y＝ax2＋bx＋c与直线y＝kx＋h交于A、B两点，下列是关于x的不等式或方程，结论正确的是(　　)

A．ax2＋x＋c＞h的解集是：2＜x＜4
B．ax2＋x＋c＞h的解集是：x＞4
C．ax2＋x＋c＞h的解集是：x＜2
D．ax2＋x＋c＝h的解集是：x1＝2，x2＝4
【思路点拨】ax2＋x＋c＞h 即为ax2＋bx＋c＞kx＋h，即抛物线在直线上方部分的x的取值范围，可根据图象得到ax2＋x＋c＞h的解集是x< 2或x> 4，故选项A、B、C错误；ax2＋x＋c＝h的解，即为两函数图象交点的横坐标，故选项D正确．
(2015·玉林、防城港，第12小题，3分)
如图，反比例函数y＝的图象经过二次函数y＝ax2＋bx图象的顶点(m＞0)，则有(　　)
A．a＝b＋2k
B．a＝b－2k
C．k D．a (2020·贵港，第18小题，3分)

对于抛物线y1＝－x2＋x＋1，y2＝－x2＋2x＋1，y3＝－x2＋3x＋1 ，给出以下结论：
①这三条抛物线都经过点C(0，1)；
②抛物线y3的对称轴可由抛物线y1 的对称轴向右平移一个单位而得到；
③这三条抛物线的顶点在同一条直线上；
④这三条抛物线与直线y＝1的交点中，相邻两点之间的距离相等，其中正确的结论序号是________________ .
【思路点拨】算出函数与x轴以及y＝1的交点，观察函数的对称轴.
小结
解此类题型要认真观察图象，根据题意找到图象对应对齐的x轴、y轴的部分，这一部分就是自变量x的取值范围及函数值y的取值范围.

(2020·梧州，第12小题，3分)
二次函数y＝x2－x＋a－4的图象与x轴有两个公共点，a取满足条件的最小整数，将图象在x轴上方的部分沿x轴翻折，其余部分保持不变，得到一个
新图象，当直线y＝kx－2与新图象恰有三个公共点时，则k的值不可能是(　　)
A．－1　　 B．－2
C．1 D．2



　　　　　　　　　　　　　　　　　　　
1. 在抛物线y＝－x2＋1上的一个点是(　　)
A．(1，0) B．(0，0)
C．(0，－1) D．(1，1)
2. 将抛物线y＝－x2向左平移2个单位后，得到的抛物线的解析式是(　　)
A．y＝－(x＋2)2 B．y＝－x2＋2
C．y＝－(x－2)2 D．y＝－x2－2
3. 对于函数y＝－2(x－m)2的图象，下列说法不正确的是(　　)
A．开口向下 B．对称轴是直线x＝m
C．最大值为0 D．与y轴不相交
4. 抛物线y＝ax2＋bx－3过点(2，4)，则代数式8a＋4b＋1的值为(　　)
A．－2 B．2
C．15 D．－15

5. 如图，已知抛物线y＝x2＋bx＋c的对称轴为x＝2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为(0，3)，则点B的坐标为(　　)
A．(2，3) B．(3，2)
C．(3，3) D．(4，3)
6. 如图是二次函数y＝ax2＋bx＋c的部分图象，由图象可知不等式ax2＋bx＋c<0的解集是(　　)

A．－1 B．x>5
C．x<－1且x>5
D．x<－1或x>5
7. (2020·玉林) 把二次函数y＝ax2＋bx＋c(a>0)的图象作关于x轴的对称变换，所得图象的解析式为y＝－a(x－1)2＋4a，若a＋b＋c≤0，则m的最大值为(　　)
A．－4 　　 B．0 C．2 D．6
8. 抛物线y＝－2x2＋1的对称轴是________．
9. 抛物线y＝(x－1)2＋2的顶点坐标是________．
10. 已知二次函数y＝－2x2－2x＋3的图象上有两点A(－7，y1)，B(－8，y2)，则y1________y2.(选填“>”“<”或“＝”)．
11. 函数y＝x2＋mx－4，当x<2时，y随x的增大而减小，则m的取值范围是________．
12. 把二次函数y＝(x－1)2＋2的图象绕原点旋转180°后得到的图象的解析式为__________________．
13. 抛物线y＝x2－4x＋与x轴的一个交点的坐标为，则此抛物线与x轴的另一个交点的坐标是________．


14. 如图，已知⊙P的半径为2，圆心P在抛物线y＝x2－1上运动，当⊙P与x轴相切时，圆心P的坐标为____________．
15. 如图，已知二次函数y＝－x2＋bx＋c的图象经过A(2，0)，B(0，－6)两点．
(1)求这个二次函数的解析式；
(2)设该二次函数图象的对称轴与x轴交于点C，连接BA，BC，求△ABC的面积．











16. 如图，抛物线y＝－x2＋bx＋c与x轴交于A，B两点，与y轴交于点C，且OA＝2，OC＝3.
(1)求抛物线的解析式；
(2)若点D(2，2)是抛物线上一点，那么在抛物线的对称轴上，是否存在一点P，使得△BDP的周长最小，若存在，请求出点P的坐标，若不存在，请说明理由．
(注：二次函数y＝ax2＋bx＋c(a≠0)的对称轴是直线x＝－)






第2课时


一、抛物线y＝ax2＋bx＋c中a，b，c的作用
1．a决定开口方向及开口大小，这与y＝ax2中的a完全一样．
2．b和a共同决定抛物线对称轴的位置．由于抛物线y＝ax2＋bx＋c的对称轴是直线x＝－，故：
(1)b＝0时，对称轴为y轴；
(2)>0(即a，b同号)时，对称轴在y轴左侧；
(3)<0(即a，b异号)时，对称轴在y轴右侧．
3．c的大小决定抛物线y＝ax2＋bx＋c与y轴交点的位置．当x＝0时，y＝c，所以抛物线y＝ax2＋bx＋c与y轴有且只有一个交点(0，c)：
(1)c＝0，抛物线经过原点；
(2)c>0，与y轴交于正半轴；
(3)c<0，与y轴交于负半轴．
以上三点中，当结论和条件互换时，仍成立．如抛物线的对称轴在y轴右侧，则<0.
二、用待定系数法求二次函数的解析式
1．一般式：y＝ax2＋bx＋c(a≠0)．已知图象上三点或三对x，y的值，通常选择一般式．
2．顶点式：y＝a(x－h)2＋k(a≠0)．已知图象的顶点或对称轴，通常选择顶点式．
3．交点式：已知图象与x轴的交点横坐标x1，x2，通常选用交点式：y＝a(x－x1)(x－x2)(a≠0)．

三、直线与抛物线的交点
1．y轴与抛物线y＝ax2＋bx＋c的交点为(0，c)．
2．与y轴平行的直线x＝h与抛物线y＝ax2＋bx＋c有且只有一个交点(h，ah2＋bh＋c)．
3．抛物线与x轴的交点：二次函数y＝ax2＋bx＋c的图象与x轴的两个交点的横坐标x1，x2是对应一元二次方程ax2＋bx＋c＝0(a≠0)的两个实数根．抛物线与x轴的交点情况可以由对应的一元二次方程的根的判别式判定：
①有两个交点⇔Δ>0⇔抛物线与x轴相交；
②有一个交点(顶点在x轴上)⇔Δ＝0⇔抛物线与x轴相切；
③没有交点⇔Δ<0⇔抛物线与x轴相离．
4．平行于x轴的直线与抛物线的交点同样可能有0个交点、1个交点、2个交点．当有2个交点时，两交点的纵坐标相等，设纵坐标为k，则横坐标是ax2＋bx＋c＝k(a≠0)的两个实数根．
5．一次函数y＝kx＋n(k≠0)的图象l与二次函数y＝ax2＋bx＋c(a≠0)的图象G的交点，由方程组的解的数目来确定：
(1)方程组有两组不同的解时⇔l与G有两个交点；
(2)方程组只有一组解时⇔l与G只有一个交点；(3)方程组无解时⇔l与G没有交点．
6．抛物线与x轴两交点之间的距离：若抛物线y＝ax2＋bx＋c(a≠0)与x轴两交点为A(x1，0)，B(x2，0)，AB＝.

　　　　　　　　　　　　　　　　　　　

,　　　　　　　　　　　　　　　
用待定系数法求二次函数的解析式

求满足下列条件的函数解析式：
(1)已知抛物线经过点(1，3)，(－1，1)，(0，－1)；
(2)已知抛物线的对称轴是直线x＝1，且经过点(3，4)，与y轴的交点是(0，1)；
(3)已知抛物线经过点(1，0)，(－3，0)，(0，6)．
【思路点拨】一般地，求二次函数的解析式时，已知三点(不是与x轴的交点)，用一般式；已知对称轴或顶点坐标，用顶点式；已知与x轴的两个交点，用交点式．

经过A(4，0)，B(－2，0)，C(0，3)三点的抛物线解析式是__________．
,　　　　　　　　　　　　　　　
二次函数与一元二次方程的关系
(2014·柳州，第11小题，3分)小兰画了一个函数y＝x2＋ax＋b的图象如图，则关于x的方程x2＋ax＋b＝0的解是(　　)


A．无解
B．x＝1
C．x＝－4
D．x＝－1或x＝4
【思路点拨】关于x的方程x2＋ax＋b＝0的解是抛物线y＝x2＋ax＋b与x轴交点的横坐标．如图，∵函数y＝x2＋ax＋b的图象与x轴交点坐标分别是(－1，0)，(4，0)，∴关于x的方程x2＋ax＋b＝0的解是x＝－1或x＝4.
(2016·南宁，第12小题，3分)二次函数y＝ax2＋bx＋c(a≠0) 和正比例函数y＝x的图象如图所示，则方程 ax2＋x＋c＝0(a≠0)的两根之和(　　)

A．大于0
B．等于0
C．小于0
D．不能确定

,　　　　　　　　　　　　　　　
二次函数图象与系数的关系


(2019·河池，第11小题，3分)如图，抛物线y＝ax2＋bx＋c的对称轴为直线x＝1，则下列结论中，错误的是(　　)
A．ac<0 B．b2－4ac>0
C．2a－b＝0 D．a－b＋c＝0
小结
二次函数图象与系数的关系，常见的解题方法如下：①由抛物线开口方向确定a；②由对称轴位置确定b，ab；③由抛物线与y轴的交点位置确定c；④由抛物线与x轴的交点的个数确定b2－4ac；⑤由对称轴x＝±1确定2a±b；⑥根据特殊点确定由a，b，c组成的式子，如x＝1，根据图象可确定a＋b＋c与0 的关系，x＝－1，根据图象可确定a－b＋c与0 的关系，同理可判断x＝2，x＝－2，x＝3，x＝－3时相关的式子与0的关系.


(2017·贺州，第17小题，3分)二次函数y＝ax2＋bx＋c(a，b，c为常数，a≠0)的图象如图所示，下列结论：
①abc＜0；②2a＋b＜0；③b2－4ac＝0；④8a＋c＜0；⑤a∶b∶c＝(－1)∶2∶3，其中正确的结论有________．



1. 抛物线y＝－3x2－x＋4与坐标轴的交点个数是(　　)
A．3个 B．2个 C．1个 D．0个
2. 关于抛物线y＝－x2＋2x－3，下列结论正确的是(　　)
A．与x轴有两个交点
B．开口向上
C．与y轴的交点坐标是(0，3)
D．顶点坐标是(1，－2)
3. 如图，函数y＝－x2＋bx＋c的部分图象与x轴、y轴的交点分别为A(1，0)，B(0，3)，对称轴是x＝－1.在下列结论中，错误的是(　　)

A．顶点坐标为(－1，4)
B．函数的解析式为y＝－x2－2x＋3
C．当x<0时，y随x的增大而增大
D．抛物线与x轴的另一个交点是(－3，0)
4. (2020·眉山)已知二次函数y＝x2－2ax＋a2－2a－4(a为常数)的图象与x轴有交点，且当x＞3时，y随x的增大而增大，则a的取值范围是( D )
A．a≥－2 B．a＜3
C．－2≤a＜3 D．－2≤a≤3
5. (2020·杭州)设函数y＝a(x－h)2＋k(a，h，k是实数，a≠0)，当x＝1时，y＝1；当x＝8时，y＝8，( C )
A．若h＝4，则a＜0 B．若h＝5，则a＞0
C．若h＝6，则a＜0 D．若h＝7，则a＞0
6. (2020·嘉兴)已知二次函数y＝x2，当a≤x≤b时，m≤y≤n，则下列说法正确的是( B )
A．当n－m＝1时，b－a有最小值
B．当n－m＝1时，b－a有最大值
C．当b－a＝1时，n－m无最小值
D．当b－a＝1时，n－m有最大值
7. (2020·黔西南州)如图，抛物线y＝ax2＋bx＋4交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C，D两点(点C在点D右边)，对称轴为直线x＝，连接AC，AD，BC.若点B关于直线AC的对称点恰好落在线段OC上，下列结论中错误的是( D )

A．点B坐标为(5，4)
B．AB＝AD
C．a＝－
D．OC·OD＝16


8. 如图，垂直于x轴的直线AB分别与抛物线C1：y＝x2(x≥0)和抛物线C2：y＝(x≥0)交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E，F，则的值为(　　)
A. B. C. D.
9. 抛物线y＝ax2＋bx＋c(a≠0)的顶点是A(2，1)，且经过点B(1，0)，则抛物线的函数关系式为________________________________________________________________________．
10. 将y＝2x2的函数图象向左平移2个单位长度后，得到的函数解析式是________．
11. 若抛物线y＝ax2＋bx＋c经过点(－1，10)，则a－b＋c＝________.
12. 某同学利用描点法画二次函数y＝ax2＋bx＋c(a≠0)的图象时，列出的部分数据如下表：
x
0
1
2
3
4
y
3
0
－2
0
3
　　经检查，发现表格中恰好有一组数据计算错误，请你根据上述信息写出该二次函数的解析式：________________________.
13. (2020·无锡)二次函数y＝ax2－3ax＋3的图象过点A(6，0)，且与y轴交于点B，点M在该抛物线的对称轴上，若△ABM是以AB为直角边的直角三角形，则点M的坐标为________________．
14. 如图，二次函数y＝ax2－4x＋c的图象经过坐标原点，与x轴交于点A.
(1)求此二次函数的解析式；
(2)在抛物线上存在点P，满足S△AOP＝8，请直接写出点P的坐标．

















15. 已知：如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴相交于两点A(1，0)，B(3，0)，与y轴相交于点C(0，3)．
(1)求抛物线的函数关系式；
(2)若点D(，m)是抛物线y＝ax2＋bx＋c上的一点，请求出m的值，并求出此时△ABD的面积．













16．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，－4)，O(0，0)，B(2，0)三点．
(1)求抛物线y＝ax2＋bx＋c的解析式；
(2)若点M是该抛物线对称轴上的一点，求AM＋OM的最小值．











17. (2020·杭州)在平面直角坐标系中，设二次函数y1＝x2＋bx＋a，y2＝ax2＋bx＋1(a，b是实数，a≠0)．
(1)若函数y1的对称轴为直线x＝3，且函数y1的图象经过点(a，b)，求函数y1的表达式；
(2)若函数y1的图象经过点(r，0)，其中r≠0，求证：函数y2的图象经过点(，0)；
(3)设函数y1和函数y2的最小值分别为m和n，若m＋n＝0，求m，n的值．

第3课时

一、二次函数的应用
1. 二次函数常用来解决最优化问题，这类问题实际上就是求函数的最大(小)值．
2. 二次函数的应用包括以下方面：分析和表示不同背景下实际问题中变量之间的二次函数关系；运用二次函数的知识解决实际问题中的最大(小)值问题．
3. 解决实际问题时的基本思路：(1)理解问题；(2)分析问题中的变量和常量；(3)用函数表达式表示出它们之间的关系；(4)利用二次函数的有关性质进行求解；(5)检验结果的合理性，对问题加以拓展等．
二、与二次函数有关的综合题
二次函数综合题，一般涉及待定系数法求函数解析式、抛物线的对称轴、顶点坐标；图形平移、对称、旋转的性质；等腰三角形、平行四边形、矩形、菱形、正方形、圆等特殊图形的性质；转化思想、分类讨论思想、数形结合思想、方程思想等多种数学思想．

　　　　　　　　　　　　　　　　　　　
,　　　　　　　　　　　　　　　
二次函数的实际应用

(2015·玉林、防城港，第24小题，9分)某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系，如图所示．

(1)求y关于x的函数关系式(不要求写出x的取值范围)；
(2)应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？
【思路点拨】(1)认真观察图象，把点(20，20)，(30，0)分别代入y＝kx＋b建立方程组即可求出k，b的值，从而得出y关于x的函数关系式．(2)求出利润与销售价x之间的函数关系式，再根据相关函数的性质确定最大利润．

小结
应用二次函数解决实际问题中的最优化问题，实际上就是求函数的最大(小)值．解题时要先根据题目提供的条件，确定函数关系式，再根据二次函数的性质确定最大(小)值，从而确定最优方案.
(2019·梧州，第24小题，10分)我市某超市销售一种文具，进价为5元/件．售价为6元/件时，当天的销售量为100件．在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件．设当天销售单价统一为x元/件(x≥6，且x是按0.5元的倍数上涨)，当天销售利润为y元．
(1)求y与x的函数关系式(不要求写出自变量的取值范围)；
(2)要使当天销售利润不低于240元，求当天销售单价所在的范围；
(3)若每件文具的利润不超过80%，要想当天获得利润最大，每件文具售价为多少元？并求出最大利润．











,　　　　　　　　　　　　　　　
与二次函数有关的综合题

(2020·贵港，第25小题，11分) 如图，已知抛物线y＝x2＋bx＋c与x轴相交于A(－6，0)，B(1，0)两点，与y轴相交于点C，直线l⊥AC，垂足为C.
(1)求该抛物线的表达式；
(2)若直线l与该抛物线的另一个交点为D，求D的坐标；
(3)设动点P(m，n)在该抛物线上，当∠PAC＝45°时，求m的值 .
【思路点拨】(1)将A、B两点带进去即可求得b、c的值；(2)利用三角形相似求出l的解析式，进而联立方程组求出交点的横坐标；(3)分类讨论点P的位置，通过求AP延长线于l的交点坐标，进而得到AP所在直线的解析式为解题突破口 .




小结
在几何图形中建立函数关系式，体现了数形结合的数学思想，要注意运用图形的有关性质或公式(如相似、几何图形面积等)建立有关关系式，从而将几何问题转化为代数问题.
(2020·玉林，第26小题，12分)
已知抛物线y1＝－x2－2x＋3与x轴交于A，B两点(A在B的左侧)，与y轴交于点C.
(1)直接写出点A，B，C的坐标；
(2)将抛物线y1经过向右和向下平移，使得到的抛物线y2与x轴交于B, B′两点(B′在B的右侧)，顶点D的对应点D′，若∠BD′B′＝90°，求点B′的坐标及抛物线y2的解析式；
(3)在(2)的条件下，若点Q在x轴上，则在抛物线y1或y2上是否存在点P，使以B′，C，Q，P为顶点的四边形是平行四边形？如果存在，求出所有符合条件的点P的坐标；如果不存在，请说明理由．


　　　　　　　　　　　　　　　　　　　


1. 如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千．拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为________米．

2. 如图，从地面竖直向上抛出一个小球，小球的高度h(单位：m)与小球运动时间t(单位：s)之间的关系式为h＝30t－5t2，那么小球从抛出至回落到地面所需要的时间是________s.
3. 某种火箭被竖直向上发射时，它的高度h(m)与时间t(s)的关系可以用公式h＝－5t2＋150t＋10表示．经过________s，火箭达到它的最高点．
4. 向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y＝ax2＋bx＋c(a≠0)．若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是(　　)
A．第8秒 B．第10秒
C．第12秒 D．第15秒
5. (2019·无锡)某宾馆共有80间客房．宾馆负责人根据经验作出预测：今年7月份，每天的房间空闲数y(间)与定价x(元/间)之间满足y＝x－42(x≥168)．若宾馆每天的日常运营成本为5 000元，有客人入住的房间，宾馆每天每间另外还需支出28元的各种费用，宾馆想要获得最大利润，同时也想让客人得到实惠，应将房间定价确定为( B )
A．252元/间 B．256元/间
C．258元/间 D．260元/间
6. (2020·贺州) 某学生在一平地上推铅球，铅球出手时离地面的高度为米，出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为y＝－x2＋bx＋c ，当铅球运行至与出手高度相等时，与出手点水平距离为8米，则该学生推铅球的成绩为________ 米 .
7. (2020·广州)对某条线段的长度进行了3次测量，得到3个结果(单位：mm)：9.9，10.1，10.0，若用a作为这条线段长度的近似值，当a＝________mm时，(a－9.9)2＋(a－10.1)2＋(a－10.0)2最小．对另一条线段的长度进行了n次测量，得到n个结果(单位：mm)：x1，x2，…，xn，若用x作为这条线段长度的近似值，当x＝________________mm时，(x－x1)2＋(x－x2)2＋…＋(x－xn)2最小．
8. 某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙(墙足够长)，已知计划中的建筑材料可建围墙的总长为50 m．设饲养室长为x(单位：m)，占地面积为y(单位：m2)．
(1)如图1，问饲养室长x为多少时，占地面积y最大？
(2)如图2，现要求在图中所示位置留2 m宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比(1)中的长多2 m就行了．”请你通过计算，判断小敏的说法是否正确．
　










9. 某商场以每件50元的价格购进一种商品，销售中发现这种商品每天的销售量m(件)与每件的销售价格x(元)满足一次函数，其图象如图所示．
(1)每天的销售数量m(件)与每件的销售价格x(元)的函数解析式是________________________________________________________________________；
(2)求该商场每天销售这种商品的销售利润y(元)与每件的销售价格x(元)之间的函数解析式；
(3)每件商品的销售价格在什么范围内，每天的销售利润随着销售价格的提高而增加？












10. 某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价每天增加x元(x为10的正整数倍)．
(1)设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；
(2)设宾馆一天的利润为w元，求w与x的函数关系式；
(3)一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？










11. 用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)．
设竖档AB＝x米，请根据以下图案回答下列问题：(题中的不锈钢材料总长度均指各图中所有黑线的长度和，所有横档和竖档分别与AD，AB平行)

(1)在图①中，如果不锈钢材料总长度为12米，当x为多少时，矩形框架ABCD的面积为3平方米？
(2)在图②中，如果不锈钢材料总长度为12米，当x为多少时，矩形框架ABCD的面积S最大？最大面积是多少？
(3)在图③中，如果不锈钢材料总长度为a米，共有n条竖档，那么当x为多少时，矩形框架ABCD的面积S最大？最大面积是多少？










12. 如图，在平面直角坐标系中，△ABC为等腰直角三角形，∠ACB＝90°，抛物线y＝－x2＋bx＋c经过A，B两点，其中点A，C的坐标分别为(1，0)，(－4，0)，抛物线的顶点为点D.
(1)求抛物线的解析式；
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A，B重合)，过点E作x轴的垂线，交抛物线于点F，当线段FE的长度最大时，求点E的坐标；
(3)在(2)的条件下，抛物线上是否存在一点P，使△PEF是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．


























13. 如图，已知抛物线经过A(－2，0)，B(－3，3)及原点O，顶点为C.
(1)求抛物线的解析式；
(2)若点D在抛物线上，点E在抛物线的对称轴上，且以A，O，D，E为顶点的四边形是平行四边形，求点D的坐标；
(3)P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．







































14. 已知一元二次方程x2－4x＋3＝0的两根是m，n，且m (1)求抛物线的解析式；
(2)若(1)中的抛物线与x轴的另一个交点为C.根据图象回答，当x取何值时，抛物线的图象在直线BC的上方？
(3)点P在线段OC上，作PE⊥x轴与抛物线交于点E，若直线BC将△CPE的面积分成相等的两部分，求点P的坐标．






第16讲　二次函数
第1课时
【基础梳理】
一、y＝ax2＋bx＋c　≠0　二、1.顶点　三、抛物线　y
【重点突破】
[例1]D　[变式1]B　[例2]B　[变式2]①②④　
[例3]D　[变式3]D　[例4]①②④　[变式4]D
【达标检测】
1．A　2.A　3.D　4.C　5.D　6.D　7.D　
8．y轴　9.(1，2)　10.>　11.m≤－4　
12．y＝－(x＋1)2－2　13.(3，0)　
14．(，2)或(－，2)
15．解：(1)把A(2，0)，B(0，－6)代入y＝－x2＋bx＋c，
得解得
∴这个二次函数的解析式为y＝－x2＋4x－6.
(2)∵该抛物线对称轴为直线x＝－＝4，
∴点C的坐标为(4，0)．
∴AC＝OC－OA＝4－2＝2.
∴S△ABC＝AC·OB＝×2×6＝6.
16．解：(1)由已知条件得A(－2，0)，C(0，3)，将A(－2，0)，C(0，3)代入y＝－x2＋bx＋c，得
解得
∴此二次函数的解析式为y＝－x2＋x＋3.
(2)如图，连接AD交对称轴于点P，则P为所求的点，设直线AD解析式为y＝kx＋b，

由已知得
解得
∴直线AD解析式为y＝x＋1.
对称轴为直线：x＝－＝，当x＝时，y＝，
∴P.
第2课时
【重点突破】
[例1]解：(1)设抛物线的解析式为y＝ax2＋bx＋c.
由题意，得解得
所以抛物线的解析式为y＝3x2＋x－1.
(2)设抛物线的解析式为y＝a(x－1)2＋b.
由抛物线经过点(3，4)，(0，1)，可得
解得a＝1，b＝0.因此，抛物线的解析式为y＝(x－1)2.
(3)设抛物线的解析式为y＝a(x－1)(x＋3)．
由抛物线经过点(0，6)，可得
6＝a(0－1)(0＋3)．解得a＝－2.
因此，抛物线的解析式为y＝－2(x－1)(x＋3)．
[变式1]y＝－x2＋x＋3
[例2]D　[变式2]A　[例3]C　[变式3]①④⑤
【达标检测】
1．A　2.D　3.C　4.D　5.C　6.B　7.D　8.D　
9．y＝－x2＋4x－3　10.y＝2(x＋2)2　11. 10　
12．y＝x2－4x＋3　13.或
14．解：(1)由已知条件得
解得
∴此二次函数的解析式为y＝－x2－4x.
(2)点P的坐标是：(－2，4)或(－2＋2，－4)或
(－2－2，－4)．
15．解：(1)由已知得　解得
∴y＝x2－4x＋3.
(2)把D代入y＝x2－4x＋3，得m＝，
∴S△ABD＝×2×＝.
16．解：(1)把A(－2，－4)，O(0，0)，B(2，0)代入y＝ax2＋bx＋c，
得解这个方程组，得
所以解析式为y＝－x2＋x.
(2)由y＝－x2＋x＝－(x－1)2＋可得，抛物线的对称轴为x＝1，并且对称轴垂直平分线段OB，
∴OM＝BM.

∴AM＋OM＝AM＋BM.
连接AB交直线x＝1于M点，
则此时AM＋OM最小．
过点A作AN⊥x轴于点N，
在Rt△ABN中，
AB＝＝＝4，
因此AM＋OM最小值为4.
17．(1)解：由题意，得到－＝3，
解得b＝－6，
∵函数y1的图象经过点(a，b)，
∴a2－6a＋a＝－6，解得a＝2或a＝3.
∴函数y1＝x2－6x＋2或y1＝x2－6x＋3.
(2)证明：∵函数y1的图象经过点(r，0)，
∴r2＋br＋a＝0.
∵r≠0，两边同除以r2，得1＋＋＝0，
即a2＋b·＋1＝0，
∴是方程ax2＋bx＋1＝0的一个实数根，
即函数y2的图象经过点.
(3)由题意，得a＞0，∴m＝，n＝.
∵m＋n＝0，∴＋＝0.
∴(4a－b2)(a＋1)＝0.
∵a＋1≠0，∴4a－b2＝0.
∴m＝0，n＝0.
第3课时
【重点突破】
[例1]解：(1)设y与x的函数解析式为y＝kx＋b，
将(20，20)，(30，0)两点代入，得
解得
∴y关于x的函数关系式是y＝－2x＋60.

(2)设每天的利润为w元，则
w＝(x－10)y＝(x－10)(－2x＋60)＝－2x2＋80x－600＝－2(x－20)2＋200，
∴当x＝20时，w取得最大值．
∴当销售价定为20元/千克时，每天销售利润最大为200元．
[变式1]解：(1)依题意，得y＝(x－5)＝－10x2＋210x－800.
(2)依题意y＝－10x2＋210x－800≥240.解得8≤x≤13.
(3)由≤80%，解得x≤9.又∵x≥6，∴6≤x≤9.
由(1)得y＝－10x2＋210x－800＝－10＋
∴当6≤x≤9时，y随着x的增大而增大．
∴当x＝9时，y取得最大值， y最大＝280.
即每件文具售价为9元时，最大利润为280元．
[例2]解：(1)由题可得抛物线的表达式是
y＝＝x2＋－3；
(2)由(1)可得C(0，3)，∵A(－6，0)，
设直线AC的解析式为y＝kx＋n，
则解得
∴直线AC的解析式是y＝－x－3.
如解图①，设直线l与x轴的交点为K，

图①
∵直线l⊥AC，
∴易得△OCK∽△OAC，
∴＝，即＝，
解得OK＝，∴K.
∴直线l的解析式是y＝2x－3.
联立得
x2＋x＝0，解得x1＝0(与C点重合舍去)，x2＝－1.
∴D(－1，－5)；
(3)①当点P在直线AC上方的抛物线上时，如解图②，延长AP交直线l于点M，作MN⊥y轴于点N，
∵l⊥AC，∠PAC＝45°，

图②

∴△MAC是等腰直角三角形．
∴AC＝CM.
∵∠AOC＝∠CNM＝∠ACM＝90°.
∴∠ACO＝∠CMN.
∴△ACO≌△CMN.
∴MN＝OC＝3，CN＝AO＝6.
∴ON＝3.
∴点M坐标为(3，3)．
∴直线AM的解析式是y＝x＋2.
联立
得3x2＋13x－30＝0，解得x1＝－6(舍去)，x2＝.
当x＝时，y＝x＋2＝，
∴点P的坐标是(， )；

图③
②当点P位于直线AC下方的抛物线上时，如解图③，作点M关于点C的对称点F，连接AF交抛物线于点P，根据点的平移可得出点F坐标是(－3，－3－6)，即(－3，－9)．
易得经过点A与点F的直线解析式是y＝－3x－18，
联立
解得x3＝－6(舍去)，x4＝－5.
当x＝－5时，y＝－3×－18＝－3，
∴点P的坐标是(－5，－3)，
综上所述，m的值为或－5.
[变式2]解：(1)A(－3，0)，B(1，0)，C(0，3)．
(2)∵∠BD′B′＝90°，D′是抛物线y2的顶点，
∴BD′＝B′D′，即∠D′B′B＝45°.
∴OB′＝OC＝3.∴B′(3，0)．
∵抛物线y2是抛物线y1平移得到，
∴设抛物线y2的解析式为y2＝－，
将B(1，0)与B′(3，0)代入，得
y2＝－＝－x2＋4x－3.
(3)存在．
∵点P、Q的位置未知，∴需分两种情况讨论：
①当B′C为平行四边形的边时，
∵点C(0，3)，B′(3，0)，且点Q在x轴上，
∴当PC∥x轴时，
令y1＝3，解得x1＝－2，x2＝0(舍去)，
∴点P的坐标为(－2，3)；
同理，直线y＝－3与抛物线的交点即为P.
令y1＝－3，解得x1＝－1－，x2＝－1＋，
∴P坐标是(－1－，－3)或(－1＋，－3)；
令y2＝－3，解得x1＝0，x2＝4，
∴点P的坐标是(0，－3)或(4，－3)．
②当B′C为平行四边形的对角线时，
∵四边形B′QCP是平行四边形，
∴CP∥B′Q，所以点P的坐标为(－2，3)；
除此之外，无法构成满足条件的平行四边形．
综上所述，存在点P，使得以B′，C，Q，P为顶点的四边形是平行四边形，点P的坐标分别是(－2，3)或(－1－，－3)或(－1＋，－3)或(0，－3)或(4，－3)．
【达标检测】
1．0.5　2. 6　3. 15　4.B　5.B　6.10　
7．10.0　
8．解：(1)∵y＝x·＝－(x－25)2＋，
∴当x＝25时，占地面积y最大．
即当饲养室长为25 m时，占地面积最大．
(2)∵y＝x·＝－(x－26)2＋338，
∴当x＝26时，占地面积y最大．
即当饲养室长为26 m时，占地面积最大．
∵26－25＝1≠2，∴小敏的说法不正确．
9．(1)m＝－x＋100(0≤x≤100)
(2)每件商品的利润为x－50，所以每天的利润为：
y＝(x－50)(－x＋100)，
∴函数解析式为y＝－x2＋150x－5 000.
(3)∵x＝－＝75，∴在50＜x＜75元时，每天的销售利润随着x的增大而增大．
10．解：(1)y＝50－x(0≤x≤160，且x是10的整数倍)．
(2)w＝(180＋x－20)＝－x2＋34x＋8000.
(3)w＝－x2＋34x＋8 000＝－(x－170)2＋10890，
当x＜170时，w随x增大而增大，但0≤x≤160，
∴当x＝160时，w最大＝10 880.
当x＝160时，y＝50－x＝34.答：(略)
11．解：(1)由题意，BC的长为(4－x)米，依题意得
x(4－x)＝3，即x2－4x＋3＝0.
解得x1＝1，x2＝3.即当AB的长度为1米或3米时，矩形框架ABCD的面积为3平方米．
(2)S＝x＝－x2＋4x＝－＋3.
∴当x＝时，S有最大值3.
即当x为时，矩形框架ABCD的面积S最大，最大面积是3平方米．
(3)S＝x·＝－x2＋x＝－＋.
∵－＜0，∴当x＝时，矩形框架ABCD的面积S最大，最大面积是平方米．
12．解：(1)由已知，可得A(1，0)，B(－4，－5)．
二次函数y＝－x2＋bx＋c的图象经过点A(1，0)，B(－4，－5)，有解得
∴抛物线的解析式为y＝－x2－2x＋3.
(2)如图1，设直线AB解析式为y＝kx＋b，
∵直线AB经过点A(1，0)，B(－4，－5)，

图1
解得
∴直线AB的解析式为y＝x－1.
设点E的坐标为(t，t－1)，
∵点F在抛物线上，且EF⊥x轴，
设点F的坐标为(t，－t2－2t＋3)
∴FE＝－t2－2t＋3－(t－1)
＝－t2－3t＋4
＝－＋.
∴当t＝－时，FE取最大值，
此时，点E的坐标为.

图2
(3)存在点P，能使△PEF是以EF为直角边的直角三角形，理由如下：
①如图2，过点E作直线a⊥EF交抛物线于点P.
设点P(m，－m2－2m＋3)，
由(2)可知E，
则有－m2－2m＋3＝－.
解得m1＝－1＋，m2＝－1－.
∴P1，P2.
②如图2，过点F作直线b⊥EF，交抛物线于点P3.
设P3(n，－n2－2n＋3)，
由(2)可知点F，
则有－n2－2n＋3＝.解得n1＝－，n2＝－.
∴P3，P4(舍去)．
综上所述，符合条件的点P的坐标有：
P1，P2，P3，
能使△PEF是以EF为直角边的直角三角形．
13．解：(1)∵抛物线过原点O，
∴可设抛物线的解析式为y＝ax2＋bx.
将A(－2，0)，B(－3，3)代入，得解得
∴抛物线的解析式为y＝x2＋2x.
(2)①当AO为边时，
∵以A，O，D，E为顶点的四边形是平行四边形．
∴DE∥AO，且DE＝AO＝2.
∵点E在对称轴x＝－1上，
∴点D的横坐标为1或－3.即符合条件的点D有两个，
分别记为D1，D2.而当x＝1时，y＝3；
当x＝－3时，y＝3.
∴D1(1，3)，D2(－3，3)．
②当AO为对角线时，则DE与AO互相平分．又点E在对称轴上，且线段AO的中点横坐标为－1，由对称性知，符合条件的点D只有一个，即顶点C(－1，－1)．
综上所述，符合条件的点D共有三个，分别为D1(1，3)，D2(－3，3)，C(－1，－1)．
(3)存在．∵B(－3，3)，C(－1，－1)，根据勾股定理得
BO2＝18，CO2＝2，BC2＝20.
∴BO2＋CO2＝BC2.∴△BOC是直角三角形．
假设存在点P，使得以P，M，A为顶点的三角形与Rt△BOC相似．
设P(x，y)，由题意知x＞0，y＞0，且y＝x2＋2x.
①若△AMP∽△BOC，则＝.则＝，
即x＋2＝3(x2＋2x)．解得x1＝，x2＝－2(舍去)．
当x＝时，y＝，即P.
②若△PMA∽△BOC，则＝.则＝，
即x2＋2x＝3(x＋2)，
解得x1＝3，x2＝－2(舍去)．
当x＝3时，y＝15，即P(3，15)．
综上所述，符合条件的点P有两个，分别是
P1，P2(3，15)．

14．解：(1)∵x2－4x＋3＝0的两个根为x1＝1，x2＝3.
∴A点坐标为(1，0)，B点坐标为(0，3)．
又∵抛物线y＝－x2＋bx＋c的图象经过点A(1，0)，B(0，3)，
∴解得
∴抛物线的解析式为y＝－x2－2x＋3.
(2)作直线BC，由①得y＝－x2－2x＋3.
∵抛物线y＝－x2－2x＋3与x轴的另一交点为C，
令－x2－2x＋3＝0.解得：x1＝1，x2＝－3.
∴C点坐标为(－3，0)．
由图可知：当－3＜x＜0时，抛物线的图象在直线BC的上方．
(3)设直线BC交PE于F，P点坐标为(a，0)，则E点坐标为(a，－a2－2a＋3)．
∵直线BC将△CPE的面积分成相等的两部分，
∴F是线段PE的中点．即F点坐标是.
∵直线BC过点B(0，3)和点C(－3，0)，易得直线BC的解析式为y＝x＋3.
∵点F在直线BC上，∴＝a＋3.
解得a1＝－1，a2＝－3(此时点P与点C重合，舍去)，
∴P点的坐标是(－1，0)．