中考数学全程复习方略 微专题四 中点四边形 课件

这是一份中考数学全程复习方略 微专题四 中点四边形 课件，共19页。PPT课件主要包含了主干必备，平行四边形，正方形等内容，欢迎下载使用。

【微点警示】1.中点四边形的证明:中点四边形只与原四边形的对角线有关,其证明运用了三角形的中位线定理.
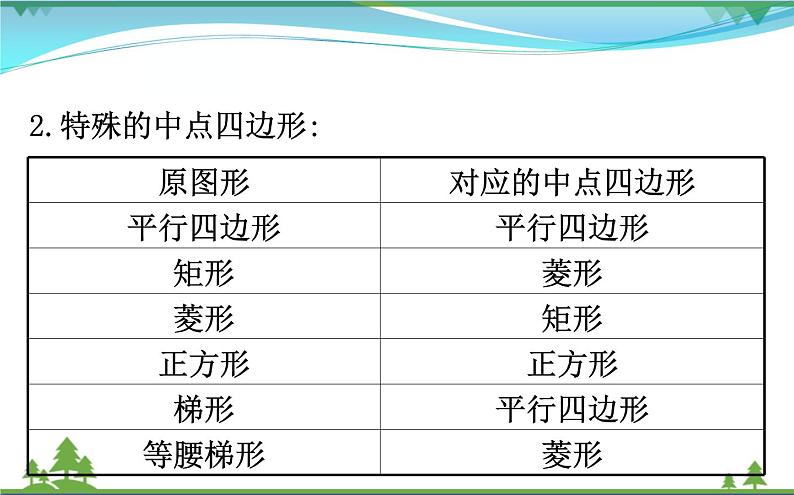
2.特殊的中点四边形:
3.中点四边形的周长:是原四边形两条对角线之和的长度,不是原四边形周长的一半.4.中点四边形的面积:是原图形的一半
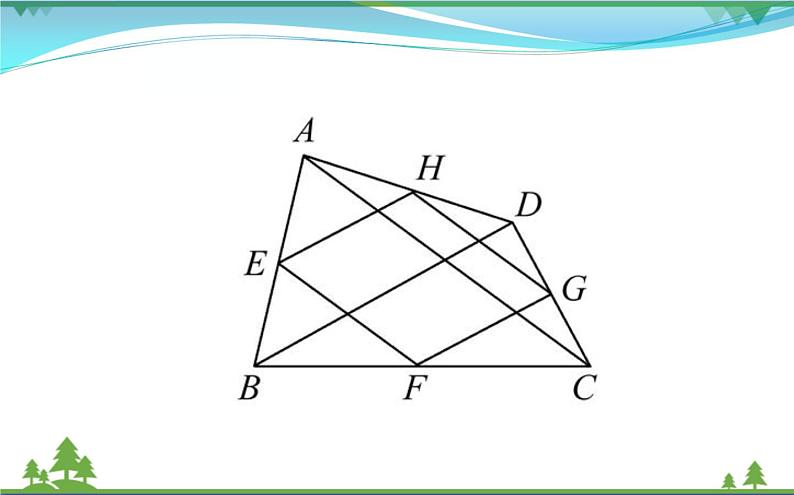
【核心突破】【类型一】确定中点四边形的形状例1(2018·临沂中考)如图,点E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是(　 　)A.1　　　B.2　　　C.3　　　D.4
【类型二】进行中点四边形的计算 例2(2018·陕西中考)如图,在菱形ABCD中.点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE.若EH=2EF,则下列结论正确的是(　 　)
A.AB= EF　　　　　　　B.AB=2EFC.AB= EFD.AB= EF
【明·技法】充分利用对角线解决中点四边形问题(1)确定中点四边形的形状,要先画出对角线,根据两条对角线的大小和位置判断.(2)进行中点四边形的计算,要先画出对角线,根据三角形的中位线定理解答.
【题组过关】1.(2019·株洲模拟)如图,点E,F,G,H分别为四边形ABCD的四边AB,BC,CD,DA的中点,则关于四边形EFGH,下列说法正确的为(　 　)
A.一定不是平行四边形　B.一定不是中心对称图形C.可能是轴对称图形D.当AC=BD时它是矩形
2.(2019·呼和浩特模拟)如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为_______. 
3.(2019·荆门模拟)如图,点E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论.(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)