数学6.4 平面向量的应用优质ppt课件

这是一份数学6.4 平面向量的应用优质ppt课件，共33页。PPT课件主要包含了探究一，探究二，探究三，探究四，思维辨析，随堂演练，答案B等内容，欢迎下载使用。

　一、正弦定理1.思考
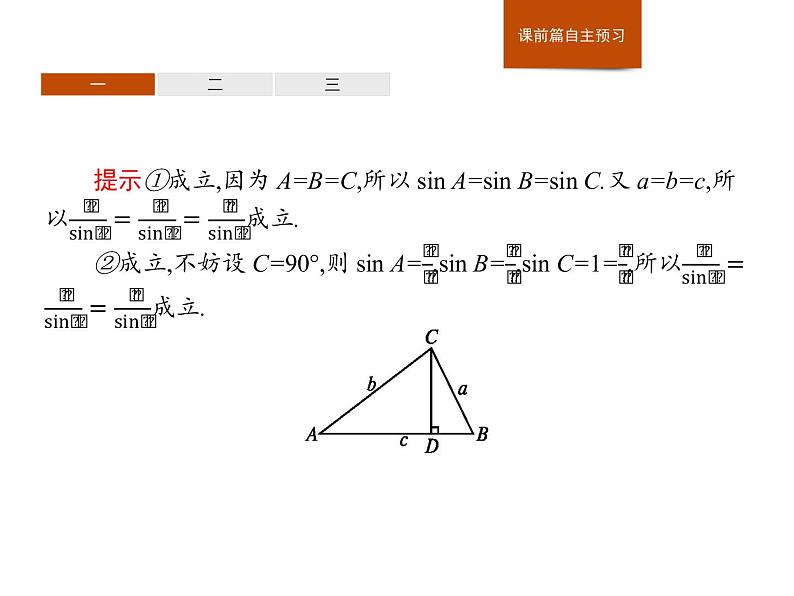
(2)在正弦定理中,三角形的各边与其所对角的正弦的比都相等,那么这个比值等于多少?与该三角形外接圆的直径有什么关系?
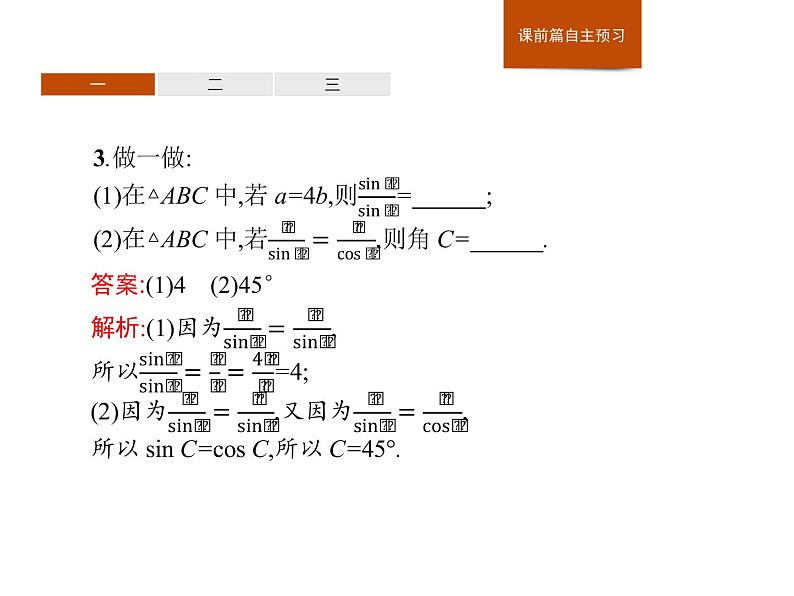
答案:(1)4　(2)45°
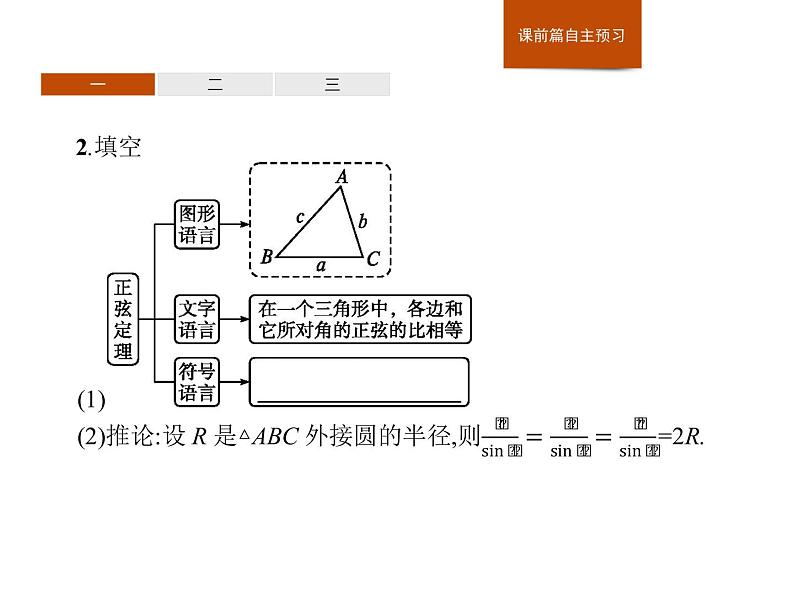
二、正弦定理的变形1.思考正弦定理揭示了三角形中边与角的数量关系,那么根据正弦定理,怎样由边转化为角?怎样由角转化为边?2.填空正弦定理的变形(R为△ABC外接圆的半径)(1)a=2Rsin A,b=2Rsin B,c=2Rsin C; (3)a∶b∶c=sin A∶sin B∶sin C. 
3.做一做(1)在△ABC中,若asin A+bsin B=csin C,则角C=　　　; (2)在△ABC中,若2asin C= c,则角A=　　　. 答案:(1)90°　(2)45°或135°
三、三角形的面积公式1.思考(1)常用的三角形面积公式是什么?(2)在三角形中如何用三角形的边和角表示某一条边上的高?提示ha=bsin C=csin B,hb=asin C=csin A,hc=bsin A=asin B.(3)能否用三角形的边和角表示三角形的面积?
3.做一做(1)在△ABC中,若AB=3,BC=4,B=120°,则△ABC的面积等于　　　　　; (2)在△ABC中,若a=2,b=8,S△ABC=4,则C=　　　　. 
已知两角和一边解三角形例1在△ABC中,已知B=30°,C=105°,b=4,解三角形.分析由三角形的内角和定理可求A的度数.根据正弦定理可求a,c.解:因为B=30°,C=105°,所以A=180°-(B+C)=180°-(30°+105°)=45°.
反思感悟 已知两角及一边解三角形的解题方法1.若所给边是已知角的对边,可先由正弦定理求另一边,再由三角形的内角和定理求出第三个角,最后由正弦定理求第三边.2.若所给边不是已知角的对边,则先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
已知两边和其中一边的对角解三角形例2在△ABC中,已知下列条件,解三角形:分析先利用正弦定理求角B,再根据三角形的内角和定理求角C,最后利用正弦定理求边c.
反思感悟 已知三角形的两边和其中一边的对角时解三角形的方法(1)首先由正弦定理求出另一边对角的正弦值.(2)当已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角唯一.(3)当已知的角为小边所对的角时,不能判断另一边所对的角为锐角,这时由正弦值可求得两个角,要分类讨论.
延伸探究 本例中,将条件改为“a=5,b=2,B=120°”,解三角形.
判断三角形的形状例3在△ABC中,若(a-ccs B)sin B=(b-ccs A)sin A,判断△ABC的形状.
反思感悟 判断三角形的形状,就是根据题目条件,分析其是不是等腰三角形、直角三角形、等边三角形、等腰直角三角形、锐角三角形、钝角三角形等.利用正弦定理判断三角形形状的方法如下:
延伸探究本例中,将条件改为“在△ABC中,若(a-acs B)·sin B=(b-ccs C)sin A”,判断△ABC的形状.解:因为(a-acs B)sin B=(b-ccs C)sin A,所以asin B-acs Bsin B=bsin A-ccs Csin A,而由正弦定理可知asin B=bsin A,所以acs Bsin B=ccs Csin A,即sin Acs Bsin B=sin Ccs Csin A,所以cs Bsin B=sin Ccs C,即sin 2B=sin 2C,所以2B=2C或2B+2C=180°,即B=C或B+C=90°,故△ABC是等腰三角形或直角三角形.
三角形面积公式的应用例4计算下列各三角形的面积.(1)在△ABC中,a=5,c=3,B=150°;(2)在△ABC中,a=8,b=8 ,A=30°;(3)在△ABC中,a=2,b=3,c=4.分析(1)可直接套用面积公式求解;(2)先利用正弦定理求出角C,再利用S= absin C计算面积;(3)先利用余弦定理求出任意一角的余弦值,再求得该角的正弦值,最后套用面积公式计算.
反思感悟 三角形面积的求解思路1.求三角形面积时,由于三角形面积公式有不同形式,因此实际使用时要结合题目的条件灵活运用,必须在两边及其夹角都已知或能求出的前提下才能使用.2.计算三角形面积时,若选择公式后有未知的边或角,应先利用正、余弦定理求出需要的边或角,再套用公式计算.
对三角形解的个数的探究已知三角形的两角和任意一边,求其他的边和角,此时有唯一解,即当三角形的两角和任意一边确定时,三角形被唯一确定.已知三角形的两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.因此“已知两边和其中一边的对角,求另一边的对角”时,需要分析三角形解的情况,下面以已知a,b和角A解三角形为例进行说明.由正弦定理、正弦函数的有界性及三角形的性质可得在△ABC中,已知a,b和角A时,解的情况如下:
发散探讨三角形解的个数也可由三角形中“大边对大角”来判定.设A为锐角,若a≥b,则A≥B,从而B为锐角,有一解.若a1,即a典例下列对三角形解的个数的判断中正确的是(　　)A.a=7,b=14,∠A=30°,有两解B.a=30,b=25,∠A=150°,有一解C.a=6,b=9,∠A=45°,有两解
2.已知△ABC中,AB=6,A=30°,B=120°,则△ABC的面积为(　　)答案:C
3.在△ABC中,若A∶B∶C=2∶3∶7,则a∶b等于 (　　)答案:C
答案:75°或15°