物理人教版 (新课标)4 法拉第电磁感应定律同步达标检测题

这是一份物理人教版 (新课标)4 法拉第电磁感应定律同步达标检测题，共9页。试卷主要包含了下列几种说法中正确的是等内容，欢迎下载使用。

基础夯实


1．(2010·南京六中期中)下列几种说法中正确的是( )


A．线圈中磁通量变化越大，线圈中产生的感应电动势一定越大


B．线圈中磁通量越大，产生的感应电动势一定越大


C．线圈放在磁场越强的位置，产生的感应电动势一定越大


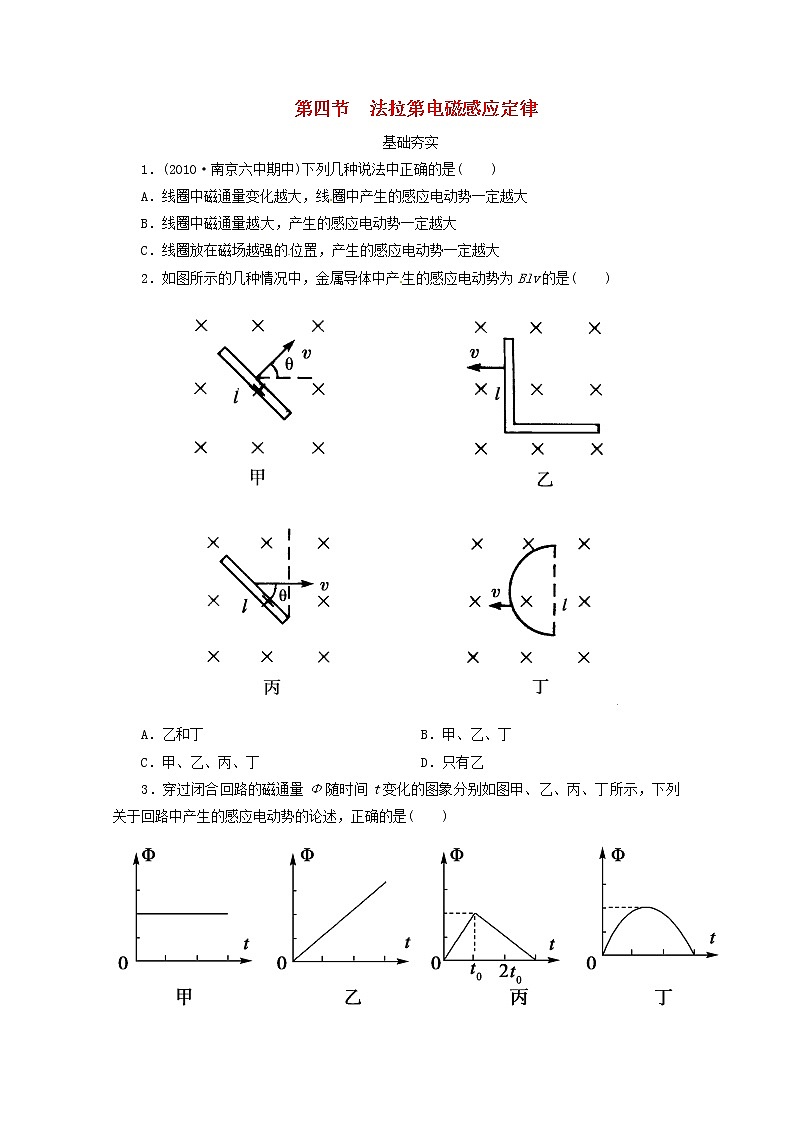
2．如图所示的几种情况中，金属导体中产生的感应电动势为Blv的是( )








A．乙和丁 B．甲、乙、丁


C．甲、乙、丙、丁 D．只有乙


3．穿过闭合回路的磁通量Φ随时间t变化的图象分别如图甲、乙、丙、丁所示，下列关于回路中产生的感应电动势的论述，正确的是( )





A．图甲中回路产生的感应电动势恒定不变


B．图乙中回路产生的感应电动势一直在变大


C．图丙中回路在0～t0时间内产生的感应电动势大于t0～2t0时间内产生的感应电动势


D．图丁回路产生的感应电动势可能恒定不变


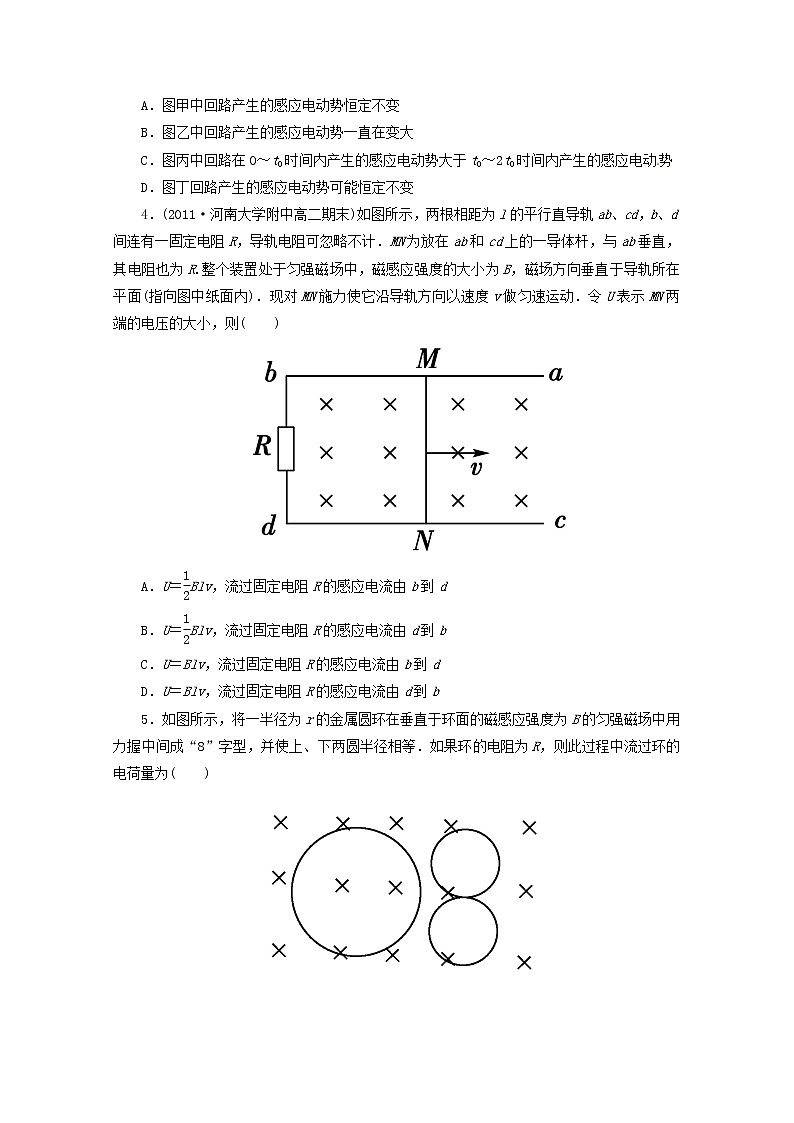
4．(2011·河南大学附中高二期末)如图所示，两根相距为l的平行直导轨ab、cd，b、d间连有一固定电阻R，导轨电阻可忽略不计．MN为放在ab和cd上的一导体杆，与ab垂直，其电阻也为R.整个装置处于匀强磁场中，磁感应强度的大小为B，磁场方向垂直于导轨所在平面(指向图中纸面内)．现对MN施力使它沿导轨方向以速度v做匀速运动．令U表示MN两端的电压的大小，则( )





A．U＝eq \f(1,2)Blv，流过固定电阻R的感应电流由b到d


B．U＝eq \f(1,2)Blv，流过固定电阻R的感应电流由d到b


C．U＝Blv，流过固定电阻R的感应电流由b到d


D．U＝Blv，流过固定电阻R的感应电流由d到b


5．如图所示，将一半径为r的金属圆环在垂直于环面的磁感应强度为B的匀强磁场中用力握中间成“8”字型，并使上、下两圆半径相等．如果环的电阻为R，则此过程中流过环的电荷量为( )





A.eq \f(πr2B,R) B.eq \f(πr2B,2R)


C．0 D.eq \f(3πr2B,4R)


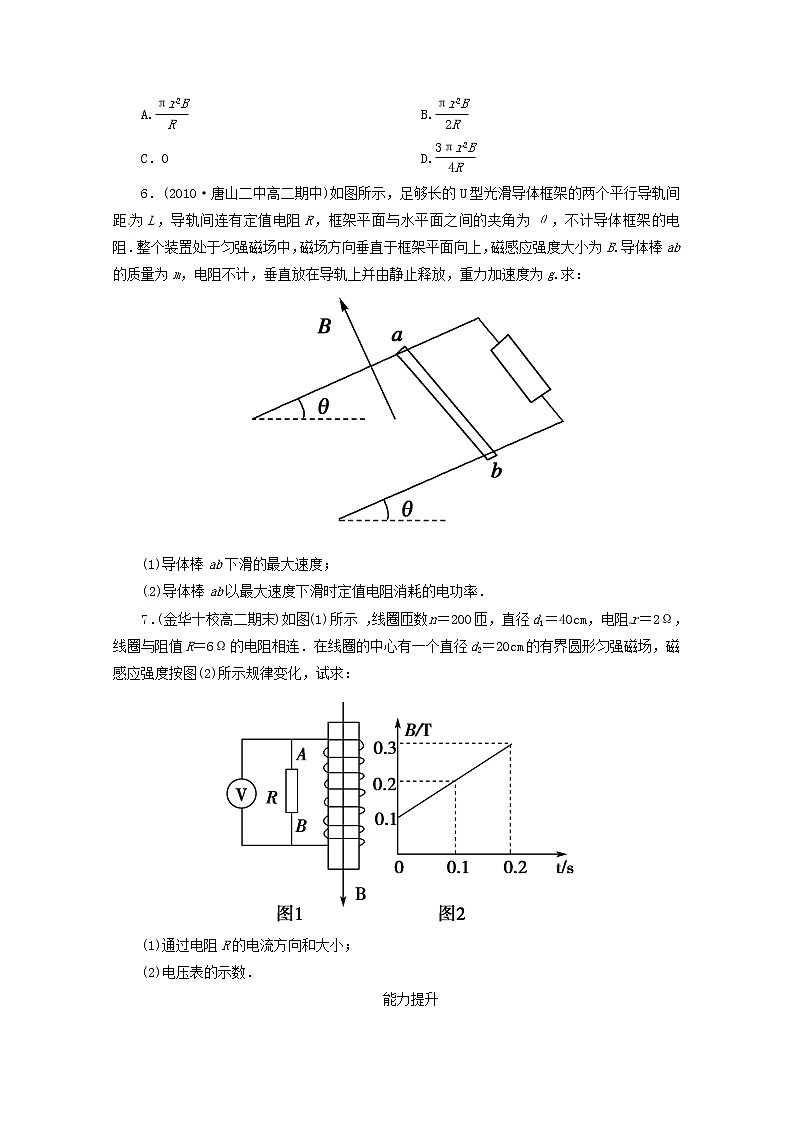
6．(2010·唐山二中高二期中)如图所示，足够长的U型光滑导体框架的两个平行导轨间距为L，导轨间连有定值电阻R，框架平面与水平面之间的夹角为θ，不计导体框架的电阻．整个装置处于匀强磁场中，磁场方向垂直于框架平面向上，磁感应强度大小为B.导体棒ab的质量为m，电阻不计，垂直放在导轨上并由静止释放，重力加速度为g.求：





(1)导体棒ab下滑的最大速度；


(2)导体棒ab以最大速度下滑时定值电阻消耗的电功率．


7．(金华十校高二期末)如图(1)所示 ，线圈匝数n＝200匝，直径d1＝40cm，电阻r＝2Ω，线圈与阻值R＝6Ω的电阻相连．在线圈的中心有一个直径d2＝20cm的有界圆形匀强磁场，磁感应强度按图(2)所示规律变化，试求：


[来源:Z。xx。k.Cm]


(1)通过电阻R的电流方向和大小；


(2)电压表的示数．


能力提升


1．(2010·潍坊市高二期中)如图所示，水平放置的平行金属导轨间距为l，左端与一电阻R相连．导轨间有竖直向下的匀强磁场，磁场的磁感应强度为B.金属杆ab垂直于两导轨放置，电阻为r，与导轨间无摩擦．现对杆ab施加向右的拉力，使杆ab向右以速度v匀速运动，则( )





A．金属杆中的电流由a到b


B．金属杆a端的电势高于b端的电势


C．拉力F＝eq \f(B2l2v,R)


D．R上消耗的功率P＝(eq \f(Blv,R＋r))2R


2．在匀强磁场中，a、b是两条平行金属导轨，而c、d为串有电流表、电压表的两金属棒，如图所示，两棒以相同的速度向右匀速运动，则以下结论正确的是( )





A．电压表有读数，电流表没有读数


B．电压表有读数，电流表也有读数


C．电压表无读数，电流表有读数


D．电压表无读数，电流表也无读数


3．(2011·天水模拟)如图甲所示．若磁感应强度B随时间t变化的关系如图乙所示，那么第3s内线圈中感应电流的大小与其各处所受安培力的方向是( )





A．大小恒定，沿顺时针方向与圆相切


B．大小恒定，沿着圆半径指向圆心


C．逐渐增加，沿着圆半径离开圆心


D．逐渐增加，沿逆时针方向与圆相切


4．粗细均匀的电阻丝围成的正方形框置于有界匀强磁场中，磁场方向垂直于线框平面，其边界与正方形线框的边平行．现使线框以同样大小的速度沿四个不同方向平移出磁场，如下图所示，则在移出过程中线框的一边ab两点间电势差绝对值最大的是( )





5．(2011·银川模拟)如图所示，半径为a的圆环电阻不计，放置在垂直于纸面向里，磁感应强度为B的匀强磁场中，环内有一导体棒，电阻为r，可以绕环匀速转动．将电阻R，开关S连接在环上和棒的O端，将电容器极板水平放置，两极板间距为d，并联在电阻R和开关S两端，如图所示．





(1)开关S断开，极板间有一带正电q、质量为m的粒子恰好静止，试判断OM的转动方向和角速度的大小．


(2)当S闭合时，该带电粒子以eq \f(1,4)g的加速度向下运动，则R是r的几倍？


6．如图所示，矩形线圈在0.01s内由原始位置Ⅰ转落至位置Ⅱ.已知ad＝5×10－2m，ab＝20×10－2m，匀强磁场的磁感应强度B＝2T，R1＝R3＝1Ω，R2＝R4＝3Ω.求：





(1)平均感应电动势；


(2)转落时，通过各电阻的平均电流．(线圈的电阻忽略不计)


D．线圈中磁通量变化越快，线圈中产生的感应电动势越大





详解答案


1答案：D


解析：感应电动势的大小与磁通量的变化率成正比，磁通量的变化率是表征磁通量变化快慢的物理量，磁通量变化越快，磁通量变化率越大，感应电动势越大，D选项对；感应电动势大小与磁通量变化的大小、磁通量的大小及线圈所在处的磁场强弱均无直接关系，ABC选项错．


2答案：B


3答案：C


解析： 根据E＝neq \f(ΔΦ,Δt)可知：图甲中E＝0，A错；图乙中E为恒量，B错；图丙中0～t0时间内的E1大于t0～2t0时间内的E2，C正确；图丁中E 为变量，D错．


4答案：A


解析：导体杆向右匀速运动产生的感应电动势为Blv，R和导体杆形成一个串联电路，由分压原理得U＝eq \f(Blv,R＋R)·R＝eq \f(1,2)Blv，由右手定则可判断出感应电流方向由N→M→b→d，所以A选项正确．


5答案：B


解析：通过环横截面的电荷量只与磁通量的变化量和环的电阻有关，与时间等其他量无关，因此，ΔΦ＝Bπr2－2×Bπeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(r,2)))2＝eq \f(1,2)Bπr2，电荷量q＝eq \f(ΔΦ,R)＝eq \f(πr2B,2R).


6答案：(1)eq \f(mgRsinθ,B2L2) (2)P＝eq \f(mgsinθ2R,B2L2)


解析：(1)mgsinθ＝BIL＝eq \f(B2L2vm,R)得vm＝eq \f(mgRsinθ,B2L2).


(2)P＝F·vm＝mgsinθ·vm＝eq \f(mgsinθ2R,B2L2).


7答案：(1)eq \f(π,4)A 方向由B流向A


(2)1.5πV


解析：(1)电流方向从B流向A


由E＝neq \f(Δφ,Δt)可得 ：E＝neq \f(πd\\al(2,2)ΔB,4Δt)


I＝eq \f(E,R＋r)＝eq \f(nπd\\al(2,2)ΔB,4ΔtR＋r)＝eq \f(π,4)A.


(2)U＝IR，解得：U＝1.5πV.





能力提升


1答案：BD


解析：由右手定则判定电流方向由b→a，a端电势高于b端，A错B对；F＝BIl＝eq \f(B2l2v,R＋r)，C错；P＝I2R＝(eq \f(Blv,R＋r))2R，D对．


2答案：D


解析：以a、b、c、d四根导线围成的回路为研究对象，在两棒匀速运动时，回路没有磁通量变化，故Ⓐ、中没有电流产生，均无读数．


3答案：B


解析：由图乙知，第3s内磁感应强度B逐渐增大，变化率恒定，根据法拉第电磁感应定律知感应电动势、感应电流的大小恒定．再由楞次定律知，线圈面积有缩小的趋势，故线圈各处所受安培力的方向沿半径指向圆心．B选项正确．


4答案：B[来源]


解析：上述四个图中，切割边所产生的电动势大小均相等(E)，回路电阻均为4r(每边电阻为r)，则电路中的电流亦相等，即I＝eq \f(E,4r)，只有B图中，ab为电源，故Uab＝I·3r＝eq \f(3,4)E.其他情况下，Uab＝I·r＝eq \f(1,4)E，故B选项正确．


5答案：(1)OM应绕O点逆时针转动 eq \f(2mgd,qBa2) (2)3


解析：(1)由于粒子带正电，故电容器上极板为负极，根据右手定则，OM应绕O点逆时针方向转动．[来源:]


粒子受力平衡，则：mg＝qeq \f(U,d)


E＝eq \f(1,2)Ba2ω


当S断开时，U＝E，


解得：ω＝eq \f(2mgd,qBa2).


(2)当S闭合时，根据牛顿第二定律：


mg－qeq \f(U′,d)＝m·eq \f(1,4)g


U′＝eq \f(E,R＋r)·R


解得：eq \f(R,r)＝3.


6答案：(1)1V (2)0.25A


解析：线圈由位置Ⅰ转落至位置Ⅱ的过程中，穿过线圈的磁通量Φ发生变化，即产生感应电动势，视这一线圈为一等效电源，线圈内部为内电路，线圈外部为外电路，然后根据闭合电路欧姆定律求解．


(1)设线圈在位置Ⅰ时，穿过它的磁通量为Φ1，线圈在位置Ⅱ时，穿过它的磁通量为Φ2，有


Φ1＝BSsin30°＝1×10－2Wb，Φ2＝2×10－2Wb，


所以ΔΦ＝Φ2－Φ1＝1×10－2Wb.


根据电磁感应定律可得E＝eq \f(ΔΦ,Δt)＝eq \f(1×10－2,0.01)V＝1V.


(2)将具有感应电动势的线圈等效为电源，其外电路的总电阻


R＝eq \f(R1＋R2,2)＝eq \f(1＋3,2)Ω＝2Ω.


根据闭合电路欧姆定律得总电流


I＝eq \f(E,R＋r)＝eq \f(1,2＋0)A＝0.5A.


通过各电阻的电流I′＝0.25A.