冀教版八年级下册第十九章 平面直角坐标系19.4 坐标与图形的变化公开课ppt课件

这是一份冀教版八年级下册第十九章 平面直角坐标系19.4 坐标与图形的变化公开课ppt课件，共15页。PPT课件主要包含了问题思考，探究1点的平移，探究2图形的平移，×2×45，解1如图所示等内容，欢迎下载使用。

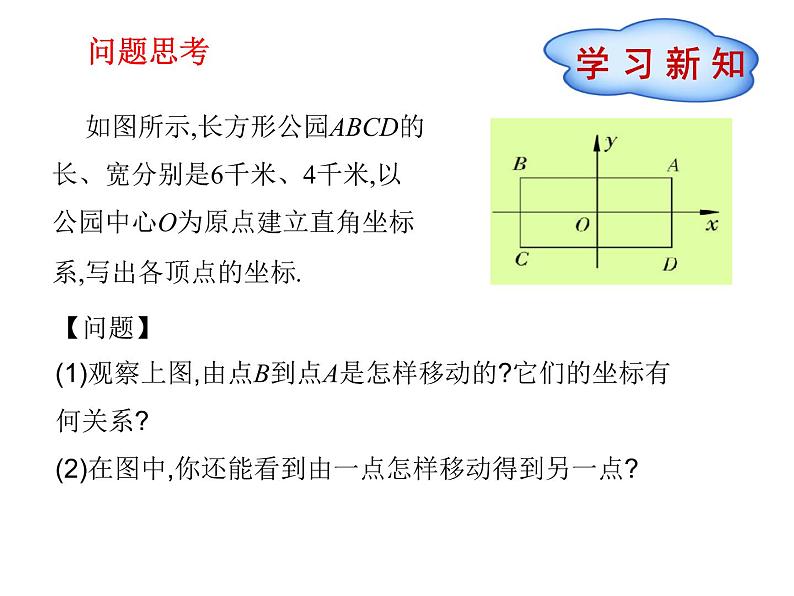
如图所示,长方形公园ABCD的长、宽分别是6千米、4千米,以公园中心O为原点建立直角坐标系,写出各顶点的坐标.
【问题】(1)观察上图,由点B到点A是怎样移动的?它们的坐标有何关系?(2)在图中,你还能看到由一点怎样移动得到另一点?
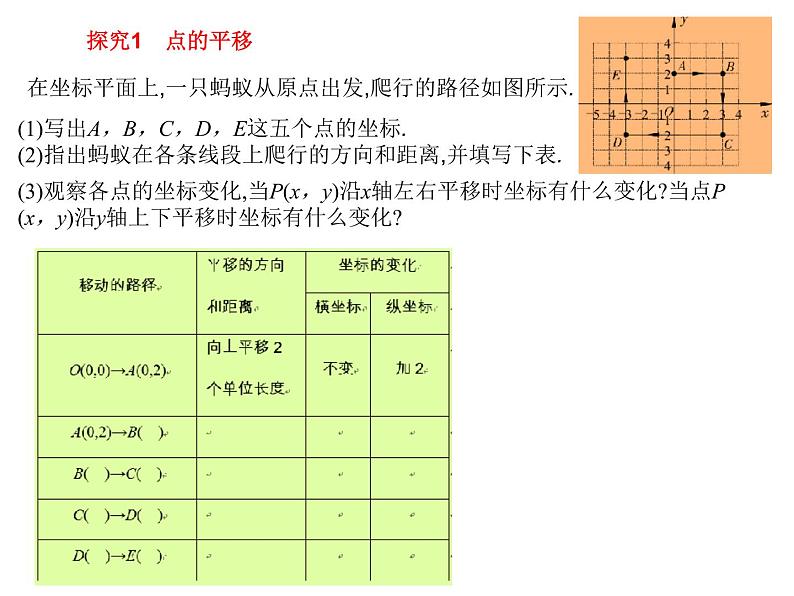
在坐标平面上,一只蚂蚁从原点出发,爬行的路径如图所示.
(1)写出A，B，C，D，E这五个点的坐标.(2)指出蚂蚁在各条线段上爬行的方向和距离,并填写下表.
(3)观察各点的坐标变化,当P(x，y)沿x轴左右平移时坐标有什么变化?当点P(x，y)沿y轴上下平移时坐标有什么变化?
【总结】　点沿x轴平移时,纵坐标不变,横坐标左减右加;点沿y轴平移时,横坐标不变,纵坐标上加下减.
如图所示,在平面直角坐标系中,长方形ABCD各顶点的坐标分别为A(-2，1),B(2，1)，C(2，3)，D(-2，3).将长方形ABCD沿x轴的方向向右平移5个单位长度,得到长方形A1B1C1D1.请写出长方形A1B1C1D1各顶点的坐标,并指出对应顶点坐标的变化规律.
解:将长方形ABCD沿x轴的方向向右平移5个单位长度,各顶点移动的方向一致,移动的距离都是5个单位长度.因此,平移后的长方形A1B1C1D1各顶点的坐标为A1(3，1)，B1(7，1)，C1(7，3)，D1(3，3).
顶点坐标的变化规律为:长方形A1B1C1D1各顶点的横坐标是将长方形ABCD各顶点的横坐标都增加5,纵坐标不变而得到的.
探究3　深化理解,总结规律
1.在例题的图中,将长方形ABCD沿y轴的方向向下平移4个单位长度,画出平移后的长方形,写出各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的.
2.若将长方形ABCD先沿x轴的方向向右平移6个单位长度,再沿y轴的方向向下平移5个单位长度,画出平移后的长方形,写出其各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的.
平移后的长方形各顶点纵坐标是由长方形ABCD各顶点的纵坐标都减少4,横坐标不变得到的.
平移后的长方形各顶点横坐标是由长方形ABCD各顶点横坐标增加6,纵坐标是由其纵坐标减少5得到的.
【思考】　在平面直角坐标系中,对于坐标平面上任意一点P(x，y)，将它沿坐标轴方向平移,点的横纵坐标有什么变化.
总结:在直角坐标系中,对于坐标平面上任意一点P(x,y).将它沿x轴的方向向右(或向左)平移k个单位长度,相当于这个点的横坐标增加(或减少)k,纵坐标不变,即点P(x,y)平移到点P'(x+k,y)(或P'(x-k,y));将它沿y轴方向向上(或向下)平移k个单位长度,相当于这个点的横坐标不变,纵坐标增加(或减少)k,即点P(x,y)平移到点P″(x,y+k)(或P″(x,y-k)).
[知识拓展]　直角坐标系中,沿横轴平移,图形上每一点的纵坐标不变,而横坐标增减,简记“左减右加”;沿纵轴平移,横坐标不变,纵坐标增减,简记“上加下减”.“左减右加,上加下减”也可这样理解:沿x轴(y轴)正方向平移,则横(纵)坐标加上平移的单位数量,沿x轴(y轴)负方向平移,则横(纵)坐标减去平移的单位数量即可.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数k,得到的新图形就是把原图形向右(或向左)平移k个单位长度;如果把一个图形各个点的纵坐标都加(或减去)一个正数k,得到的新图形就是把原图形向上(或向下)平移k个单位长度.
解析:将点M(2,1)向下平移2个单位长度后,横坐标不变,纵坐标减去2即可得到平移后点N的坐标,则点N的坐标为(2,1-2),即(2,-1).故选A.
1.如图所示,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为(　　)A.(2,-1) B.(2,3)C.(0,1) D.(4,1)
解析:由图可知点A的坐标为(0,1),平移到点C(4,2),∴平移的规律为横坐标加4,纵坐标加1,∵点B的坐标为(3,3),∴点D的坐标是(7,4).故选C.
2.如图所示,把线段AB平移,使得点A到达点C(4,2),点B到达点D,那么点D的坐标是(　　)A.(7，3) B.(6，4)C.(7，4) D.(8，4)
3.将点M(-1,-5)向右平移3个单位长度得到点N,则点N所在的象限是(　　)A.第一象限B.第二象限C.第三象限D.第四象限
解析:点M(-1,-5)向右平移3个单位长度,得到点N的坐标为(2,-5),故点N在第四象限.故选D.
4.(2016·菏泽中考)如图所示,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为(　　)A.2　　　B.3C.4　　　D.5
解析:由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别为2,3,可得A点向右平移了1个单位,由此得线段AB的平移规律是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选A.
解析:将三角形上各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相比向左平移了3个单位.故选B.
5.在平面直角坐标系中,将三角形各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相比(　　)A.向右平移了3个单位B.向左平移了3个单位C.向上平移了3个单位D.向下平移了3个单位
6.如图所示,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A,B的坐标;(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',求△A'B'C'的三个顶点的坐标;(3)求△ABC的面积.
解析:(1)点A在第四象限,横坐标为正,纵坐标为负,点B的第一象限,横纵坐标均为正;(2)让三个点的横坐标减2,纵坐标加1即为平移后的坐标;(3)△ABC的面积等于长为3,宽为4的长方形的面积减去2个直角边长为1,3和一个直角边长为2,4的直角三角形的面积,把相关数值代入即可求解.
解:(1)点A,B的坐标分别为A(2,-1),B(4,3).(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则△A'B'C'的三个顶点的坐标分别是A'(0,0),B'(2,4),C'(-1,3).(3)△ABC的面积= 3×4-2× ×1×3- ×4=5.
7.如图所示,已知单位长度为1的方格中有个△ABC. (1)请画出△ABC向上平移3格再向右平移2格所得的△A'B'C';(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B、点B'的坐标.
解析:(1)把3个顶点向上平移3格再向右平移2格,顺次连接各顶点即可;(2)以点A为坐标原点,建立平面直角坐标系,找到所求的点,并写出它们的坐标即可.
解:(1)如图可得△A'B'C'.(2)如图所示,以点A为坐标原点建立平面直角坐标系,则B(1，2)，B‘(3，5).
8.将△ABC向右平移4个单位长度,再向下平移5个单位长度.(1)作出平移后的△A‘B’C‘；(2)求出△A'B'C'的面积.
解析:(1)根据题意,直接作出平移后的△A'B'C'.(2)用长为8,宽为7的长方形的面积减去三个小直角三角形的面积,即可求得△A'B'C'的面积.
(2)△A'B'C'的面积=7×8- ×3×7- ×5×2 - ×8×5=20.5.