冀教版八年级下册22.2 平行四边形的判断优质课件ppt

这是一份冀教版八年级下册22.2 平行四边形的判断优质课件pptPPT课件主要包含了平行四边形判定定理1，平行四边形判定定理2，练一练，平行四边形判定定理3等内容，欢迎下载使用。
平行四边形的性质平行四边形的对角相等。平行四边形的对边平行且相等。平行四边形的两条对角线互相平分。平行四边形是中心对称图形，对称中心是两条对角线的交点。
根据定义，我们可以知道“两组对边分别平行的四边形是平行四边形”，那么是否还有其他什么条件也可以判定一个四边形是平行四边形？
猜想：两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形。一组对边平行另一组对边相等的四边形是平行四边形。两组对角相等的四边形是平行四边形。对角线互相平分的四边形是平行四边形。
以上，哪个是假命题，并请举出反例。
→假命题 等腰梯形
两组对边分别相等的四边形是平行四边形。 一组对边平行且相等的四边形是平行四边形。 对角线互相平分的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形。
请逐一论证以下命题的正确性。
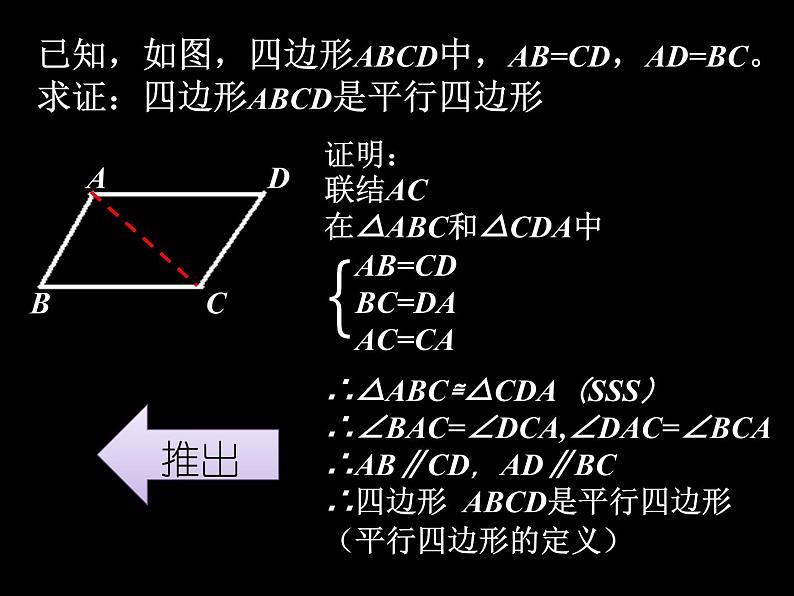
已知，如图，四边形ABCD中，AB=CD，AD=BC。 求证：四边形ABCD是平行四边形
证明：联结AC在△ABC和△CDA中
∴△ABC≌△CDA（SSS）∴∠BAC=∠DCA,∠DAC=∠BCA∴AB∥CD，AD∥BC∴四边形 ABCD是平行四边形（平行四边形的定义）
如果一个四边形的两组对边分别相等，那么这个四边形是平行四边形。简述为：两组对边分别相等的四边形是平行四边形。
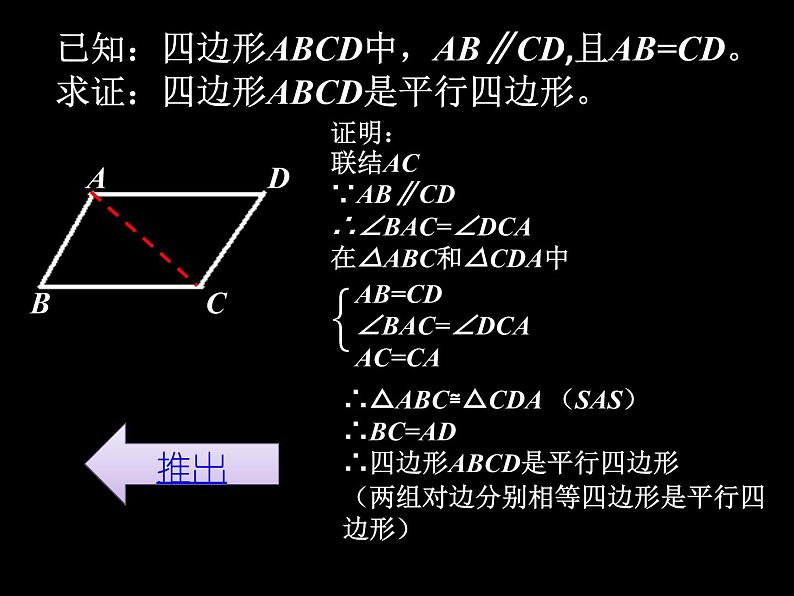
已知：四边形ABCD中，AB∥CD,且AB=CD。求证：四边形ABCD是平行四边形。
证明：联结AC∵AB∥CD∴∠BAC=∠DCA在△ABC和△CDA中
∴△ABC≌△CDA （SAS）∴BC=AD∴四边形ABCD是平行四边形（两组对边分别相等四边形是平行四边形）
如果一个四边形的一组对边平行且相等，那么这个四边形是平行四边形。简述为：一组对边平行且相等的四边形是平行四边形。
已知：如图，□ABCD中，点E、F分别在边AB和CD上，AE=CF。求证：四边形DEBF是平行四边形。
已知：如图，□ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点。 求证：四边形EFGH是平行四边形。
已知，如图，四边形ABCD的对角线AC和BD相交于点O，AO=OC，BO=OD. 求证：四边形ABCD是平行四边形。
证明：在△AOB和△COD中
∴△AOB≌△COD∴AB=CD同理可得：BC=AD∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形。
如果一个四边形的两条对角线互相平分，那么这个四边形是平行四边形。简述为：对角线互相平分的四边形是平行四边形。
已知，如图，四边形ABCD中，∠A=∠C,∠B=∠D. 求证：四边形ABCD是平行四边形
证明：在四边形ABCD中∠A+∠B+∠C+∠D=360°（多边形内角和公式）又∵∠A=∠C,∠B=∠D∴∠A+∠B=∠C+∠D=180° ∠A+∠D=∠B+∠C=180°∴AD∥BC,AB∥CD∴四边形ABCD是平行四边形（平行四边形的定义）
平行四边形的判定定理4
如果一个四边形的两组对角分别相等，那么这个四边形是平行四边形。简述为：两组对角分别相等的四边形是平行四边形。
已知，如图，□ABCD中，E、F是对角线AC上两点，且AE=CF。求证：四边形BFDE是平行四边形。