函数的初步应用PPT课件免费下载

冀教版初中数学八年级下册课文《函数的初步应用》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

一、【课程的主要内容】

0 10 20 30 40 50 t/天
12001000800600400200
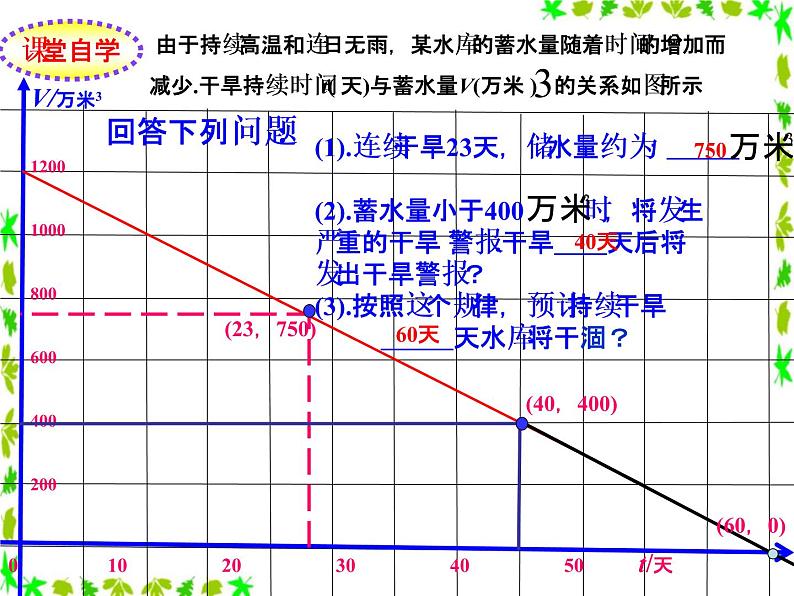
由于持续高温和连日无雨，某水库的蓄水量随着时间的增加 而减少.干旱持续时间 t( 天)与蓄水量V(万米 ) 的关系如图所示，
(1).干旱持续10天，蓄水量为多少？ 连续干旱23天呢？
分析：干旱10天求蓄水量就是已知自变量t=10时求对应的因变量的值------------数
体现在图象上就是找一个点，使点的横坐标是10，对应在图象上找到此点纵坐标的值（10，V）--------形
0 10 20 30 40 50 t/天
由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少.干旱持续时间 t( 天)与蓄水量V(万米 ) 的关系如图所示
(1).连续干旱23天，储水量约为： (2).蓄水量小于400 时，将发生严重的干旱 警报.干旱 天后将发出干旱警报？(3).按照这个规律，预计持续干旱 天水库将干涸？
0 100 200 300 400 500 x/千米
例1 某种摩托车的油箱最多可储油10升，加满油后，油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示：
根据图象回答下列问题：
(1).一箱汽油可供摩托车行驶多少千米？ (2). 摩托车每行驶100千米消耗多少升？ (3). 油箱中的剩余油量小于1升时将自 动报警.行驶多少千米后，摩托车 将自动报警？
解:观察图象:得(1)当 y=0时， x=500，因此一箱汽油可供摩托车行驶500千米.(2).x从100增加到200时， y从8减少到6，减少了2，因此摩托车每行驶100千米消耗2升汽油.(3).当y=1时，x=450，因此行驶了450千米后，摩托车将自动报警.
如何解答实际情景函数图象的信息？

二、【思考与探究】

1：理解横纵坐标分别表示的的实际意义
3：利用数形结合的思想： 将“数”转化为“形” 由“形”定“数”
2：分析已知（看已知的是自变量还是因变量），通过做x轴或y轴的垂线，在图象上找到对应的点，由点的横坐标或者纵坐标的值读出要求的值
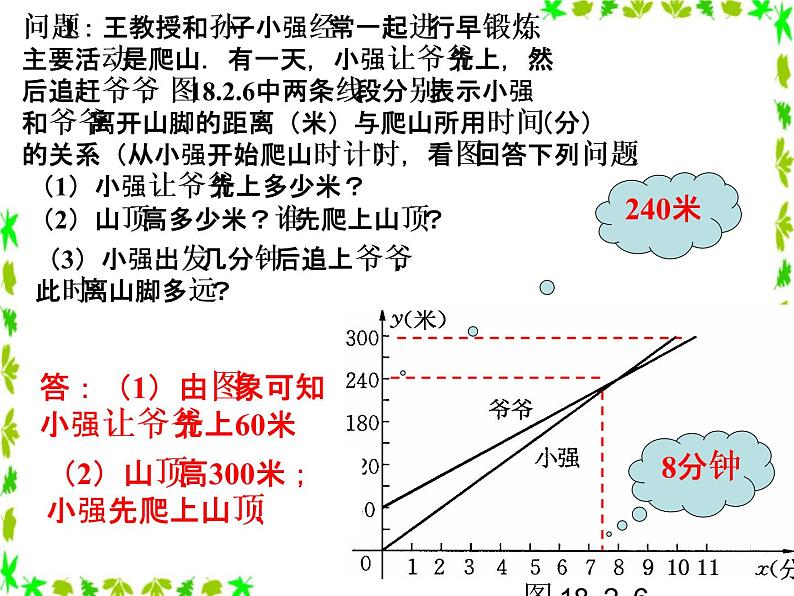
问题1：王教授和孙子小强经常一起进行早锻炼，主要活动是爬山．有一天，小强让爷爷先上，然后追赶爷爷．图18.2.6中两条线段分别表示小强和爷爷离开山脚的距离（米）与爬山所用时间（分）的关系（从小强开始爬山时计时），看图回答下列问题：
（1）小强让爷爷先上多少米？
（2）山顶高多少米？谁先爬上山顶？
答：（1）由图象可知小强让爷爷先上60米
（2）山顶高300米；小强先爬上山顶.
（3）小强出发几分钟后追上爷爷，此时离山脚多远？
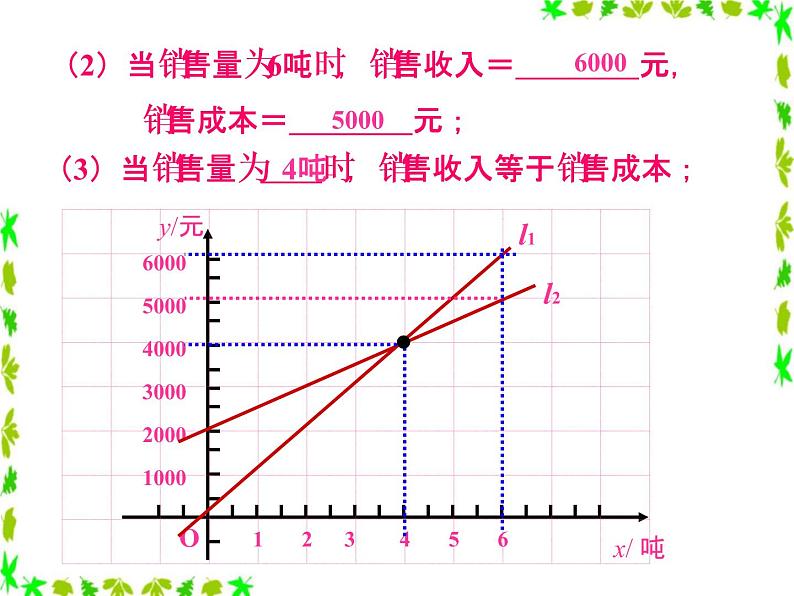
例 如图，l1反映了某公司产品的销售收入与销售量的关系，
（1）当销售量为2吨时，销售收入＝ 元， 销售成本＝ 元；
l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：
（2）当销售量为6吨时，销售收入＝ 元， 销售成本＝ 元；
（3）当销售量为 时，销售收入等于销售成本；
（4）当销售量 时，该公司赢利（收入大于成本）； 当销售量 时，该公司亏损（收入小于成本）；

三、【课堂练习】

1、某植物t天后的高度为ycm，图中的l 反映了y与t之间的关系，根据图象回答下列问题：
(1)植物刚栽的时候多高？
2）3天后该植物多高？
3）几天后该植物高度可达21cm
(1)旅客最多可免费携带多少千克行李？
⑵超过30千克后，每千克需付多少元？
3、甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示（1）这时一次 米赛跑；（2）甲、乙两人中先到达终点的是 ；（3）甲在这次赛跑中的速度为 米/秒
4、小明的爷爷吃过晚饭后，出门散步，在报亭看了一会报纸才回家，小明绘制了爷爷离家的路程s（米）与外出的时间t（分）之间的关系图（1）报亭离爷爷家 米；（2）爷爷在报亭看了 分钟报纸；（3）爷爷走去报亭的平均速度是 米/分。
4、一根蜡烛厂20cm，点燃后每小时燃烧5cm，燃烧时剩下的高度h（cm）与燃烧时间t（h）的函数关系用图象（如图）表示为（ ）
已知摄氏温度和华氏温度值有下表所示的对应关系：
（1）当摄氏温度为30℃时，华氏温度为多少度？（2）当摄氏温度为36℃时，由数值表能直接求出华氏温度吗？试写出这两种温度计量之间的函数表达式，并求摄氏温度为36℃时的华氏温度。（3）当华氏温度为140℉时，摄氏温度为多少度？
不能。若设摄氏温度为S ℃，华氏温度为H ℉，则H=1.8S+32. 96.8 ℉
某市出租车的收费标准：不超过3km计费为7元，3km后按2.4元/km计费.
(1)写出车费y(元)与路程x(km)之间的函数关系式；
(2)小亮乘出租车出行，付费12.3元，你能算出小 亮乘车的路程吗？（精确到0.1km）
(1)当0当x>3km时， y=7+2.4(x-3)
∴12.3=7+2.4(x-3)
2004年中央新闻报道，为鼓励居民节约用水，北京市将出台新的用水收费标准：①若每月每户用水不超过4m3，则按每立方米2元计算;②若每月每户用水超过4m3，则超过的部分按每立方米4.5元计算.
(1)调整水价后某户居民每月用水xm3，水费y 元， 写出y与x之间的函数关系式;
(2)甲、乙两户居民所交水费分别为7元和26 元，这两户居民该月分别用了多少m3水？
(1)当0≤x≤4m3时， y=2x(元)
当x>4m3时， y=8+4.5(x-4) (元)