鲁教版 (五四制)八年级下册6 一元二次方程的应用多媒体教学ppt课件

这是一份鲁教版 (五四制)八年级下册6 一元二次方程的应用多媒体教学ppt课件，共14页。PPT课件主要包含了例题赏析，为等腰直角三角形，整理得，不合题意舍去，解题后归纳，随堂练习，x-10，解这个方程得，小结拓展等内容，欢迎下载使用。

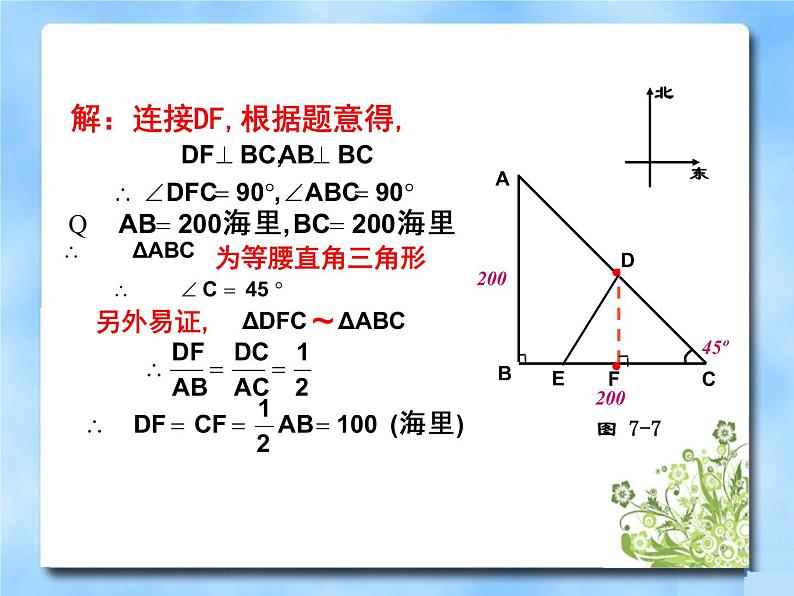
如图7-7,某海军基地位于点A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D和小岛F相距多少海里?
解：连接DF,根据题意得,
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行多少海里?(结果精确到0.1海里,其中
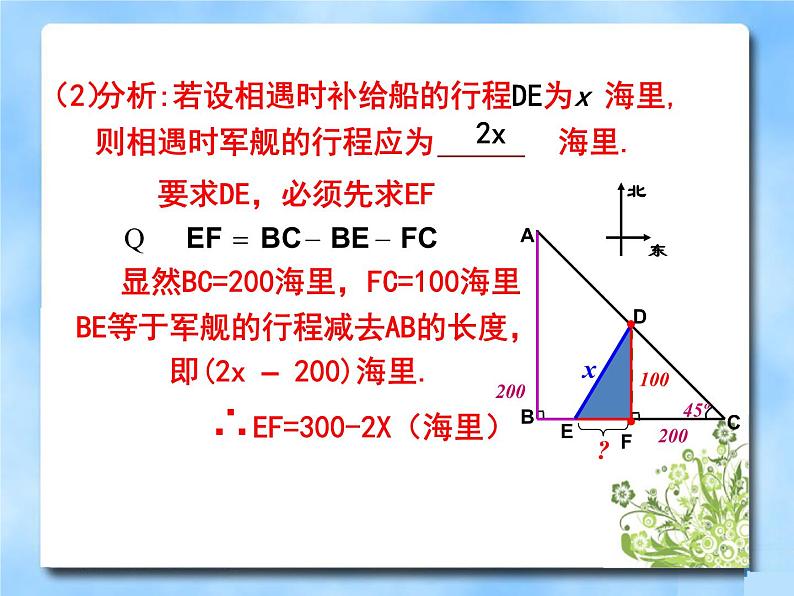
分析:若设相遇时补给船的行程DE为x 海里,则相遇时军舰的行程应为 海里.
要求DE，必须先求EF
显然BC=200海里，FC=100海里
BE等于军舰的行程减去AB的长度， 即(2x – 200)海里.
∴EF=300-2X（海里）
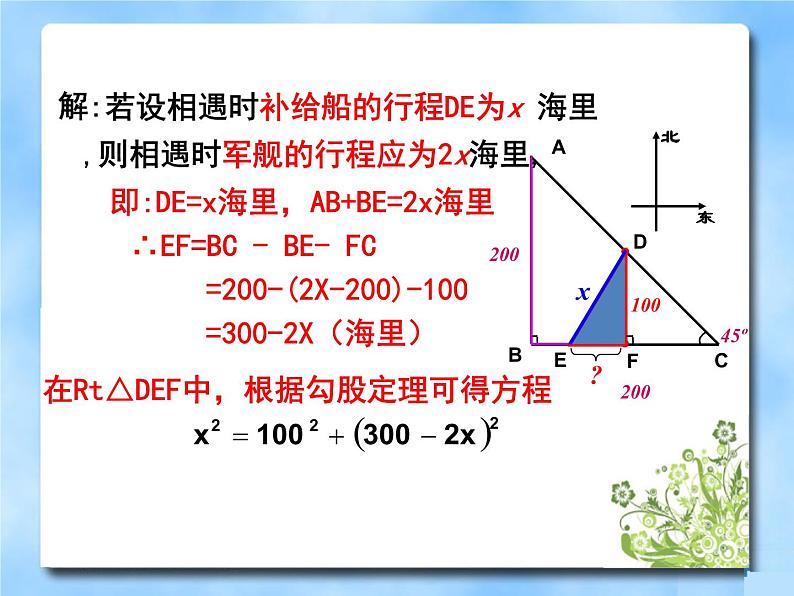
若设相遇时补给船的行程DE为x 海里,则相遇时军舰的行程应为2x海里,
即:DE=x海里，AB+BE=2x海里
∴EF=BC - BE- FC
=200-(2X-200)-100
=300-2X（海里）
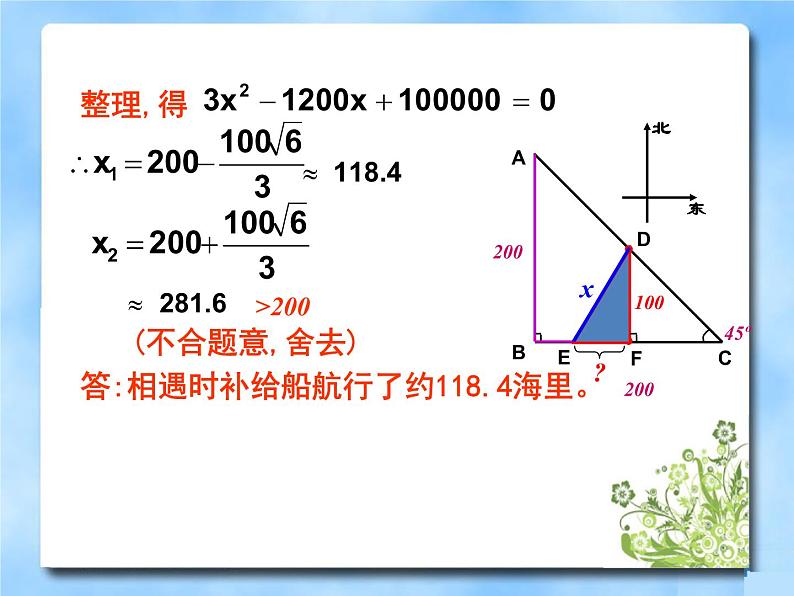
在Rt△DEF中，根据勾股定理可得方程
答:相遇时补给船航行了约118.4海里。
列方程解几何问题首先应根据题意正确地 画出图形，结合图形及其性质列出方程求解，同时切记要检验解的合理性。
1.有这样一道阿拉伯古算题:有两笔钱,一多一少,其和等于20,积等于96,多的一笔被许诺赏给赛义德,那么赛义德得到多少钱?
解:设赛以德得到的钱数为x,则少的一笔钱数为20-x,根据题意得
解: 设赛以德得到的钱数为x,则少的一笔钱数为20-x,根据题意得
原方程可变形为
答:赛义德得到的多的一笔钱数为12.
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远?”
2.《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何?”
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x-10)2=(3x)2 +102.
x1=3.5, x2=0(不合题意,舍去).
答:甲走了24.5步,乙走了10.5步.
整理得:2x2-7x=0.
∴3x=10.5, 7x=24.5.
（1）审题；（2）寻求等量关系；（3）设未知数，并根据等量关系列方程；（4）解方程并检验解的合理性；（5）作答。
利用一元二次方程解实际问题的一般步骤是：