





还剩18页未读,
继续阅读
初中数学苏科版八年级下册11.1 反比例函数图文课件ppt
展开
这是一份初中数学苏科版八年级下册11.1 反比例函数图文课件ppt,共26页。PPT课件主要包含了想一想,ykx-1,xyk,反比例函数,y3x-1,y2x2,y3x,我能行,y3y1y2,思考题等内容,欢迎下载使用。
对于一次函数 、反比例函数我们是如何学习的?
①先研究一次函数的定义 ②接着研究一次函数图象的画法 ③再研究一次函数的性质 ④最后研究一次函数的应用
①先研究反比例函数的定义②接着研究反比例函数图象的画法③再研究反比例函数的性质④最后研究反比例函数的应用
等价形式:(k ≠0)
2.你能回顾总结一下反比例函数的图象性质特征吗? 与同伴进行交流.
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内 当k<0时, 双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小 当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与 坐标轴相交
双曲线是中心对称图形.又是轴对称图形,y=x与y=-x是它的两条对称轴,原点是它的对称中心。
形状位置增减性变化趋势对称性
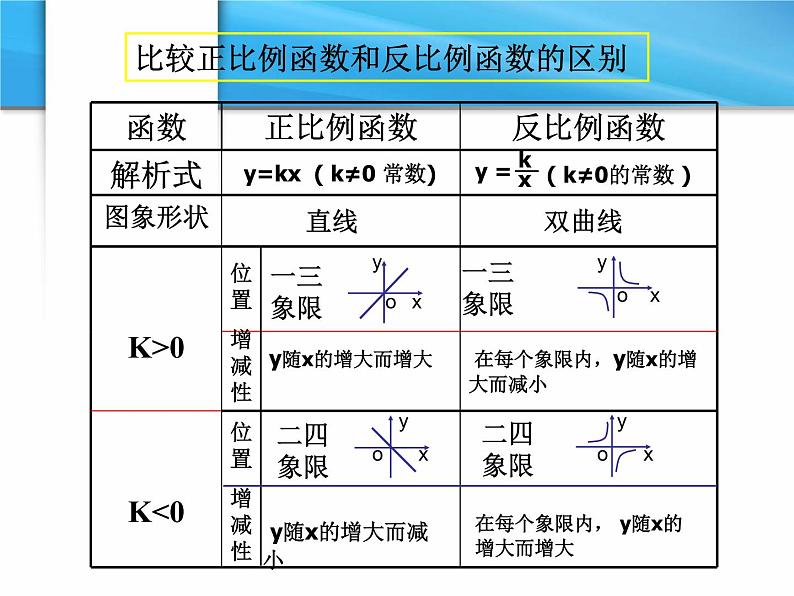
y=kx ( k≠0 常数)
双曲线
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
在每个象限内,y随x的增大而减小
下列函数中哪些是正比例函数?哪些是反比例函数? ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
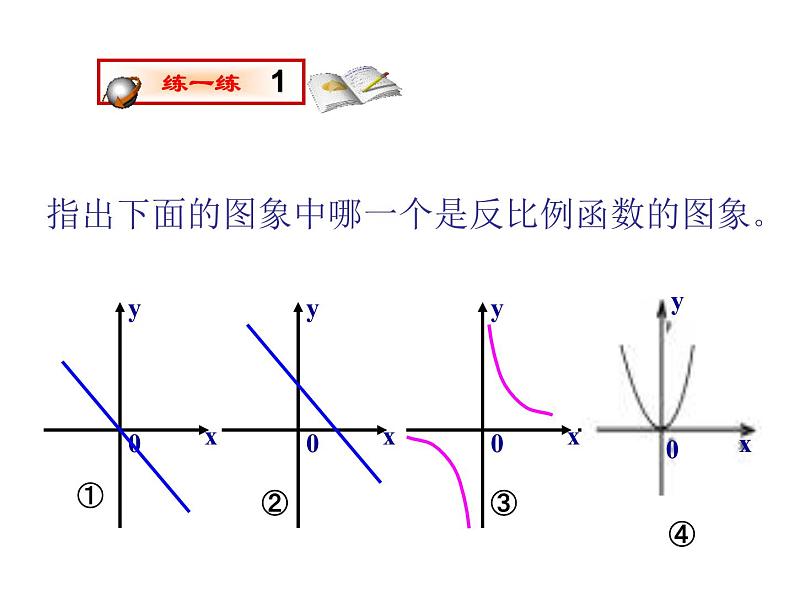
指出下面的图象中哪一个是反比例函数的图象。
函数 的图象在第________象限, 在每一象限内,y 随x 的增大而_________. 函数 的图象在第________象限, 在每一象限内,y 随x 的增大而_________.函数 ,当x>0时,图象在第____象限, y随x 的增大而_________.
已知反比例函数的图象经过点A(4,5) ,则函数的解析式为 ________; 这个函数的图象分别在第________象限,在每一象限内,y 随x 的增大而_________.判断 点B (3,-10),是否在函数 的图象上.__判断 点C (2,-5),是否在函数 的图象上.__
4.1000米长跑比赛中,速度h关于时间t的函数的图象大致是( ) .
如图,满足函数y=k(x-2)和函数y= (k≠0)的图像大致是( )A ①或③ B ②或③ C ②或④ D ①或④
你同意他的观点吗?试说明理由
1、已知反比例函数y= 的图象在第一、 三象限, 则一次函数y= -kx+4经过第 象限
练习、如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1 B、x>2C、-1<x<0或x>2 D、x<-1或0<x<2
观察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
6、如图,点P是x轴正半轴上一个动点,过点P作x轴的垂线PQ交双曲线y=
于点Q,连结OQ,点P沿x轴正方向运动时,Rt△QOP的面积( ).A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定
与反比例函数有关的面积
已知反比例函数y= ,P 为函数图象上的一点,过P做x、y轴的垂线段。
1、这样围成的矩形OAPB的面积为多少?
2、矩形面积跟什么有关?你发现其中的规律了吗?
24、(10分)如图,已知反比例函数y=- 与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;(2)△AOB的面积.
如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.求一次函数和反比例函数的解析式.
解:由已知OD=2OB=4OA=4,得A(0,-1),B(-2,0),D(-4,0). 设一次函数解析式为y=kx+b.
则一次函数解析式是
点C在一次函数图象上,当时,,即 C(-4,1).
反比例函数与一次函数的综合运用
请大家围绕以下几个问题小结本课内容:
1、反比例函数的图象是什么样子的? 它与正比例函数的图象有什么不同?
2、反比例函数的性质是什么? 它与正比例函数有什么共同点和不同点?
3、在本节课练习中你运用了哪些数学思想和方法?
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
在平面直角坐标系内,从反比例函数y=k/x(k>0))的图象上的一点分别作坐标轴的垂线段,与坐标轴围成的矩形的面积是12,请你求出该函数的解析式。
一个反比例函数的图象在第二象限,如图,点A是图象上任意一点,AM⊥x轴于点M,O是原点,如果△AOM的面积为3,求这个反比例函数的解析式。
对于一次函数 、反比例函数我们是如何学习的?
①先研究一次函数的定义 ②接着研究一次函数图象的画法 ③再研究一次函数的性质 ④最后研究一次函数的应用
①先研究反比例函数的定义②接着研究反比例函数图象的画法③再研究反比例函数的性质④最后研究反比例函数的应用
等价形式:(k ≠0)
2.你能回顾总结一下反比例函数的图象性质特征吗? 与同伴进行交流.
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内 当k<0时, 双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小 当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与 坐标轴相交
双曲线是中心对称图形.又是轴对称图形,y=x与y=-x是它的两条对称轴,原点是它的对称中心。
形状位置增减性变化趋势对称性
y=kx ( k≠0 常数)
双曲线
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
在每个象限内,y随x的增大而减小
下列函数中哪些是正比例函数?哪些是反比例函数? ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
指出下面的图象中哪一个是反比例函数的图象。
函数 的图象在第________象限, 在每一象限内,y 随x 的增大而_________. 函数 的图象在第________象限, 在每一象限内,y 随x 的增大而_________.函数 ,当x>0时,图象在第____象限, y随x 的增大而_________.
已知反比例函数的图象经过点A(4,5) ,则函数的解析式为 ________; 这个函数的图象分别在第________象限,在每一象限内,y 随x 的增大而_________.判断 点B (3,-10),是否在函数 的图象上.__判断 点C (2,-5),是否在函数 的图象上.__
4.1000米长跑比赛中,速度h关于时间t的函数的图象大致是( ) .
如图,满足函数y=k(x-2)和函数y= (k≠0)的图像大致是( )A ①或③ B ②或③ C ②或④ D ①或④
你同意他的观点吗?试说明理由
1、已知反比例函数y= 的图象在第一、 三象限, 则一次函数y= -kx+4经过第 象限
练习、如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1 B、x>2C、-1<x<0或x>2 D、x<-1或0<x<2
观察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
6、如图,点P是x轴正半轴上一个动点,过点P作x轴的垂线PQ交双曲线y=
于点Q,连结OQ,点P沿x轴正方向运动时,Rt△QOP的面积( ).A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定
与反比例函数有关的面积
已知反比例函数y= ,P 为函数图象上的一点,过P做x、y轴的垂线段。
1、这样围成的矩形OAPB的面积为多少?
2、矩形面积跟什么有关?你发现其中的规律了吗?
24、(10分)如图,已知反比例函数y=- 与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;(2)△AOB的面积.
如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.求一次函数和反比例函数的解析式.
解:由已知OD=2OB=4OA=4,得A(0,-1),B(-2,0),D(-4,0). 设一次函数解析式为y=kx+b.
则一次函数解析式是
点C在一次函数图象上,当时,,即 C(-4,1).
反比例函数与一次函数的综合运用
请大家围绕以下几个问题小结本课内容:
1、反比例函数的图象是什么样子的? 它与正比例函数的图象有什么不同?
2、反比例函数的性质是什么? 它与正比例函数有什么共同点和不同点?
3、在本节课练习中你运用了哪些数学思想和方法?
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
在平面直角坐标系内,从反比例函数y=k/x(k>0))的图象上的一点分别作坐标轴的垂线段,与坐标轴围成的矩形的面积是12,请你求出该函数的解析式。
一个反比例函数的图象在第二象限,如图,点A是图象上任意一点,AM⊥x轴于点M,O是原点,如果△AOM的面积为3,求这个反比例函数的解析式。














