

人教版华师大北师大版等通用版 中考数学 专题09 函数之一次函数和反比例函数综合问题(含解析)
展开专题09 函数之一次函数和反比例函数综合问题
中考压轴题中函数之一次函数和反比例函数综合问题,选择、填空和解答三种题型都有,内容主要包括函数图象的分析,一次函数和反比例函数的交点问题,一次函数和反比例函数的综合应用三方面的内容。
一.函数图象的分析:
1. 已知,则函数和 的图象大致是【 】
A. B. C. D.
【答案】B。
【考点】一次函数和反比例函数的性质,曲线上点的坐标与方程的关系,不等式的性质,排它法的应用。
【分析】∵,∴双曲线 的图象在一、三象限。故排除C。
又∵函数的,
∴直线与轴的交点在轴下方。故排除D。
又∵,∴,即OB<OA。故排除A。
故选B。
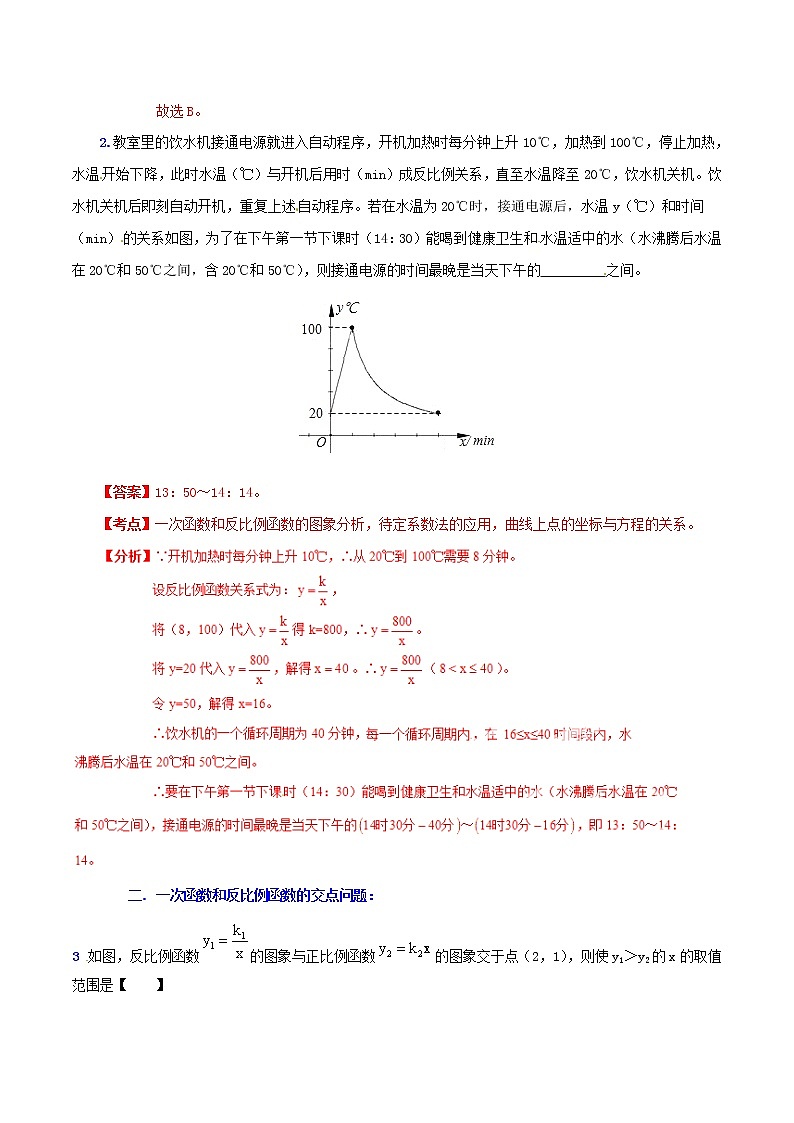
2.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至20℃,饮水机关机。饮水机关机后即刻自动开机,重复上述自动程序。若在水温为20℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在下午第一节下课时(14:30)能喝到健康卫生和水温适中的水(水沸腾后水温在20℃和50℃之间,含20℃和50℃),则接通电源的时间最晚是当天下午的 之间。
【答案】13:50~14:14。
【考点】一次函数和反比例函数的图象分析,待定系数法的应用,曲线上点的坐标与方程的关系。
二. 一次函数和反比例函数的交点问题:
3 如图,反比例函数的图象与正比例函数的图象交于点(2,1),则使y1>y2的x的取值范围是【 】
A.0<x<2 B.x>2 C.x>2或-2<x<0 D.x<-2或0<x<2
【答案】D。
4.在同一直角坐标系下,直线y=x+2与双曲线的交点的个数为【 】
A.0个 B.1个 C.2个 D.不能确定
【答案】B。
【考点】反比例函数与一次函数的交点问题,解一元二次方程。
5. 已知一次函数y1=x+m的图象与反比例函数的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
【答案】(1)y1=x+5 (2)21
【解析】
解:(1)∵当x>1时,y1>y2;当0<x<1时,y1<y2,
∴点A的横坐标为1,
代入反比例函数解析式,=y,
解得y=6,
∴点A的坐标为(1,6),
又∵点A在一次函数图象上,
∴1+m=6,
解得m=5,
∴一次函数的解析式为y1=x+5;
则点D的纵坐标为2,
∴x+5=2,
解得x=﹣3,
∴点D的坐标为(﹣3,2),
∴CD=3﹣(﹣3)=3+3=6,
点A到CD的距离为6﹣2=4,
考点:反比例函数与一次函数的交点问题.
点评:本题考查了反比例函数图象与一次函数图象的交点问题,根据已知条件先判断出点A的横坐标是解题的关键.
三. 一次函数和反比例函数的综合应用问题:
6. 如图,直线与双曲线交于E、F两点,与轴、轴分别交于A、B两点,点C,连结CA、CB、CE、CF,若,则= 。
【答案】。
【考点】直线与双曲线的综合题,曲线上点的坐标与方程的关系,等腰三角形的性质,相似三角形的性质。
【分析】在中,令,解得;令,则。
∴点A(2,0)、B(0,)。
又∵C,∴CB=。
在Rt△OAC中,由勾股定理得,CA==,∴CB=CA。
7. 如图,已知一次函数的图象交反比例函数的图象于点A、B,交轴于点C。
(1)求的取值范围;
(2)若点A的坐标是(2,4),且=,求的值和一次函数的解析式。
【答案】(1)∵反比例函数的图象在第四象限,∴,解得。
(2)∵点A(2, 4)在函数图象上,
∴,解得。
∴反比例函数解析式为。
∵一次函数的图象过点A(2, 4)、B(6,),
∴,解得。
∴一次函数的解析式是。
【考点】反比例函数图象的性质,点的坐标与方程的关系,相似三角形的判定和性质,待定系数法,解二元一次方程组。








