

还剩14页未读,
继续阅读
所属成套资源:2019高考人教版数学(理科)一轮复习全套学案
成套系列资料,整套一键下载
2019版高考数学(理)一轮精选教师用书人教通用:第8章1第1讲 空间几何体的结构特征及三视图和直观图
展开
知识点
考纲下载
空间几何体的结构及三视图和直观图
认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二测法画出它们的直观图.
会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).
空间几何体的表面积与体积
了解球、棱柱、棱锥、台的表面积和体积的计算公式.
空间点、直线、平面之间的位置关系
理解空间直线、平面位置关系的定义.
了解可以作为推理依据的公理和定理.
能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
空间中的平行关系
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理.
空间中的垂直关系
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.
空间向量及其运算
了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示.
掌握空间向量的线性运算及其坐标表示.
掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直.
立体几何中的向量方法
理解直线的方向向量与平面的法向量.
能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.
能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).
能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.
第1讲 空间几何体的结构特征及三视图和直观图
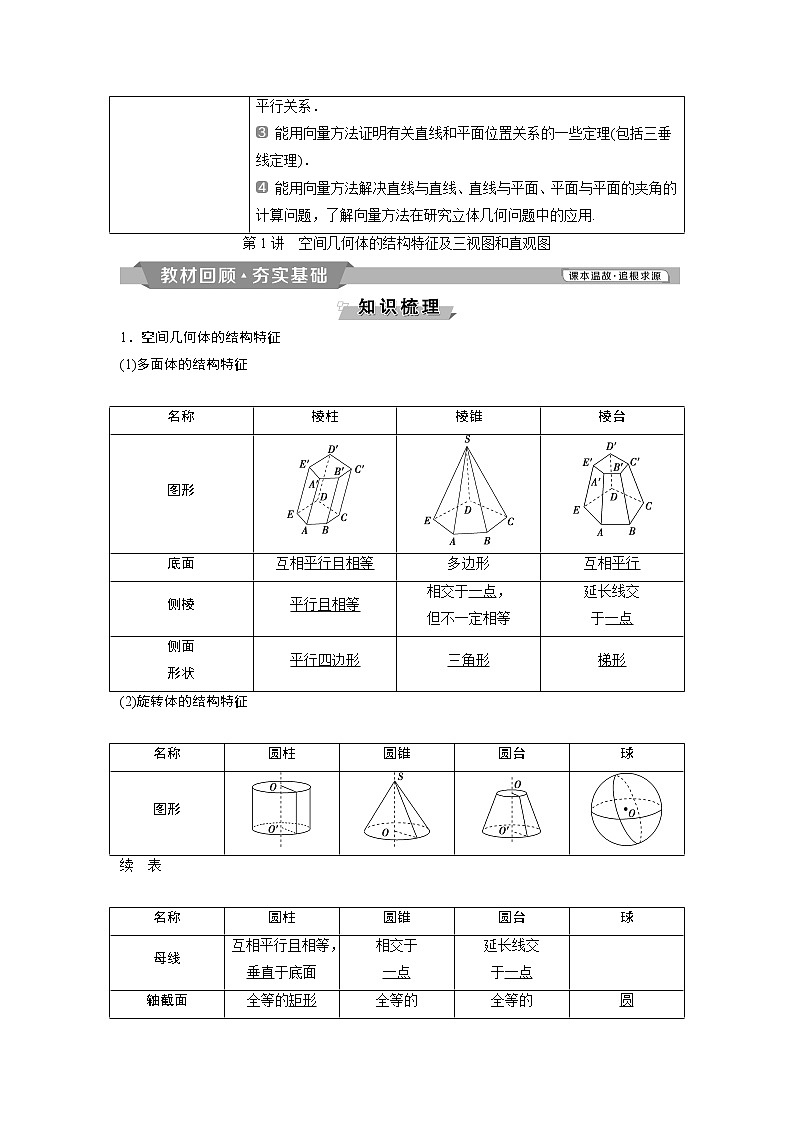
1.空间几何体的结构特征
(1)多面体的结构特征
名称
棱柱
棱锥
棱台
图形
底面
互相平行且相等
多边形
互相平行
侧棱
平行且相等
相交于一点,
但不一定相等
延长线交
于一点
侧面
形状
平行四边形
三角形
梯形
(2)旋转体的结构特征
名称
圆柱
圆锥
圆台
球
图形
续 表
名称
圆柱
圆锥
圆台
球
母线
互相平行且相等,垂直于底面
相交于
一点
延长线交
于一点
轴截面
全等的矩形
全等的
等腰三角形
全等的
等腰梯形
圆
侧面展
开图
矩形
扇形
扇环
2.直观图
(1)画法:常用斜二测画法.
(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴,y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.
3.三视图
(1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.
(2)三视图的画法
①基本要求:长对正,高平齐,宽相等.
②画法规则:正侧一样高,正俯一样长,侧俯一样宽;看到的线画实线,看不到的线画虚线.
判断正误(正确的打“√”,错误的打“×”)
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( )
(2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( )
(3)夹在两个平行的平面之间,其余的面都是梯形,这样的几何体一定是棱台.( )
(4)在正方体、球、圆锥各自的三视图中,三视图均相同.( )
(5)用两平行平面截圆柱,夹在两平行平面间的部分仍是圆柱.( )
(6)菱形的直观图仍是菱形.( )
答案:(1)× (2)× (3)× (4)× (5)× (6)×
关于空间几何体的结构特征,下列说法不正确的是( )
A.棱柱的侧棱长都相等
B.棱锥的侧棱长都相等
C.三棱台的上、下底面是相似三角形
D.有的棱台的侧棱长都相等
解析:选B.根据棱锥的结构特征知,棱锥的侧棱长不一定都相等.
若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
解析:选B.根据选项A、B、C、D中的直观图,画出其三视图,只有B项正确.
(教材习题改编)若某几何体的三视图如图所示,则该几何体为________.
答案:四棱柱与圆柱组合而成的简单组合体
在直观图(如图所示)中,四边形O′A′B′C′为菱形且边长为2 cm,则在平面直角坐标系xOy中,四边形ABCO为________,面积为________cm2.
解析:由斜二测画法的特点,知该平面图形的直观图的原图,即在平面直角坐标系xOy中,四边形ABCO是一个长为4 cm,宽为2 cm的矩形,所以四边形ABCO的面积为8 cm2.
答案:矩形 8
空间几何体的结构特征
[典例引领]
(1)下列结论正确的是( )
A.侧面都是等腰三角形的三棱锥是正三棱锥
B.六条棱长均相等的四面体是正四面体
C.有两个侧面是矩形的棱柱是直棱柱
D.用一个平面去截圆锥,底面与截面之间的部分叫圆台
(2)以下命题:
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;
③圆柱、圆锥、圆台的底面都是圆面;
④一个平面截圆锥,得到一个圆锥和一个圆台.
其中正确命题的个数为( )
A.0 B.1
C.2 D.3
【解析】 (1)底面是等边三角形,且各侧面三角形全等,这样的三棱锥才是正三棱锥,A错;斜四棱柱也有可能两个侧面是矩形,所以C错;截面平行于底面时,底面与截面之间的部分才叫圆台,D错.
(2)命题①错,因为这条边若是直角三角形的斜边,则得不到圆锥;命题②错,因为这条腰必须是垂直于两底的腰;命题③对;命题④错,必须用平行于圆锥底面的平面截圆锥才可以得到一个圆锥和一个圆台.
【答案】 (1)B (2)B
空间几何体概念辨析问题的常用方法
[通关练习]
1.给出下列命题:
①各侧面都是全等四边形的棱柱一定是正棱柱;
②对角面是全等矩形的六面体一定是长方体;
③长方体一定是正四棱柱.
其中正确的命题个数是( )
A.0 B.1
C.2 D.3
解析:选A.①直平行六面体底面是菱形,满足条件但不是正棱柱;②底面是等腰梯形的直棱柱,满足条件但不是长方体;③显然错误.
2.下列说法正确的是( )
A.以半圆的直径所在直线为旋转轴旋转形成的曲面叫做球
B.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
D.圆锥的顶点与底面圆周上任意一点的连线都是母线
解析:选D.球面和球是两个不同的概念,以半圆的直径所在直线为旋转轴旋转形成的曲面叫做球面,球面围成的几何体叫做球,A错误.对于B,如图,满足有两个面平行,其余四个面都是等腰梯形,但它不是棱台,故B错.若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.C错误.由母线的概念知,选项D正确.
空间几何体的三视图(高频考点)
空间几何体的三视图是每年高考的热点,题型为选择题或填空题,难度适中,属于中档题.高考对三视图的考查主要有以下三个命题角度:
(1)由空间几何体的直观图识别三视图;
(2)由空间几何体的三视图还原直观图;
(3)由空间几何体的部分视图画出剩余部分视图.
[典例引领]
角度一 由空间几何体的直观图识别三视图
(2018·惠州市第三次调研考试)如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )
【解析】 从几何体的左面看,对角线AD1在视线范围内,画实线,棱C1F不在视线范围内,画虚线.
【答案】 B
角度二 由空间几何体的三视图还原直观图
(2017·高考北京卷)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2
C.2 D.2
【解析】 由三视图还原为如图所示的四棱锥A-BCC1B1,
从图中易得最长的棱长为AC1===2,选B.
【答案】 B
角度三 由空间几何体的部分视图画出剩余部
分视图
(2018·广州市综合测试(一))如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为,则该几何体的俯视图可以是( )
【解析】
由题意可得该几何体可能为四棱锥,如图所示,其高为2,其底面为正方形,面积为2×2=4,因为该几何体的体积为×4×2=,满足条件,所以俯视图可以为一个直角三角形.
【答案】 D
三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的视图.先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.
(2016·高考天津卷)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( )
解析:选B.由几何体的正视图和俯视图可知该几何体为图①,故其侧(左)视图为图②.
空间几何体的直观图
[典例引领]
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6 cm,O′C′=2 cm,则原图形是( )
A.正方形 B.矩形
C.菱形 D.一般的平行四边形
【解析】
如图,在原图形OABC中,
应有OD=2O′D′=2×2=4(cm),
CD=C′D′=2 cm,
所以OC=
==6(cm),
所以OA=OC,
故四边形OABC是菱形,
因此选C.
【答案】 C
若本例中直观图为如图所示的一个边长为1 cm的正方形,则原图形的周长是多少?
解:将直观图还原为平面图形,如图.
可知还原后的图形中OB=2,AB==3,于是周长为2×3+2×1=8(cm).
斜二测画法中的“三变”与“三不变”
“三变”
“三不变”
[通关练习]
1.如图所示为一个平面图形的直观图,则它的实际形状四边形ABCD为( )
A.平行四边形 B.梯形
C.菱形 D.矩形
解析:选D.由斜二测画法可知在原四边形ABCD中DA⊥AB,并且AD∥BC,AB∥CD,故四边形ABCD为矩形.
2.在等腰梯形ABCD中,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为________.
解析:因为OE==1,
所以O′E′=,E′F′=.
所以直观图A′B′C′D′的面积为
S′=×(1+3)×=.
答案:
常见旋转体的三视图
(1)球的三视图都是半径相等的圆.
(2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形.
(3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形.
(4)水平放置的圆柱的正视图和侧视图均为全等的矩形.
根据几何体的三视图判断几何体的结构特征
(1)三视图为三个三角形,一般对应三棱锥;
(2)三视图为两个三角形,一个四边形,一般对应四棱锥;
(3)三视图为两个三角形,一个圆,一般对应圆锥;
(4)三视图为一个三角形,两个四边形,一般对应三棱柱;
(5)三视图为两个四边形,一个圆,一般对应圆柱.
明确三视图与几何体的数量关系
正(主)视图、侧(左)视图的高就是空间几何体的高;正(主)视图、俯视图的长就是空间几何体的最大长度;侧(左)视图、俯视图中的宽就是几何体的最大宽度.
易错防范
(1)台体可以看成是由锥体截得的,易忽视截面与底面平行且侧棱延长后必交于一点.
(2)空间几何体不同放置时其三视图不一定相同.
(3)对于简单组合体,若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,易忽视实虚线的画法.
1.下列说法正确的有( )
①两个面平行且相似,其余各面都是梯形的多面体是棱台;
②经过球面上不同的两点只能作一个大圆;
③各侧面都是正方形的四棱柱一定是正方体;
④圆锥的轴截面是等腰三角形.
A.1个 B.2个
C.3个 D.4个
解析:选A.①中若两个底面平行且相似,其余各面都是梯形,并不能保证侧棱会交于一点,所以①不正确;②中若球面上不同的两点恰为球的某条直径的两个端点,则过此两点的大圆有无数个,所以②不正确;③中底面不一定是正方形,所以③不正确;很明显④是正确的.
2.如图所示是水平放置的三角形的直观图,点D是△ABC的BC边的中点,AB,BC分别与y′轴、x′轴平行,则在原图中三条线段AB,AD,AC中( )
A.最长的是AB,最短的是AC
B.最长的是AC,最短的是AB
C.最长的是AB,最短的是AD
D.最长的是AC,最短的是AD
解析:选B.由条件知,原平面图形中AB⊥BC,从而AB
A.①② B.②③
C.③④ D.①⑤
解析:选D.圆锥的轴截面为等腰三角形,此时①符合条件;
当截面不过旋转轴时,
圆锥的轴截面为双曲线的一支,此时⑤符合条件;
故截面图形可能是①⑤.
4.(2018·惠州市第三次调研考试)某四棱锥的三视图如图所示,则该四棱锥最长棱的棱长为( )
A.1 B.
C. D.2
解析:选C.根据三视图,可知几何体的直观图为如图所示的四棱锥VABCD,其中VB⊥底面ABCD,且底面ABCD是边长为1的正方形,VB=1.所以四棱锥中最长棱为VD.连接BD,易知BD=,在Rt△VBD中,
VD==.
5.(2017·高考全国卷Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A.10 B.12
C.14 D.16
解析:选B.由三视图可知该多面体是一个组合体,下面是一个底面是等腰直角三角形的直三棱柱,上面是一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰长为2,直三棱柱的高为2,三棱锥的高为2,易知该多面体有2个面是梯形,这些梯形的面积之和为×2=12,故选B.
6.有一个长为5 cm,宽为4 cm的矩形,则其直观图的面积为________.
解析:由于该矩形的面积S=5×4=20(cm2),所以其直观图的面积S′=S=5(cm2).
答案:5 cm2
7.如图所示的Rt△ABC绕着它的斜边AB旋转一周得到的图形是________.
解析:过Rt△ABC的顶点C作线段CD⊥AB,垂足为D,所以Rt△ABC绕着它的斜边AB旋转一周后应得到是以CD作为底面圆的半径的两个圆锥的组合体.
答案:两个圆锥的组合体
8.已知某空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有________个.
解析:由三视图知该几何体是一个四棱锥,它的一个侧面与底面垂直,且此侧面的顶点在底面上的射影为对应底边的中点,易知其有两个侧面是直角三角形.
答案:2
9.如图,在四棱锥PABCD中,底面为正方形,PC与底面ABCD垂直,图为该四棱锥的正视图和侧视图,它们是腰长为6 cm的全等的等腰直角三角形.
(1)根据所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求PA.
解:(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形,如图,其面积为36 cm2.
(2)由侧视图可求得PD===6 cm.
由正视图可知AD=6 cm,且AD⊥PD,
所以在Rt△APD中,
PA= = =6 (cm).
10.如图所示,在侧棱长为2的正三棱锥VABC中,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF,求△AEF周长的最小值.
解:如图,将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,则线段AA1的长即为所求△AEF的周长的最小值.
取AA1的中点D,
连接VD,
则VD⊥AA1,∠AVD=60°.
在Rt△VAD中,
AD=VA·sin 60°=3,
所以AA1=2AD=6,
即△AEF周长的最小值为6.
1.某几何体的正视图和侧视图如图(1),它的俯视图的直观图是矩形O1A1B1C1,如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
A.48 B.64
C.96 D.128
解析:选C.由题图(2)及斜二测画法可知原俯视图为如图所示的平行四边形OABC,设CB与y轴的交点为D,则易知CD=2,OD=2×2=4,所以CO==6=OA,所以俯视图是以6为边长的菱形,由三视图知几何体为一个直四棱柱,其高为4,所以该几何体的侧面积为4×6×4=96.故选C.
2.一个三棱锥的正视图和俯视图如图所示,则该三棱锥的侧视图可能为( )
解析:选D.由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,故选D.
3.(2018·福建泉州模拟)某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )
A.圆弧 B.抛物线的一部分
C.椭圆的一部分 D.双曲线的一部分
解析:选D.根据几何体的三视图可得,侧视图中的虚线部分是由平行于旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选D.
4.(2018·广东文雅中学、江西南昌二中联考)某四面体的三视图如图所示,在该四面体的四个面中,直角三角形的面积和是( )
A.2 B.4 C.2+ D.4+2
解析:选C.由三视图可得原几何体如图所示,由三视图知该几何体的高PO=2,底面ABC是边长为2的等腰直角三角形,平面PAC⊥平面ABC,∠ACB=90°,则BC⊥平面PAC,所以BC⊥PC,所以直角三角形有△PBC和△ACB,易求得PC==,又BC=2,所以S△PBC=×2×=,又S△ABC=×2×2=2,所以该四面体的四个面中,直角三角形的面积和为2+,故选C.
5.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.
解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.
(2)直观图如图所示.
6.如图是一个几何体的正视图和俯视图.
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积.
解:(1)正六棱锥.
(2)其侧视图如图:
其中AB=AC,AD⊥BC,
且BC的长是俯视图中的正六边形对边的距离,
即BC=a,
AD的长是正六棱锥的高,即AD=a,
所以该平面图形的面积S=·a·a=a2.
知识点
考纲下载
空间几何体的结构及三视图和直观图
认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二测法画出它们的直观图.
会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).
空间几何体的表面积与体积
了解球、棱柱、棱锥、台的表面积和体积的计算公式.
空间点、直线、平面之间的位置关系
理解空间直线、平面位置关系的定义.
了解可以作为推理依据的公理和定理.
能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
空间中的平行关系
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理.
空间中的垂直关系
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.
空间向量及其运算
了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示.
掌握空间向量的线性运算及其坐标表示.
掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直.
立体几何中的向量方法
理解直线的方向向量与平面的法向量.
能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.
能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).
能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.
第1讲 空间几何体的结构特征及三视图和直观图
1.空间几何体的结构特征
(1)多面体的结构特征
名称
棱柱
棱锥
棱台
图形
底面
互相平行且相等
多边形
互相平行
侧棱
平行且相等
相交于一点,
但不一定相等
延长线交
于一点
侧面
形状
平行四边形
三角形
梯形
(2)旋转体的结构特征
名称
圆柱
圆锥
圆台
球
图形
续 表
名称
圆柱
圆锥
圆台
球
母线
互相平行且相等,垂直于底面
相交于
一点
延长线交
于一点
轴截面
全等的矩形
全等的
等腰三角形
全等的
等腰梯形
圆
侧面展
开图
矩形
扇形
扇环
2.直观图
(1)画法:常用斜二测画法.
(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴,y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.
3.三视图
(1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.
(2)三视图的画法
①基本要求:长对正,高平齐,宽相等.
②画法规则:正侧一样高,正俯一样长,侧俯一样宽;看到的线画实线,看不到的线画虚线.
判断正误(正确的打“√”,错误的打“×”)
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( )
(2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( )
(3)夹在两个平行的平面之间,其余的面都是梯形,这样的几何体一定是棱台.( )
(4)在正方体、球、圆锥各自的三视图中,三视图均相同.( )
(5)用两平行平面截圆柱,夹在两平行平面间的部分仍是圆柱.( )
(6)菱形的直观图仍是菱形.( )
答案:(1)× (2)× (3)× (4)× (5)× (6)×
关于空间几何体的结构特征,下列说法不正确的是( )
A.棱柱的侧棱长都相等
B.棱锥的侧棱长都相等
C.三棱台的上、下底面是相似三角形
D.有的棱台的侧棱长都相等
解析:选B.根据棱锥的结构特征知,棱锥的侧棱长不一定都相等.
若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
解析:选B.根据选项A、B、C、D中的直观图,画出其三视图,只有B项正确.
(教材习题改编)若某几何体的三视图如图所示,则该几何体为________.
答案:四棱柱与圆柱组合而成的简单组合体
在直观图(如图所示)中,四边形O′A′B′C′为菱形且边长为2 cm,则在平面直角坐标系xOy中,四边形ABCO为________,面积为________cm2.
解析:由斜二测画法的特点,知该平面图形的直观图的原图,即在平面直角坐标系xOy中,四边形ABCO是一个长为4 cm,宽为2 cm的矩形,所以四边形ABCO的面积为8 cm2.
答案:矩形 8
空间几何体的结构特征
[典例引领]
(1)下列结论正确的是( )
A.侧面都是等腰三角形的三棱锥是正三棱锥
B.六条棱长均相等的四面体是正四面体
C.有两个侧面是矩形的棱柱是直棱柱
D.用一个平面去截圆锥,底面与截面之间的部分叫圆台
(2)以下命题:
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;
③圆柱、圆锥、圆台的底面都是圆面;
④一个平面截圆锥,得到一个圆锥和一个圆台.
其中正确命题的个数为( )
A.0 B.1
C.2 D.3
【解析】 (1)底面是等边三角形,且各侧面三角形全等,这样的三棱锥才是正三棱锥,A错;斜四棱柱也有可能两个侧面是矩形,所以C错;截面平行于底面时,底面与截面之间的部分才叫圆台,D错.
(2)命题①错,因为这条边若是直角三角形的斜边,则得不到圆锥;命题②错,因为这条腰必须是垂直于两底的腰;命题③对;命题④错,必须用平行于圆锥底面的平面截圆锥才可以得到一个圆锥和一个圆台.
【答案】 (1)B (2)B
空间几何体概念辨析问题的常用方法
[通关练习]
1.给出下列命题:
①各侧面都是全等四边形的棱柱一定是正棱柱;
②对角面是全等矩形的六面体一定是长方体;
③长方体一定是正四棱柱.
其中正确的命题个数是( )
A.0 B.1
C.2 D.3
解析:选A.①直平行六面体底面是菱形,满足条件但不是正棱柱;②底面是等腰梯形的直棱柱,满足条件但不是长方体;③显然错误.
2.下列说法正确的是( )
A.以半圆的直径所在直线为旋转轴旋转形成的曲面叫做球
B.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
D.圆锥的顶点与底面圆周上任意一点的连线都是母线
解析:选D.球面和球是两个不同的概念,以半圆的直径所在直线为旋转轴旋转形成的曲面叫做球面,球面围成的几何体叫做球,A错误.对于B,如图,满足有两个面平行,其余四个面都是等腰梯形,但它不是棱台,故B错.若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.C错误.由母线的概念知,选项D正确.
空间几何体的三视图(高频考点)
空间几何体的三视图是每年高考的热点,题型为选择题或填空题,难度适中,属于中档题.高考对三视图的考查主要有以下三个命题角度:
(1)由空间几何体的直观图识别三视图;
(2)由空间几何体的三视图还原直观图;
(3)由空间几何体的部分视图画出剩余部分视图.
[典例引领]
角度一 由空间几何体的直观图识别三视图
(2018·惠州市第三次调研考试)如图所示,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )
【解析】 从几何体的左面看,对角线AD1在视线范围内,画实线,棱C1F不在视线范围内,画虚线.
【答案】 B
角度二 由空间几何体的三视图还原直观图
(2017·高考北京卷)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2
C.2 D.2
【解析】 由三视图还原为如图所示的四棱锥A-BCC1B1,
从图中易得最长的棱长为AC1===2,选B.
【答案】 B
角度三 由空间几何体的部分视图画出剩余部
分视图
(2018·广州市综合测试(一))如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为,则该几何体的俯视图可以是( )
【解析】
由题意可得该几何体可能为四棱锥,如图所示,其高为2,其底面为正方形,面积为2×2=4,因为该几何体的体积为×4×2=,满足条件,所以俯视图可以为一个直角三角形.
【答案】 D
三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的视图.先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.
(2016·高考天津卷)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( )
解析:选B.由几何体的正视图和俯视图可知该几何体为图①,故其侧(左)视图为图②.
空间几何体的直观图
[典例引领]
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6 cm,O′C′=2 cm,则原图形是( )
A.正方形 B.矩形
C.菱形 D.一般的平行四边形
【解析】
如图,在原图形OABC中,
应有OD=2O′D′=2×2=4(cm),
CD=C′D′=2 cm,
所以OC=
==6(cm),
所以OA=OC,
故四边形OABC是菱形,
因此选C.
【答案】 C
若本例中直观图为如图所示的一个边长为1 cm的正方形,则原图形的周长是多少?
解:将直观图还原为平面图形,如图.
可知还原后的图形中OB=2,AB==3,于是周长为2×3+2×1=8(cm).
斜二测画法中的“三变”与“三不变”
“三变”
“三不变”
[通关练习]
1.如图所示为一个平面图形的直观图,则它的实际形状四边形ABCD为( )
A.平行四边形 B.梯形
C.菱形 D.矩形
解析:选D.由斜二测画法可知在原四边形ABCD中DA⊥AB,并且AD∥BC,AB∥CD,故四边形ABCD为矩形.
2.在等腰梯形ABCD中,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为________.
解析:因为OE==1,
所以O′E′=,E′F′=.
所以直观图A′B′C′D′的面积为
S′=×(1+3)×=.
答案:
常见旋转体的三视图
(1)球的三视图都是半径相等的圆.
(2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形.
(3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形.
(4)水平放置的圆柱的正视图和侧视图均为全等的矩形.
根据几何体的三视图判断几何体的结构特征
(1)三视图为三个三角形,一般对应三棱锥;
(2)三视图为两个三角形,一个四边形,一般对应四棱锥;
(3)三视图为两个三角形,一个圆,一般对应圆锥;
(4)三视图为一个三角形,两个四边形,一般对应三棱柱;
(5)三视图为两个四边形,一个圆,一般对应圆柱.
明确三视图与几何体的数量关系
正(主)视图、侧(左)视图的高就是空间几何体的高;正(主)视图、俯视图的长就是空间几何体的最大长度;侧(左)视图、俯视图中的宽就是几何体的最大宽度.
易错防范
(1)台体可以看成是由锥体截得的,易忽视截面与底面平行且侧棱延长后必交于一点.
(2)空间几何体不同放置时其三视图不一定相同.
(3)对于简单组合体,若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,易忽视实虚线的画法.
1.下列说法正确的有( )
①两个面平行且相似,其余各面都是梯形的多面体是棱台;
②经过球面上不同的两点只能作一个大圆;
③各侧面都是正方形的四棱柱一定是正方体;
④圆锥的轴截面是等腰三角形.
A.1个 B.2个
C.3个 D.4个
解析:选A.①中若两个底面平行且相似,其余各面都是梯形,并不能保证侧棱会交于一点,所以①不正确;②中若球面上不同的两点恰为球的某条直径的两个端点,则过此两点的大圆有无数个,所以②不正确;③中底面不一定是正方形,所以③不正确;很明显④是正确的.
2.如图所示是水平放置的三角形的直观图,点D是△ABC的BC边的中点,AB,BC分别与y′轴、x′轴平行,则在原图中三条线段AB,AD,AC中( )
A.最长的是AB,最短的是AC
B.最长的是AC,最短的是AB
C.最长的是AB,最短的是AD
D.最长的是AC,最短的是AD
解析:选B.由条件知,原平面图形中AB⊥BC,从而AB
A.①② B.②③
C.③④ D.①⑤
解析:选D.圆锥的轴截面为等腰三角形,此时①符合条件;
当截面不过旋转轴时,
圆锥的轴截面为双曲线的一支,此时⑤符合条件;
故截面图形可能是①⑤.
4.(2018·惠州市第三次调研考试)某四棱锥的三视图如图所示,则该四棱锥最长棱的棱长为( )
A.1 B.
C. D.2
解析:选C.根据三视图,可知几何体的直观图为如图所示的四棱锥VABCD,其中VB⊥底面ABCD,且底面ABCD是边长为1的正方形,VB=1.所以四棱锥中最长棱为VD.连接BD,易知BD=,在Rt△VBD中,
VD==.
5.(2017·高考全国卷Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A.10 B.12
C.14 D.16
解析:选B.由三视图可知该多面体是一个组合体,下面是一个底面是等腰直角三角形的直三棱柱,上面是一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰长为2,直三棱柱的高为2,三棱锥的高为2,易知该多面体有2个面是梯形,这些梯形的面积之和为×2=12,故选B.
6.有一个长为5 cm,宽为4 cm的矩形,则其直观图的面积为________.
解析:由于该矩形的面积S=5×4=20(cm2),所以其直观图的面积S′=S=5(cm2).
答案:5 cm2
7.如图所示的Rt△ABC绕着它的斜边AB旋转一周得到的图形是________.
解析:过Rt△ABC的顶点C作线段CD⊥AB,垂足为D,所以Rt△ABC绕着它的斜边AB旋转一周后应得到是以CD作为底面圆的半径的两个圆锥的组合体.
答案:两个圆锥的组合体
8.已知某空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有________个.
解析:由三视图知该几何体是一个四棱锥,它的一个侧面与底面垂直,且此侧面的顶点在底面上的射影为对应底边的中点,易知其有两个侧面是直角三角形.
答案:2
9.如图,在四棱锥PABCD中,底面为正方形,PC与底面ABCD垂直,图为该四棱锥的正视图和侧视图,它们是腰长为6 cm的全等的等腰直角三角形.
(1)根据所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求PA.
解:(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形,如图,其面积为36 cm2.
(2)由侧视图可求得PD===6 cm.
由正视图可知AD=6 cm,且AD⊥PD,
所以在Rt△APD中,
PA= = =6 (cm).
10.如图所示,在侧棱长为2的正三棱锥VABC中,∠AVB=∠BVC=∠CVA=40°,过A作截面AEF,求△AEF周长的最小值.
解:如图,将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,则线段AA1的长即为所求△AEF的周长的最小值.
取AA1的中点D,
连接VD,
则VD⊥AA1,∠AVD=60°.
在Rt△VAD中,
AD=VA·sin 60°=3,
所以AA1=2AD=6,
即△AEF周长的最小值为6.
1.某几何体的正视图和侧视图如图(1),它的俯视图的直观图是矩形O1A1B1C1,如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
A.48 B.64
C.96 D.128
解析:选C.由题图(2)及斜二测画法可知原俯视图为如图所示的平行四边形OABC,设CB与y轴的交点为D,则易知CD=2,OD=2×2=4,所以CO==6=OA,所以俯视图是以6为边长的菱形,由三视图知几何体为一个直四棱柱,其高为4,所以该几何体的侧面积为4×6×4=96.故选C.
2.一个三棱锥的正视图和俯视图如图所示,则该三棱锥的侧视图可能为( )
解析:选D.由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,故选D.
3.(2018·福建泉州模拟)某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )
A.圆弧 B.抛物线的一部分
C.椭圆的一部分 D.双曲线的一部分
解析:选D.根据几何体的三视图可得,侧视图中的虚线部分是由平行于旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选D.
4.(2018·广东文雅中学、江西南昌二中联考)某四面体的三视图如图所示,在该四面体的四个面中,直角三角形的面积和是( )
A.2 B.4 C.2+ D.4+2
解析:选C.由三视图可得原几何体如图所示,由三视图知该几何体的高PO=2,底面ABC是边长为2的等腰直角三角形,平面PAC⊥平面ABC,∠ACB=90°,则BC⊥平面PAC,所以BC⊥PC,所以直角三角形有△PBC和△ACB,易求得PC==,又BC=2,所以S△PBC=×2×=,又S△ABC=×2×2=2,所以该四面体的四个面中,直角三角形的面积和为2+,故选C.
5.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.
解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.
(2)直观图如图所示.
6.如图是一个几何体的正视图和俯视图.
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积.
解:(1)正六棱锥.
(2)其侧视图如图:
其中AB=AC,AD⊥BC,
且BC的长是俯视图中的正六边形对边的距离,
即BC=a,
AD的长是正六棱锥的高,即AD=a,
所以该平面图形的面积S=·a·a=a2.
相关资料
更多









