
还剩14页未读,
继续阅读
所属成套资源:2020高考人教A版理科数学一轮复习文档《微点教程》学案
成套系列资料,整套一键下载
2020版《微点教程》高考人教A版理科数学一轮复习文档:第二章第一节 函数及其表示 学案
展开
第二章 函数、导数及其应用
第一节 函数及其表示
2019考纲考题考情
1.函数与映射的概念
2.函数的三要素
函数由定义域、对应关系和值域三个要素构成,对函数y=f(x),x∈A,其中x叫做自变量,x的取值范围A叫做定义域,与x的值对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做值域。
3.函数的表示法
表示函数的常用方法:解析法、列表法、图象法。
4.分段函数
若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数。分段函数虽然由几部分组成,但它表示的是一个函数。
1.一种优先意识
函数定义域是研究函数的基础依据,对函数的研究,必须坚持定义域优先的原则。
2.两个关注点
(1)分段函数是一个函数。
(2)分段函数的定义域、值域是各段定义域、值域的并集。
3.直线x=a(a是常数)与函数y=f(x)的图象有0个或1个交点。
一、走进教材
1.(必修1P18例2改编)下列函数中,与函数y=x+1是相等函数的是( )
A.y=()2 B.y=+1
C.y=+1 D.y=+1
解析 对于A,函数y=()2的定义域为{x|x≥-1},与函数y=x+1的定义域不同,不是相等函数;对于B,定义域和对应法则都相同,是相等函数;对于C,函数y=+1的定义域为{x|x≠0},与函数y=x+1的定义域不同,不是相等函数;对于D,定义域相同,但对应法则不同,不是相等函数。故选B。
答案 B
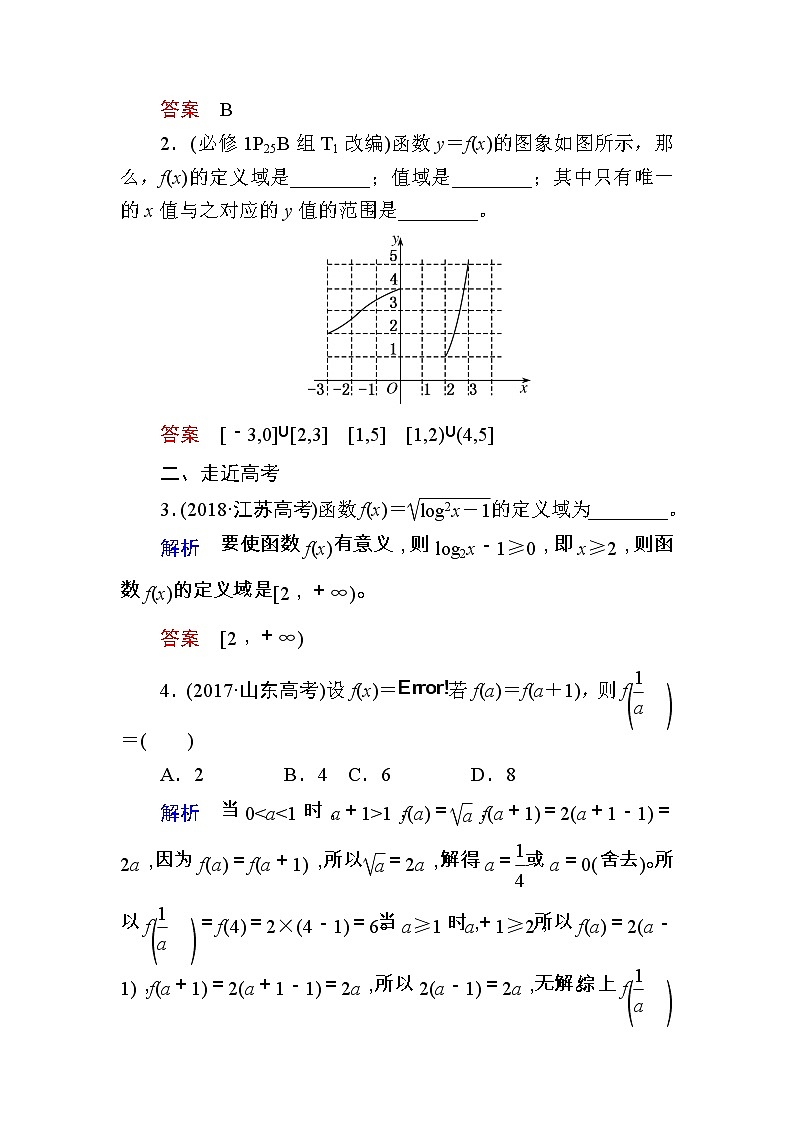
2.(必修1P25B组T1改编)函数y=f(x)的图象如图所示,那么,f(x)的定义域是________;值域是________;其中只有唯一的x值与之对应的y值的范围是________。
答案 [-3,0]∪[2,3] [1,5] [1,2)∪(4,5]
二、走近高考
3.(2018·江苏高考)函数f(x)=的定义域为________。
解析 要使函数f(x)有意义,则log2x-1≥0,即x≥2,则函数f(x)的定义域是[2,+∞)。
答案 [2,+∞)
4.(2017·山东高考)设f(x)=若f(a)=f(a+1),则f=( )
A.2 B.4 C.6 D.8
解析 当01,f(a)=,f(a+1)=2(a+1-1)=2a,因为f(a)=f(a+1),所以=2a,解得a=或a=0(舍去)。所以f=f(4)=2×(4-1)=6。当a≥1时,a+1≥2,所以f(a)=2(a-1),f(a+1)=2(a+1-1)=2a,所以2(a-1)=2a,无解。综上f=6。故选C。
解析:由f(x)的解析式可知其图象如图所示,f(x)的定义域为(0,+∞),f(x)在(0,1)上单调递增,在[1,+∞)上单调递增。由f(a)=f(a+1)可知,自变量a和a+1不可能同在单调区间(0,1)上,自变量a和a+1也不可能同在单调区间[1,+∞)上,因此自变量a和a+1必须分别分布在两个不同的区间上。又a
答案 C
三、走出误区
微提醒:①对函数概念理解不透彻;②对分段函数解不等式时忘记范围;③换元法求解析式,反解忽视范围。
5.已知集合P={x|0≤x≤4},Q={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是________。(填序号)
①f:x→y=x;②f:x→y=x;③f:x→y=x;④f:x→y=。
解析 对于③,因为当x=4时,y=×4=∉Q,所以③不是函数。
答案 ③
6.设函数f(x)=则使得f(x)≥1的自变量x的取值范围为________。
解析 因为f(x)是分段函数,所以f(x)≥1应分段求解。当x<1时,f(x)≥1⇒(x+1)2≥1⇒x≤-2或x≥0,所以x≤-2或0≤x<1。当x≥1时,f(x)≥1⇒4-≥1,即≤3,所以1≤x≤10。综上所述,x≤-2或0≤x≤10,即x∈(-∞,-2]∪[0,10]。
答案 (-∞,-2]∪[0,10]
7.已知f()=x-1,则f(x)=________。
解析 令t=,则t≥0,x=t2,所以f(t)=t2-1(t≥0),即f(x)=x2-1(x≥0)。
答案 x2-1(x≥0)
考点一 函数的定义域
【例1】 (1)(2019·河南、河北两省重点高中联考)函数f(x)=+ln(x+4)的定义域为________。
(2)已知函数y=f(x)的定义域为[-8,1],则函数g(x)=的定义域是________。
解析 (1)要使函数f(x)有意义,需有解得-4
答案 (1)(-4,1] (2)∪(-2,0]
1.求给定函数的定义域往往转化为解不等式(组)的问题,可借助于数轴,注意端点值的取舍。
2.求抽象函数的定义域:①若y=f(x)的定义域为(a,b),则解不等式a
A.(-∞,-4]∪[2,+∞)
B.(-4,0)∪(0,1)
C.[-4,0)∪(0,1)
D.[-4,0)∪(0,1]
(2)若函数y=f(x)的定义域是[0,2 018],则函数g(x)=的定义域是( )
A.[-1,2 017] B.[-1,1)∪(1,2 017]
C.[0,2 018] D.[-1,1)∪(1,2 018]
(3)若函数f(x)=的定义域为{x|1≤x≤2},则a+b的值为________。
解析 (1)由解得-4≤x<0或0
答案 (1)C (2)B (3)-
考点二 求函数的解析式
【例2】 (1)已知二次函数f(x)满足f(2x+1)=4x2-6x+5,则f(x)=________。
(2)已知f(x)满足2f(x)+f=3x,则f(x)=________。
(3)定义在R上的函数f(x)满足f(x+1)=2f(x)。若当0≤x≤1时,f(x)=x(1-x),则当-1≤x<0时,f(x)=________。
解析 (1)令2x+1=t(t∈R),则x=,所以f(t)=42-6×+5=t2-5t+9(t∈R),所以f(x)=x2-5x+9(x∈R)。
解法一(配凑法):因为f(2x+1)=4x2-6x+5=(2x+1)2-10x+4=(2x+1)2-5(2x+1)+9,所以f(x)=x2-5x+9。
解法二(待定系数法):因为f(x)是二次函数,所以设f(x)=ax2+bx+c(a≠0),则f(2x+1)=a(2x+1)2+b(2x+1)+c=4ax2+(4a+2b)x+a+b+c。因为f(2x+1)=4x2-6x+5,所以解得所以f(x)=x2-5x+9。
(2)因为2f(x)+f=3x ①,所以将x用替换,得2f+f(x)= ②,由①②解得f(x)=2x-(x≠0),即f(x)的解析式是f(x)=2x-(x≠0)。
(3)(转换法)当-1≤x<0时,则0≤x+1<1,故f(x+1)=(x+1)(1-x-1)=-x(x+1),又f(x+1)=2f(x),所以-1≤x<0时,f(x)=-。
答案 (1)x2-5x+9 (2)2x-(x≠0)
(3)-
求函数解析式常用到如下方法
①待定系数法;②换元法;③配凑法;④转换法;⑤解方程组法。
【变式训练】 (1)已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,则f(x)=________。
(2)已知f=lgx,则f(x)=________。
解析 (1)设f(x)=ax2+bx+c(a≠0),由f(0)=0,知c=0,f(x)=ax2+bx。又由f(x+1)=f(x)+x+1,得a(x+1)2+b(x+1)=ax2+bx+x+1,即ax2+(2a+b)x+a+b=ax2+(b+1)x+1,所以解得a=b=。所以f(x)=x2+x(x∈R)。
(2)令+1=t得x=,代入得f(t)=lg,又x>0,所以t>1,故f(x)的解析式是f(x)=lg(x>1)。
答案 (1)x2+x(x∈R) (2)lg(x>1)
考点三 分段函数微点小专题
方向1:分段函数求值
【例3】 (2018·江苏高考)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(-2,2]上,f(x)=则f(f(15))的值为________。
解析 因为函数f(x)满足f(x+4)=f(x)(x∈R),所以函数f(x)的最小正周期是4。因为在区间(-2,2]上,f(x)=所以f(f(15))=f(f(-1))=f=cos=。
答案
根据分段函数解析式求函数值。首先确定自变量的值属于哪个区间,其次选定相应的解析式代入求解,同时也要注意函数的奇偶性、周期性的应用。
方向2:求参数或自变量的值
【例4】 已知f(x)=不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
A.(-∞,-2) B.(-∞,0)
C.(0,2) D.(-2,0)
解析 二次函数f(x)=x2-4x+3的对称轴是x=2,所以该函数在(-∞,0]上单调递减,所以x2-4x+3≥3,同理f(x)=-x2-2x+3在(0,+∞)上单调递减,所以-x2-2x+3<3。所以f(x)在R上单调递减,所以由f(x+a)>f(2a-x)得x+a<2a-x,即2x
此类问题有以下两种解法
1.解决此类问题时,先在分段函数的各段上分别求解,然后将求出的值或范围与该段函数的自变量的取值范围求交集,最后将各段的结果合起来(取并集)即可。
2.如果分段函数的图象易得,也可以画出函数图象后结合图象求解。
【题点对应练】
1.(方向1)已知f(x)=(0
C.3 D.-3
解析 由题意得,f(-2)=a-2+b=5 ①,f(-1)=a-1+b=3 ②,联立①②,结合0
2.(方向2)设函数f(x)=则满足f(f(a))=2f(a)的a的取值范围是( )
A. B.[0,1]
C. D.[1,+∞)
解析 由已知函数和f(f(a))=2f(a),得f(a)≥1。若a<1,则3a-1≥1,解得a≥,此时≤a<1;若a≥1,则2a≥1,解得a≥0,此时a≥1,综上可知a≥,即a的取值范围是。
答案 C
考点四 函数新定义问题
【例5】 (2019·洛阳高三统考)若函数f(x)同时满足下列两个条件,则称该函数为“优美函数”:
(1)∀x∈R,都有f(-x)+f(x)=0;
(2)∀x1,x2∈R,且x1≠x2,都有<0。
①f(x)=sinx;②f(x)=-2x3;③f(x)=1-x;④f(x)=ln(+x)。
以上四个函数中,“优美函数”的个数是( )
A.0 B.1
C.2 D.3
解析 由条件(1),得f(x)是R上的奇函数,由条件(2),得f(x)是R上的单调递减函数。对于①,f(x)=sinx在R上不单调,故不是“优美函数”;对于②,f(x)=-2x3既是奇函数,又在R上单调递减,故是“优美函数”;对于③,f(x)=1-x不是奇函数,故不是“优美函数”;对于④,易知f(x)在R上单调递增,故不是“优美函数”。故选B。
答案 B
所谓“新定义”函数,是相对于高中教材而言,指在高中教材中不曾出现过或尚未介绍的一类函数。函数新定义问题的一般形式是:由命题者先给出一个新的概念、新的运算法则,或者给出一个抽象函数的性质等,然后让学生按照这种“新定义”去解决相关的问题。常见形式有:①讨论新函数的性质;②利用新函数进行运算;③判断新函数的图象;④利用新概念判断命题真假等。
【变式训练】 若函数y=f(x)的图象上存在不同的两点M,N关于原点对称,则称点对(M,N)是函数y=f(x)的一对“和谐点对”。已知函数f(x)=则此函数的“和谐点对”有( )
A.1对 B.2对
C.3对 D.4对
解析 作出函数f(x)=的图象如图所示,f(x)的“和谐点对”数可转化为y=ex(x<0)和y=-x2-4x(x<0)的图象的交点个数。由图象知,函数f(x)有2对“和谐点对”。
答案 B
1.(配合例1使用)已知集合M是函数y=的定义域,集合N是函数y=x2-4的值域,则M∩N=( )
A.
B.
C.
D.∅
解析 由题意得M=,N=[-4,+∞),所以M∩N=。故选B。
答案 B
2.(配合例2使用)已知f=+,则f(x)=( )
A.(x+1)2 (x≠1) B.(x-1)2 (x≠1)
C.x2-x+1 (x≠1) D.x2+x+1 (x≠1)
解析 f=+=2-+1,令t=,因为=+1≠1,所以t≠1,所以f(t)=t2-t+1(t≠1),所以f(x)=x2-x+1(x≠1)。故选C。
答案 C
3.(配合例3使用)已知函数f(x)=则f的值为( )
A.-1 B.1
C. D.
解析 依题意得f=f+1=f+1+1=2cos+2=2×+2=1。故选B。
答案 B
4.(配合例4使用)设函数f(x)=则满足f(x)+f>1的x的取值范围是________。
解析 根据分段函数的性质分情况讨论,当x≤0时,则f(x)+f=x+1+x-+1>1,解得-0时,根据指数函数的图象和性质以及一次函数的性质与图象可得,f(x)+f>1恒成立,所以x的取值范围是。
答案
5.(配合例5使用)数学上称函数y=kx+b(k,b∈R,k≠0)为线性函数。对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+f′(x0)(x-x0)。利用这一方法,m=的近似代替值( )
A.大于m
B.小于m
C.等于m
D.与m的大小关系无法确定
解析 依题意,取f(x)=,则f′(x)=,所以≈+(x-x0)。令x=4.001,x0=4,所以≈2+×0.001。因为2=4+0.001+2>4.001,所以m=的近似代替值大于m。
答案 A
换元法求函数值
函数求值问题涉及很多方面:
1.分段函数求值问题,关键在于准确确定与自变量对应的函数解析式。
2.利用函数性质求值的关键在于利用函数的奇偶性、周期性或对称性等将自变量转化到已知区间内求解。
3.对于自变量之间存在某种特殊关系的函数求值问题,要注意与自变量对应的函数值之间关系的建立。
这里我们重点研究换元法求函数值,请看下面例子:
【典例】 设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f(f(x)-ex)=e+1(e是自然对数的底数),则f(ln2)的值等于( )
A.1 B.2
C.3 D.4
【解析】 因为f(x)为单调递增函数,且对任意实数x,都有f(f(x)-ex)=e+1,所以f(x)-ex必然是一个常数,设f(x)-ex=t(t为常数),则f(x)=ex+t,故f(t)=et+t。由已知可得f(t)=e+1,所以et+t=e+1。又函数y=ex+x在R上是单调递增的,显然t=1,所以f(x)=ex+1,故f(ln2)=eln2+1=3。故选C。
【答案】 C
先利用换元法,根据已知求出函数f(x)的解析式,然后代入求值。
【变式训练】 设定义在R上的函数f(x)满足f(tan2x)=,则f+f+…+f+f+f(0)+f(2)+f(3)+…+f(2 016)+f(2 017)=________。
解析 设t=tan2x,则====,所以f(t)=。故f(t)+f=+=+=0。所以f+f+…+f+f+f(0)+f(2)+f(3)+…+f(2 016)+f(2 017)=f(0)==1。
答案 1
第一节 函数及其表示
2019考纲考题考情
1.函数与映射的概念
2.函数的三要素
函数由定义域、对应关系和值域三个要素构成,对函数y=f(x),x∈A,其中x叫做自变量,x的取值范围A叫做定义域,与x的值对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做值域。
3.函数的表示法
表示函数的常用方法:解析法、列表法、图象法。
4.分段函数
若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数。分段函数虽然由几部分组成,但它表示的是一个函数。
1.一种优先意识
函数定义域是研究函数的基础依据,对函数的研究,必须坚持定义域优先的原则。
2.两个关注点
(1)分段函数是一个函数。
(2)分段函数的定义域、值域是各段定义域、值域的并集。
3.直线x=a(a是常数)与函数y=f(x)的图象有0个或1个交点。
一、走进教材
1.(必修1P18例2改编)下列函数中,与函数y=x+1是相等函数的是( )
A.y=()2 B.y=+1
C.y=+1 D.y=+1
解析 对于A,函数y=()2的定义域为{x|x≥-1},与函数y=x+1的定义域不同,不是相等函数;对于B,定义域和对应法则都相同,是相等函数;对于C,函数y=+1的定义域为{x|x≠0},与函数y=x+1的定义域不同,不是相等函数;对于D,定义域相同,但对应法则不同,不是相等函数。故选B。
答案 B
2.(必修1P25B组T1改编)函数y=f(x)的图象如图所示,那么,f(x)的定义域是________;值域是________;其中只有唯一的x值与之对应的y值的范围是________。
答案 [-3,0]∪[2,3] [1,5] [1,2)∪(4,5]
二、走近高考
3.(2018·江苏高考)函数f(x)=的定义域为________。
解析 要使函数f(x)有意义,则log2x-1≥0,即x≥2,则函数f(x)的定义域是[2,+∞)。
答案 [2,+∞)
4.(2017·山东高考)设f(x)=若f(a)=f(a+1),则f=( )
A.2 B.4 C.6 D.8
解析 当0
解析:由f(x)的解析式可知其图象如图所示,f(x)的定义域为(0,+∞),f(x)在(0,1)上单调递增,在[1,+∞)上单调递增。由f(a)=f(a+1)可知,自变量a和a+1不可能同在单调区间(0,1)上,自变量a和a+1也不可能同在单调区间[1,+∞)上,因此自变量a和a+1必须分别分布在两个不同的区间上。又a
答案 C
三、走出误区
微提醒:①对函数概念理解不透彻;②对分段函数解不等式时忘记范围;③换元法求解析式,反解忽视范围。
5.已知集合P={x|0≤x≤4},Q={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是________。(填序号)
①f:x→y=x;②f:x→y=x;③f:x→y=x;④f:x→y=。
解析 对于③,因为当x=4时,y=×4=∉Q,所以③不是函数。
答案 ③
6.设函数f(x)=则使得f(x)≥1的自变量x的取值范围为________。
解析 因为f(x)是分段函数,所以f(x)≥1应分段求解。当x<1时,f(x)≥1⇒(x+1)2≥1⇒x≤-2或x≥0,所以x≤-2或0≤x<1。当x≥1时,f(x)≥1⇒4-≥1,即≤3,所以1≤x≤10。综上所述,x≤-2或0≤x≤10,即x∈(-∞,-2]∪[0,10]。
答案 (-∞,-2]∪[0,10]
7.已知f()=x-1,则f(x)=________。
解析 令t=,则t≥0,x=t2,所以f(t)=t2-1(t≥0),即f(x)=x2-1(x≥0)。
答案 x2-1(x≥0)
考点一 函数的定义域
【例1】 (1)(2019·河南、河北两省重点高中联考)函数f(x)=+ln(x+4)的定义域为________。
(2)已知函数y=f(x)的定义域为[-8,1],则函数g(x)=的定义域是________。
解析 (1)要使函数f(x)有意义,需有解得-4
答案 (1)(-4,1] (2)∪(-2,0]
1.求给定函数的定义域往往转化为解不等式(组)的问题,可借助于数轴,注意端点值的取舍。
2.求抽象函数的定义域:①若y=f(x)的定义域为(a,b),则解不等式a
A.(-∞,-4]∪[2,+∞)
B.(-4,0)∪(0,1)
C.[-4,0)∪(0,1)
D.[-4,0)∪(0,1]
(2)若函数y=f(x)的定义域是[0,2 018],则函数g(x)=的定义域是( )
A.[-1,2 017] B.[-1,1)∪(1,2 017]
C.[0,2 018] D.[-1,1)∪(1,2 018]
(3)若函数f(x)=的定义域为{x|1≤x≤2},则a+b的值为________。
解析 (1)由解得-4≤x<0或0
答案 (1)C (2)B (3)-
考点二 求函数的解析式
【例2】 (1)已知二次函数f(x)满足f(2x+1)=4x2-6x+5,则f(x)=________。
(2)已知f(x)满足2f(x)+f=3x,则f(x)=________。
(3)定义在R上的函数f(x)满足f(x+1)=2f(x)。若当0≤x≤1时,f(x)=x(1-x),则当-1≤x<0时,f(x)=________。
解析 (1)令2x+1=t(t∈R),则x=,所以f(t)=42-6×+5=t2-5t+9(t∈R),所以f(x)=x2-5x+9(x∈R)。
解法一(配凑法):因为f(2x+1)=4x2-6x+5=(2x+1)2-10x+4=(2x+1)2-5(2x+1)+9,所以f(x)=x2-5x+9。
解法二(待定系数法):因为f(x)是二次函数,所以设f(x)=ax2+bx+c(a≠0),则f(2x+1)=a(2x+1)2+b(2x+1)+c=4ax2+(4a+2b)x+a+b+c。因为f(2x+1)=4x2-6x+5,所以解得所以f(x)=x2-5x+9。
(2)因为2f(x)+f=3x ①,所以将x用替换,得2f+f(x)= ②,由①②解得f(x)=2x-(x≠0),即f(x)的解析式是f(x)=2x-(x≠0)。
(3)(转换法)当-1≤x<0时,则0≤x+1<1,故f(x+1)=(x+1)(1-x-1)=-x(x+1),又f(x+1)=2f(x),所以-1≤x<0时,f(x)=-。
答案 (1)x2-5x+9 (2)2x-(x≠0)
(3)-
求函数解析式常用到如下方法
①待定系数法;②换元法;③配凑法;④转换法;⑤解方程组法。
【变式训练】 (1)已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,则f(x)=________。
(2)已知f=lgx,则f(x)=________。
解析 (1)设f(x)=ax2+bx+c(a≠0),由f(0)=0,知c=0,f(x)=ax2+bx。又由f(x+1)=f(x)+x+1,得a(x+1)2+b(x+1)=ax2+bx+x+1,即ax2+(2a+b)x+a+b=ax2+(b+1)x+1,所以解得a=b=。所以f(x)=x2+x(x∈R)。
(2)令+1=t得x=,代入得f(t)=lg,又x>0,所以t>1,故f(x)的解析式是f(x)=lg(x>1)。
答案 (1)x2+x(x∈R) (2)lg(x>1)
考点三 分段函数微点小专题
方向1:分段函数求值
【例3】 (2018·江苏高考)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(-2,2]上,f(x)=则f(f(15))的值为________。
解析 因为函数f(x)满足f(x+4)=f(x)(x∈R),所以函数f(x)的最小正周期是4。因为在区间(-2,2]上,f(x)=所以f(f(15))=f(f(-1))=f=cos=。
答案
根据分段函数解析式求函数值。首先确定自变量的值属于哪个区间,其次选定相应的解析式代入求解,同时也要注意函数的奇偶性、周期性的应用。
方向2:求参数或自变量的值
【例4】 已知f(x)=不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
A.(-∞,-2) B.(-∞,0)
C.(0,2) D.(-2,0)
解析 二次函数f(x)=x2-4x+3的对称轴是x=2,所以该函数在(-∞,0]上单调递减,所以x2-4x+3≥3,同理f(x)=-x2-2x+3在(0,+∞)上单调递减,所以-x2-2x+3<3。所以f(x)在R上单调递减,所以由f(x+a)>f(2a-x)得x+a<2a-x,即2x
此类问题有以下两种解法
1.解决此类问题时,先在分段函数的各段上分别求解,然后将求出的值或范围与该段函数的自变量的取值范围求交集,最后将各段的结果合起来(取并集)即可。
2.如果分段函数的图象易得,也可以画出函数图象后结合图象求解。
【题点对应练】
1.(方向1)已知f(x)=(0
C.3 D.-3
解析 由题意得,f(-2)=a-2+b=5 ①,f(-1)=a-1+b=3 ②,联立①②,结合0
2.(方向2)设函数f(x)=则满足f(f(a))=2f(a)的a的取值范围是( )
A. B.[0,1]
C. D.[1,+∞)
解析 由已知函数和f(f(a))=2f(a),得f(a)≥1。若a<1,则3a-1≥1,解得a≥,此时≤a<1;若a≥1,则2a≥1,解得a≥0,此时a≥1,综上可知a≥,即a的取值范围是。
答案 C
考点四 函数新定义问题
【例5】 (2019·洛阳高三统考)若函数f(x)同时满足下列两个条件,则称该函数为“优美函数”:
(1)∀x∈R,都有f(-x)+f(x)=0;
(2)∀x1,x2∈R,且x1≠x2,都有<0。
①f(x)=sinx;②f(x)=-2x3;③f(x)=1-x;④f(x)=ln(+x)。
以上四个函数中,“优美函数”的个数是( )
A.0 B.1
C.2 D.3
解析 由条件(1),得f(x)是R上的奇函数,由条件(2),得f(x)是R上的单调递减函数。对于①,f(x)=sinx在R上不单调,故不是“优美函数”;对于②,f(x)=-2x3既是奇函数,又在R上单调递减,故是“优美函数”;对于③,f(x)=1-x不是奇函数,故不是“优美函数”;对于④,易知f(x)在R上单调递增,故不是“优美函数”。故选B。
答案 B
所谓“新定义”函数,是相对于高中教材而言,指在高中教材中不曾出现过或尚未介绍的一类函数。函数新定义问题的一般形式是:由命题者先给出一个新的概念、新的运算法则,或者给出一个抽象函数的性质等,然后让学生按照这种“新定义”去解决相关的问题。常见形式有:①讨论新函数的性质;②利用新函数进行运算;③判断新函数的图象;④利用新概念判断命题真假等。
【变式训练】 若函数y=f(x)的图象上存在不同的两点M,N关于原点对称,则称点对(M,N)是函数y=f(x)的一对“和谐点对”。已知函数f(x)=则此函数的“和谐点对”有( )
A.1对 B.2对
C.3对 D.4对
解析 作出函数f(x)=的图象如图所示,f(x)的“和谐点对”数可转化为y=ex(x<0)和y=-x2-4x(x<0)的图象的交点个数。由图象知,函数f(x)有2对“和谐点对”。
答案 B
1.(配合例1使用)已知集合M是函数y=的定义域,集合N是函数y=x2-4的值域,则M∩N=( )
A.
B.
C.
D.∅
解析 由题意得M=,N=[-4,+∞),所以M∩N=。故选B。
答案 B
2.(配合例2使用)已知f=+,则f(x)=( )
A.(x+1)2 (x≠1) B.(x-1)2 (x≠1)
C.x2-x+1 (x≠1) D.x2+x+1 (x≠1)
解析 f=+=2-+1,令t=,因为=+1≠1,所以t≠1,所以f(t)=t2-t+1(t≠1),所以f(x)=x2-x+1(x≠1)。故选C。
答案 C
3.(配合例3使用)已知函数f(x)=则f的值为( )
A.-1 B.1
C. D.
解析 依题意得f=f+1=f+1+1=2cos+2=2×+2=1。故选B。
答案 B
4.(配合例4使用)设函数f(x)=则满足f(x)+f>1的x的取值范围是________。
解析 根据分段函数的性质分情况讨论,当x≤0时,则f(x)+f=x+1+x-+1>1,解得-
答案
5.(配合例5使用)数学上称函数y=kx+b(k,b∈R,k≠0)为线性函数。对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+f′(x0)(x-x0)。利用这一方法,m=的近似代替值( )
A.大于m
B.小于m
C.等于m
D.与m的大小关系无法确定
解析 依题意,取f(x)=,则f′(x)=,所以≈+(x-x0)。令x=4.001,x0=4,所以≈2+×0.001。因为2=4+0.001+2>4.001,所以m=的近似代替值大于m。
答案 A
换元法求函数值
函数求值问题涉及很多方面:
1.分段函数求值问题,关键在于准确确定与自变量对应的函数解析式。
2.利用函数性质求值的关键在于利用函数的奇偶性、周期性或对称性等将自变量转化到已知区间内求解。
3.对于自变量之间存在某种特殊关系的函数求值问题,要注意与自变量对应的函数值之间关系的建立。
这里我们重点研究换元法求函数值,请看下面例子:
【典例】 设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f(f(x)-ex)=e+1(e是自然对数的底数),则f(ln2)的值等于( )
A.1 B.2
C.3 D.4
【解析】 因为f(x)为单调递增函数,且对任意实数x,都有f(f(x)-ex)=e+1,所以f(x)-ex必然是一个常数,设f(x)-ex=t(t为常数),则f(x)=ex+t,故f(t)=et+t。由已知可得f(t)=e+1,所以et+t=e+1。又函数y=ex+x在R上是单调递增的,显然t=1,所以f(x)=ex+1,故f(ln2)=eln2+1=3。故选C。
【答案】 C
先利用换元法,根据已知求出函数f(x)的解析式,然后代入求值。
【变式训练】 设定义在R上的函数f(x)满足f(tan2x)=,则f+f+…+f+f+f(0)+f(2)+f(3)+…+f(2 016)+f(2 017)=________。
解析 设t=tan2x,则====,所以f(t)=。故f(t)+f=+=+=0。所以f+f+…+f+f+f(0)+f(2)+f(3)+…+f(2 016)+f(2 017)=f(0)==1。
答案 1
相关资料
更多








