初中数学人教版九年级下册28.1 锐角三角函数评课课件ppt

这是一份初中数学人教版九年级下册28.1 锐角三角函数评课课件ppt，共53页。PPT课件主要包含了勾股定理，精讲点拨，探究2，探究3，尝试练习，探究4，探究5，探究6，构造直角三角形，拓展应用新知等内容，欢迎下载使用。

如图：在Rt △ABC中，∠C＝90°，
角：∠A+ ∠B ＝90°
边：AC2 + BC2 = AB2
在直角三角形中，边与角之间有什么关系呢？
在直角三角形中，边之间有什么关系？角之间有什么关系呢？
1.理解当直角三角形的锐角固定时，它的对边与斜边的比值就固定（即正弦值不变）这一事实.2.理解正弦的概念.
问题：为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌．现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为35m，那么需要准备多长的水管？
分析：这个问题可以归结为，在Rt△ABC中，∠C＝90°，∠A＝30°,BC＝35m，求AB.
在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝35，求AB。
根据：“在直角三角形中， 30°角所对的边等于斜边的一半”
可得AB＝2BC＝70米
也就是说需要准备70米长的水管
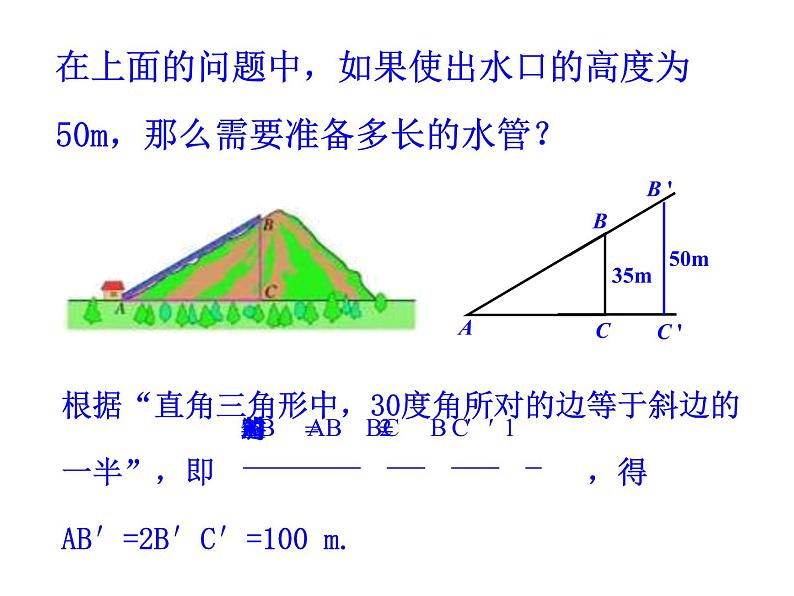
在上面的问题中，如果使出水口的高度为50m，那么需要准备多长的水管？
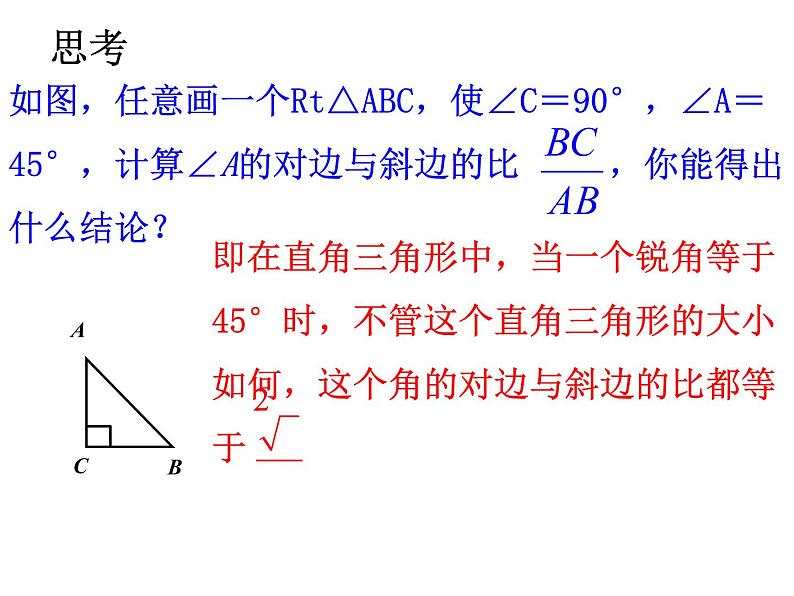
即在直角三角形中，当一个锐角等于45°时，不管这个直角三角形的大小如何，这个角的对边与斜边的比都等于
如图，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计算∠A的对边与斜边的比 ，你能得出什么结论？
综上可知，在一个Rt△ABC中，∠C＝90°，当∠A＝30°时，∠A的对边与斜边的比都等于 ，是一个固定值；当∠A＝45°时，∠A的对边与斜边的比都等于 ，也是一个固定值.
一般地，当∠A 取其他一定度数的锐角时，它的对边与斜边的比是否也是一个固定值？
任意画Rt△ABC和Rt△A′B′C′，使得∠C＝∠C′＝90°，∠A＝∠A′＝α，那么 与 有什么关系．你能解释一下吗？
两个三角形相似，对应边成比例，故比值相等.
这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比都是一个固定值．
如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，记作sin A．即
例如，当∠A＝30°时，我们有
当∠A＝45°时，我们有
一般地,在Rt△ABC中，∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:
sin A=
∠B的正弦如何表示呢?
(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积 (3) sinA 是一个比值 (4)sinA 没有单位
对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.
sinA = sin30°=
sinA = sin45°=
sinA = sin60°=
与所在三角形大小无关，只与度数有关
思考：1、锐角A的正弦值可以等于1吗？为什么？
对于锐角A的每一个确定的值，sinA有唯一的确定的值与它对应，所以sinA是A的函数。
3、不同大小的两个锐角的正弦值可能相等吗？
对于锐角A的每一个确定的值，sinA有唯一的确定的值与它对应，反之，已知 sinA的值可求出角A的度数。
锐角A满足2sin（A－15 °）＝1，那么∠A＝____.
sinA是一个比值（注意比的顺序），无单位；
2.在Rt△ABC中，锐角A的对边和斜边同时扩大 100倍，sinA的值（ ） A.扩大100倍 B.缩小 C.不变 D.不能确定
4、如图，P为角a的一边OA上的任一点，过P作PQ ⊥OB于点Q，则a的正弦函数值与( )A、角a的大小无关 B、点P的位位置无关C、角a的度数无关 D、OP的长度有关
5、判断：Rt △ABC中，∠C＝90°，sinA= ，则 a = 4，c = 5 。（ ）
6.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5求sinA和sinB的值.
解:在Rt △ABC中,
能够成为直角三角形三条边长的三个正整数，称为勾股数.
3、4、____5、12、___6、8、___7、24、____8、15、___9、12、___3k、4k、____
7、如图，∠C=900，AB= ，BC= ，求∠A的度数。
【例1】如图，在Rt△ABC中,∠B=90°,AC=200,sin A=0.6，求BC的长.
【解析】在Rt△ABC中,
已知锐角的正弦值求三角形的边长
　　 【例2】（1）在△ABC中，∠C=90°，BC=2，sin A= ，则边AC的长是（ ）A． B.3 C. D.13（2）在△ABC中，∠C=90°，AC=2，sin A= ，则边BC的长是______.
【自主解答】（1）选A．∵sin A= ，BC=2，∴AB=3．∴（2）∵sin A= ，设BC的长为2k，∴AB=5k．则(2k)2+22=(5k)2，解得答案:
正弦定义中已知二个量，可求其它量
1.在△ABC中，∠C＝90°，BC＝6 cm，sin A＝ 则AB的长是（ ）A.3 cm B.4 cm C.5 cm D.10 cm【解析】选D.在Rt△ACB中，BC＝6 cm，sin A＝∴AB＝10 cm．
2.在△ABC中，∠C＝90°，BC＝9 cm，sin B＝ ，则AB的长是_______.【解析】∵∠C＝90°，sin B＝ ，∴ ,设AC为4k，AB为5k，则 ，∴3k=9 cm，∴k=3 cm，∴5k=15 cm.答案:15 cm
3.如图，在Rt△ACB中，∠C=90°，sin A= ，AB=15，求△ABC的周长．【解析】在Rt△ACB中, ∠C=90°,AB=15,∵sin A=∴BC=12，∴△ABC的周长为15+12+9=36.
.如图, ∠C=90°CD⊥AB.sin B可以用哪两条线段之比表示?
若ＡC=5,CD=3,求sin B的值.
【解析】sinB可以用 或 或
求一个角的正弦值，除了用定义直接求外，还可以转化为求和它相等角的正弦值。
　　如图, ∠C=90°CD⊥AB.sinB可以由哪两条线段之比?
若ＡC=5,CD=3,求sinB的值.
解: ∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中，AD=
【想一想错在哪？】在Rt△ABC中，AC=3,BC=4.求较大角的正弦值.提示:漏掉了BC为斜边，∠A为直角的情况！
1.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.
2.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.
1.把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值（ ）A．不变B．缩小为原来的C．扩大为原来的3倍D．不能确定
2.(2013·温州中考)如图，在△ABC中，∠C=90°，AB=5，BC=3，则sin A的值是( )A. B.C. D. 【解析】选C.sin A=
3.三角形在正方形网格纸中的位置如图所示．则sin α的值是 （ ）A. B. C. D.
【方法技巧】网格中求三角函数的三步骤1.在网格中求锐角的三角函数常将小正方形的边长设为单位“1”.2.根据勾股定理求得三角形的各边长.3.根据三角函数的概念求解.
4.如图，在Rt△ACB中，∠C＝90°，AB＝2BC，则sin B的值（ ）A． B． C． D．1
5.如图，角α的顶点为O，它的一边在x轴的正半轴上，另一边OA上有一点P（3，4），则sin α＝_________．
6.在Rt△ABC中，∠C=90°，a，b，c分别是∠A，∠B，∠C的对边，若2a= c，则∠A的正弦值等于______.【解析】由正弦的概念可知，sin A=答案:
7.在Rt△ABC中，∠C=90°，AB=13，sin A= ，求△ABC的面积是多少？【解析】∵sin A=∴BC= AB= ×13=5，∴∴S△ABC = AC·BC= ×12×5=30.
8、在平面直角坐标系中，有一条直线l： ，l与x轴的正半轴的夹角为α，求sinα的值。
1.在△ABC中,∠C=900,sinA+sinB=,AC+BC=28,求AB的长.
2、如图，在△ABC中， AB=BC=5，sinA= ，求△ABC 的面积。
3.已知在RT△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=AE=7,求DE的长.
要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?
1.锐角三角函数定义:
2.sinA是∠A的函数.
3.只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.
谢谢各位老师光临指导!
1、根据下图，求sinA和sinB的值．
2.在平面直角坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____.3.在Rt△ABC中,∠C=90°,AD是BC边上的中线,AC=2,BC=4,则sin∠DAC=_____.4.如图,在Rt△ABC中, 则sin A=___.