


所属成套资源:人教版(五四制)数学九年级下册PPT课件全册(含复习课件)
人教版 (五四制)九年级下册33.3 位似优质ppt课件
展开
这是一份人教版 (五四制)九年级下册33.3 位似优质ppt课件,共29页。PPT课件主要包含了学习目标,情境引入,上面图片有什么特征,相似图形,合作探究,还有其他画法吗,总结归纳,典例精析,小试牛刀,课堂检测等内容,欢迎下载使用。
1.掌握位似图形的概念、性质和画法. 2.掌握位似与相似的联系与区别. 3.理解平面直角坐标系中,位似图形对应点的坐标之间的联系.4.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律. 5.了解四种图形变换 (平移、轴对称旋转和位似) 的异同,并能在复杂图形中找出这些变换.
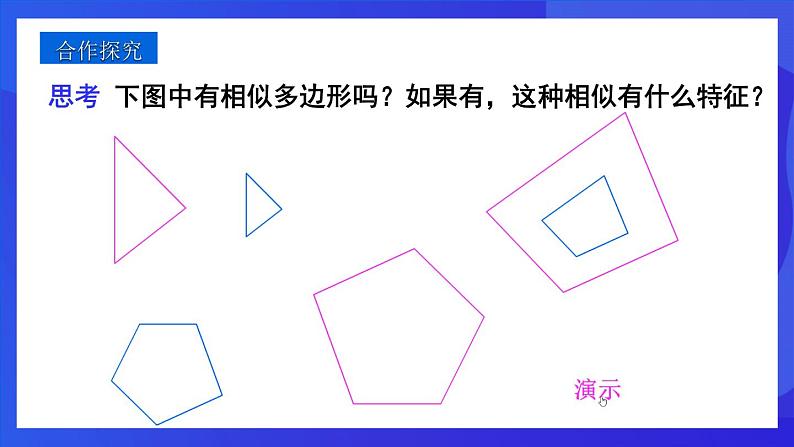
思考 下图中有相似多边形吗?如果有,这种相似有什么特征?
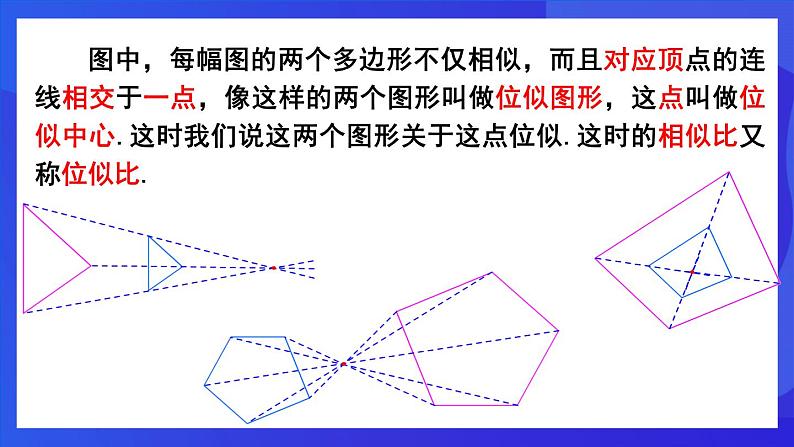
图中,每幅图的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这点叫做位似中心.这时我们说这两个图形关于这点位似.这时的相似比又称位似比.
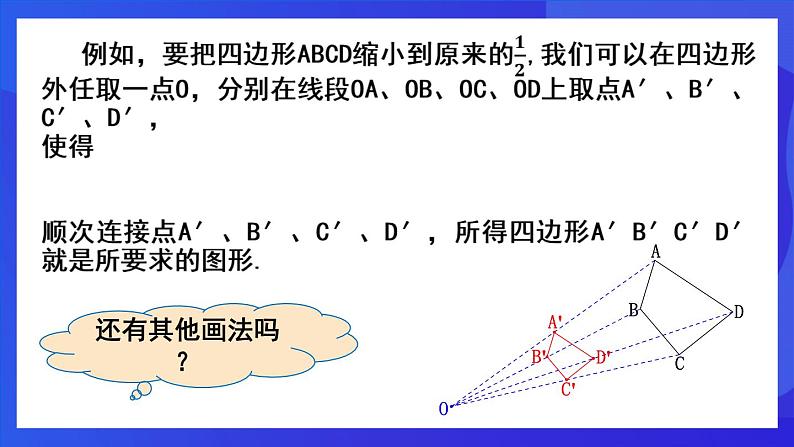
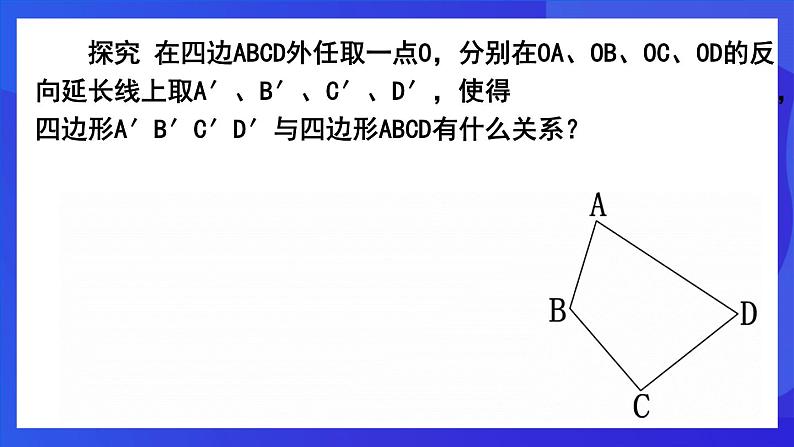
探究 在四边ABCD外任取一点O,分别在OA、OB、OC、OD的反向延长线上取A′、B′、C′、D′,使得 ,四边形A′B′C′D′与四边形ABCD有什么关系?
A'(___,___),B'(___,___);A″(___,___),B″(___,___).
探究 如图,△AOC三个顶点的坐标分别为A(4,4),O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.观察对应顶点坐标的变化,你有什么发现?
A'(___,___),O(___,___),C'(___,___);A″(___,___),O(___,___),C″(____,___).
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y )对应的位似图形上的点的坐标为(kx, ky )或(-kx ,-ky ).
分析:由于要画的图形是三角形,所以关键是确定它的各顶点坐标.根据前面总结的规律,点A的对应点A′的坐标为 即(-3,6).类似地,可以确定其他顶点的坐标.
解:如图,利用位似中对应点的坐标的变化规律,分别取点A′(-3,6),B ′(-3, 0), O (0, 0).顺次连接点A′,B ′,O,所得△ A′B ′O就是要画的一个图形.
解:如图,利用位似中对应点的坐标的变化规律,分别取点A''(3,-6),B'' (3,0),O(0,0).顺次连接A'',B'',O,所得△A''B''O就是要画的一个图形.
1.如图,△ABC 与△DEF 是位似图形,点O 是位似中心,相似比是1:2,已知DE=4,则AB 的长是( ) A.2 B.4 C.8 D.1
2.在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),B (3,6),C(-3,3). 以原点O为位似中心,画出四边形OABC的位似图形,使它与四边形OABC的相似是2:3.
解:依题意得A' (-3,3),B' (-4,1),C' (-2,0),D'(-1,2);或A" (3,-3),B"(4,-1),C"(2,0),D"(1,-2).
1.图中的两个三角形是位似图形,它们的位似中心是( ) A.点PB.点O C.点MD.点N
2.如图,在6×8网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均为小正方形的顶点.(1)以O 为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC 位似,且位似比为 1∶2;(2) 连接(1)中的AA′,求四边形AA′C ′C 的周长.(结果保留根号)
分析:(1)根据位似比是1∶2,画出以O 为位似中心的△A′B ′C ′;(2)根据勾股定理求出AC,A′C′的长,由于AA′,CC′的长易得,相加即可求得四边形AA′C′C的周长.解:(1)如图所示: (2)AA′=CC′=2. 在Rt△OA′C ′中, OA′=OC′=2,得A′C′= 同理可得AC= ∴四边形AA′C′C的周长=
1.位似的概念及画法位似图形的概念位似图形的性质画位似图形2.(1)当位似图形在原点同侧时,其对应顶点的坐标的比为k (k>0);当位似图形在原点两侧时,其对应顶点的坐标的比为-k. (2)当k>1时,图形扩大;当0<k<1时,图形缩小.
1.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点到位似中心的距离之比等于相比.其中正确的序号是( ) A.② B.①② C.③④ D.②③④
6,如图,在平面直角坐标系中,将△ABC 进行位似变换得到△A1B1C1.(1)求△A1B1C1与△ABC 的相似比;(2)画出△A1B1C1关于y 轴对称的△A2B2C2;(3)设点P (a,b)为△ABC 内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是多少?
解:(1)△A1B1C1与△ABC的相似比是2:1. (2)如图所示. (3)∵点P (a,b)为△ABC 内一点, ∴依上述两次变换后,点P 在△A2B2C2内的对应点P2的坐标是(-2a,2b).
相关课件
这是一份初中数学人教版(2024)九年级下册27.3 位似教学演示ppt课件,共1页。
这是一份人教版(2024)九年级下册27.3 位似教学演示ppt课件,共33页。PPT课件主要包含了教学目标,作图步骤,例题练习等内容,欢迎下载使用。
这是一份初中数学鲁教版 (五四制)八年级下册9 利用位似放缩图形试讲课课件ppt,共38页。PPT课件主要包含了逐点学练,本节小结,作业提升,本节要点,学习流程,知识点,位似多边形的定义,位似多边形的性质,位似图形的画法,利用位似放缩图形等内容,欢迎下载使用。










