初中数学人教版（2024）八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形精练

这是一份初中数学人教版（2024）八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形精练，文件包含人教版数学八年级下册精讲精练185正方形的性质与判定原卷版doc、人教版数学八年级下册精讲精练185正方形的性质与判定解析版doc等2份试卷配套教学资源，其中试卷共83页， 欢迎下载使用。

知识点一
正方形的定义
●●定义：四条边都相等，四个角都是直角的四边形叫做正方形.
◆1、正方形的四条边都相等，说明正方形是特殊的菱形；
◆2、正方形的四个角都是直角，说明正方形是特殊的矩形.即：正方形是特殊的矩形又是特殊的菱形.
知识点二
正方形的性质
◆1、具有矩形、菱形、平行四边形的一切性质，即
①边：四条边相等，邻边垂直，对边平行；
②角：四个角都是直角；
③对角线：对角线相等，互相垂直平分，每条对角线平分一组对角；
④正方形式轴对称图形，有四条对称轴；
◆2、正方形的面积计算
①边长的平方；②对角线平方的一半；
◆3、正方形特有的性质：
①正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的两条对角线把正方形分成四个全等的等腰直角三角形；
②周长相等四边形中，正方形的面积最大.
知识点三
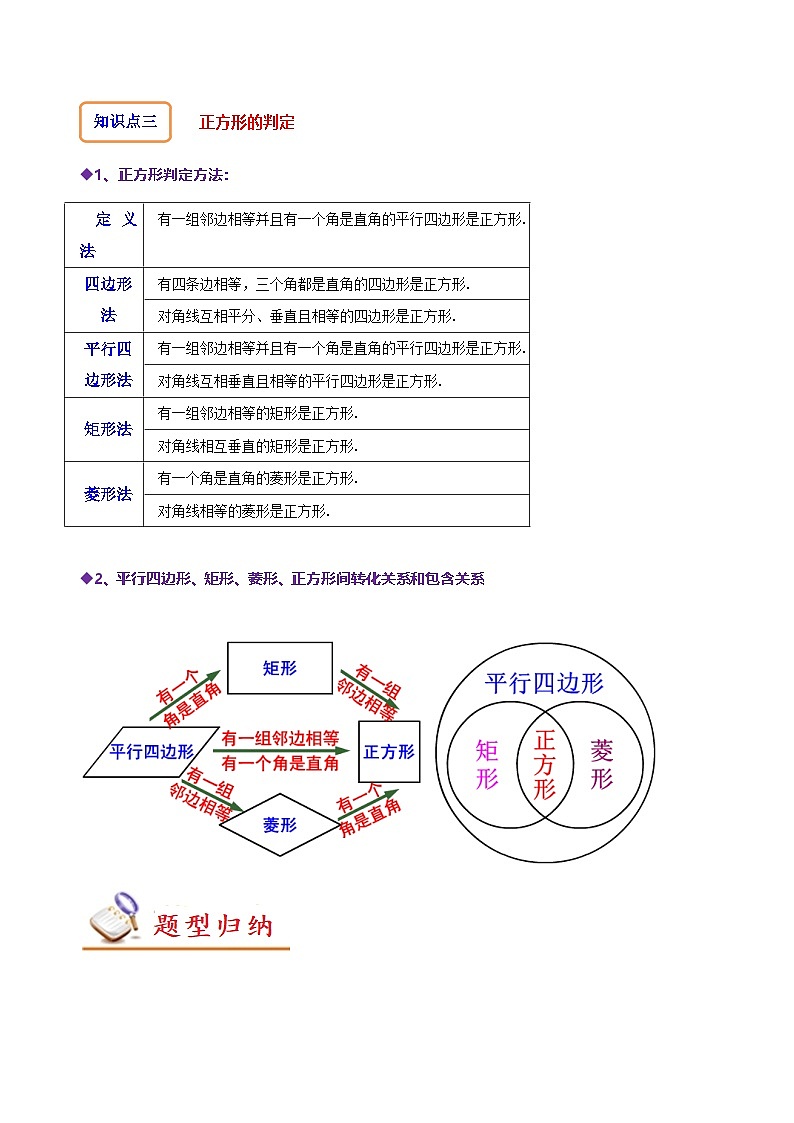
正方形的判定
◆1、正方形判定方法：
◆2、平行四边形、矩形、菱形、正方形间转化关系和包含关系
题型一 利用正方形的性质求角度
【例题1】（2022秋•竞秀区期中）如图，在正方形ABCD外侧，作等边三角形ADE，AC、BE相交于点F，则∠BEA为（ ）
A．15°B．30°C．45°D．55°
【变式1-1】（2022秋•文山市期末）如图，四边形ABCD是正方形，延长AB到点E，使AE＝AC，则∠BCE的度数是（ ）
A．62.5°B．45°C．32.5°D．22.5°
【变式1-2】（2022秋•新城区期末）如图，在正方形ABCD中，E为对角线BD上一点，连接AE、CE，∠BCE＝70°，则∠EAD为（ ）
A．10°B．15°C．20°D．30°
【变式1-3】（2022秋•保定期末）如图，在正方形ABCD中，等边△AEF的顶点E，F分别在边BC和CD上，则∠AEB等于（ ）
A．60°B．70°C．75°D．80°
【变式1-4】（2022秋•太原期中）如图，点E．F分别是正方形ABCD内部、外部一点，四边形ADFE与四边形BCFE均为菱形，则∠CBE的度数等于 ．
【变式1-5】（2022秋•沙坪坝区期末）如图，在正方形ABCD中，点E，点F分别是对角线BD，AC上的点，连接CE，EF，DF，若EF∥BC，且∠CEF＝15°，则∠EDF的度数为（ ）
A．22.5°B．25°C．30°D．35°
【变式1-6】（2023•渝中区校级开学）如图，E、F、H分别为正方形ABCD的边AB、BC、CD上的点，连接DF，HE，且HE＝DF，DG平分∠ADF交AB于点G．若∠BEH＝52°，则∠AGD的度数为（ ）
A．26°B．38°C．52°D．64°
题型二 利用正方形的性质求线段长
【例题2】（2022春•如皋市校级月考）如图，正方形ABCD的边长为2，点E在对角线BD上，且∠BAE＝22.5°，则BE的长为（ ）
A．1B．C．22D．1

【变式2-1】（2022秋•朝阳区校级期末）如图，直线l过正方形ABCD的顶点A，BE⊥l于点E，DF⊥l于点F．若BE＝2，DF＝4，则的EF长为 ．
【变式2-2】（2022秋•九龙坡区期末）如图，在正方形ABCD中，O为对角线AC、BD的交点，E、F分别为边BC、CD上一点，且OE⊥OF，连接EF．若∠AOE＝150°，DF，则EF的长为（ ）
A．B．C．D．31
【变式2-3】（2022秋•青田县期末）如图，正方形ABCD的边长为10，AG＝CH＝8，BG＝DH＝6，连结GH，则线段GH的长为（ ）
A．B．C．D．
【变式2-4】（2022秋•朝阳区校级期末）如图，正方形ABCD的边长为7，点E是AB上的一点，且AE＝3，将正方形沿DE翻折，点A落在点G处，延长EG交BC于点F，则CF的长是 ．
【变式2-5】（2022秋•沙坪坝区校级期中）如图，边长为5的正方形ABCD中，点E、F分别在边BC、CD上，连接AE、AF、EF．已知AF平分∠DFE，BE＝2，则DF的长为（ ）
A．2B．4C．D．
题型三 利用正方形的性质求周长或面积
【例题3】（2022秋•汉台区期末）如图，正方形ABCD的边长为8，在各边上顺次截取AE＝BF＝CG＝DH＝6，则四边形EFGH的面积是（ ）
A．34B．36C．40D．100
【变式3-1】（2022秋•永安市期中）正方形的周长为8cm，则它的面积为（ ）
A．2cm2B．4cm2C．6cm2D．8cm2
【变式3-2】（2022•礼县校级模拟）如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为（ ）
A．3B．4C．5D．6
【变式3-3】（2022春•南岗区校级月考）正方形一条对角线长为2，则周长为（ ）
A．4B．4C．8D．8
【变式3-4】（2022秋•路北区校级期末）如图，小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起，其中直角三角板的直角顶点落在点A处，两条直角边分别与CD交于点F，与CB延长线交于点E，则四边形AECF的面积是 ．
【变式3-5】（2022•珠海校级三模）如图，E是正方形ABCD内一点，AE⊥DE于E，AE＝2cm，则△ABE的面积是（ ）
A．5B．4C．3D．2
题型四 利用正方形的性质进行证明
【例题4】（2022秋•茂南区期末）如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连接CE、DF．求证：CE＝DF．
【变式4-1】（2022秋•永丰县校级期末）如图，在正方形ABCD中，点P在边AD上，且不与点A，D重合，点H在边AB上，且不与点A，B重合，连接BP、CH，BP与CH交于点E．若BP＝CH，求证：BP⊥CH．
【变式4-2】（2022秋•双牌县期末）如图，四边形ABCD，BEFG均为正方形，连接CE，AG．
求证：CE＝AG．
【变式4-3】（2022秋•安丘市校级期末）如图，正方形ABCD的对角线AC、BD相交于点O，G是CD边上一点，连接BG交AC于E，过点A作AM⊥BG，垂足M，AM交BD于点F．
（1）求证：OE＝OF．
（2）若H是BG的中点，BG平分∠DBC，求证：DG＝2OE．
【变式4-4】（2022春•顺义区校级月考）如图，在正方形ABCD中，Q为对角线BD上一点（DQ＞BQ），连接AQ、CQ．
（1）求证：AQ＝CQ；
（2）过点Q作QR⊥BD交BC于点R，延长CB至点H使BH＝CR，连接AH．
①依题意补全图形；
②用等式表示AH与CQ之间的数量关系，并证明．
【变式4-5】（2022•珠海校级三模）如图，E是正方形ABCD的BC边上一点（E不与B、C重合），EG⊥AC于G，F在BC的延长线上，且CF＝BE，连接AE、DF和DG．
（1）若连接GF，求证：DG＝GF；
（2）若∠BAE＝30°，求∠AGD的度数．
题型五 正方形判定的条件
【例题5】（2022秋•武侯区期末）下列说法不正确的是（ ）
A．对角线互相垂直平分的四边形是正方形
B．菱形的对角线互相垂直
C．矩形的对角线相等
D．对角线互相平分的四边形是平行四边形
【变式5-1】（2022秋•漳州期末）如图，在矩形ABCD中，对角线AC、BD交于点O，添加下列一个条件，能使矩形ABCD成为正方形的是（ ）
A．BD＝ACB．DC＝ADC．∠AOB＝60°D．OD＝CD
【变式5-2】（2022春•庄浪县期中）如图，下列三组条件中，能判定平行四边形ABCD是正方形的
有（ ）
①AB＝BC，∠BAD＝90°；②AC⊥BD，AC＝BD；③OA＝OD，BC＝CD．
A．0个B．1个C．2个D．3个
【变式5-3】（2022秋•金水区校级期中）已知四边形ABCD是平行四边形，下列结论中错误的有（ ）
①当AB＝DC时，它是菱形；
②当AC⊥BD时，它是菱形；
③当∠ABC＝90°时，它是矩形；
④当AC＝BD时，它是正方形．
A．1个B．2个C．3个D．4个
【变式5-4】（2022秋•东明县校级期末）如图，在△ABC中，点D，E，F分别在边BC，AB，CA上，且DE∥CA，DF∥BA．下列四种说法：
①四边形AEDF是平行四边形；
②如果∠BAC＝90°，那么四边形AEDF是矩形；
③如果AD平分∠BAC，那么四边形AEDF是菱形；
④如果AD⊥BC，且AB＝AC，那么四边形AEDF是正方形．
其中，正确的有（ ）
A．1个B．2个C．3个D．4个
【变式5-5】（2022•黑龙江一模）平行四边形ABCD的对角线AC与BD相交于点O，且AC⊥BD，请添加一个条件： ，使得平行四边形ABCD为正方形．
【变式5-6】（2022秋•郏县期中）如图，E、F、G、H分别是AB、BC、CD、DA的中点．要使四边形EFGH是正方形，BD、AC应满足的条件是 ．
题型六 正方形的判定的证明
【例题6】（2022•邵阳）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F在对角线BD上，且BE＝DF，OE＝OA．
求证：四边形AECF是正方形．
【变式6-1】（2022春•宽城区期末）如图，在矩形ABCD中，点E、F分别在边AB、BC上，DE＝AF，DE⊥AF于点G．
（1）求证：△ABF≌△DAE．
（2）求证：四边形ABCD是正方形．
【变式6-2】（2021秋•泾阳县期末）如图，已知四边形ABCD是矩形，点E在对角线AC上，点F在边CD上（点F与点C、D不重合），BE⊥EF，且∠ABE+∠CEF＝45°．求证：四边形ABCD是正方形．
【变式6-3】（2022秋•中宁县期中）已知：如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于点E，交AC于点F．
（1）试判定四边形AEDF的形状，并证明你的结论；
（2）△ABC满足什么条件时，四边形AEDF是正方形．
【变式6-4】（2022春•唐河县期末）如图所示△ABC中，∠C＝90°，∠CAB，∠ABC的平分线相交于D点，DE⊥BC于点E，DF⊥AC于点F．
（1）求证：四边形CEDF为正方形；
（2）若AC＝6，BC＝8，则CE的长为 ．
【变式6-5】（2022春•隆安县期末）如图，四边形ABCD是平行四边形，AE∥BD，AE与CB的延长线交于点E，DE交AB于F．
（1）求证：BC＝BE；
（2）连接CF，若∠ADF＝∠BCF且AD＝2AF，求证：四边形ABCD是正方形．
题型七 正方形的性质与判定的综合应用
【例题7】（2022春•河西区期末）如图，点E，F，P，Q分别是正方形ABCD的四条边上的点，并且AF＝BP＝CQ＝DE，则下列结论不一定正确的是（ ）
A．∠AFP＝∠BPQ
B．EF∥QP
C．四边形EFPQ是正方形
D．四边形PQEF的面积是四边形ABCD面积的一半
【变式7-1】（2022春•赣县区校级期末）如图，E、F、M、N分别是正方形ABCD四条边上的点，且
AE＝BF＝CM＝DN
（1）求证：四边形EFMN是正方形；
（2）若AB＝7，AE＝3，求四边形EFMN的周长．
【变式7-2】（2022秋•胶州市校级月考）如图所示，在正方形ABCD中，DF＝AP＝BQ＝CE．
（1）试判断四边形PQEF是否是正方形，并证明；
（2）PE是否总过某一定点，并说明理由．
【变式7-3】（2022秋•砀山县校级月考）如图，正方形ABCD中，AB＝3，点E是对角线AC上的一点，连接DE．过点E作EF⊥ED，交AB于点F，以DE，EF为邻边作矩形DEFG，连接AG．
（1）求证：矩形DEFG是正方形；
（2）求AG+AE的值；
（3）若F恰为AB的中点，求正方形DEFG的面积．
【变式7-4】（2022春•南谯区校级月考）如图1，四边形ABCD为正方形，E为对角线AC上一点，连接DE，BE．
（1）求证：BE＝DE；
（2）如图2，过点E作EF⊥DE，交边BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．
①求证：矩形DEFG是正方形；
②若正方形ABCD的边长为9，CG＝3，求正方形DEFG的边长．
【变式7-5】（2022春•杭州期中）已知：如图，在正方形ABCD中，E，F分别是BC，CD上的点，AE、BF相交于点P，并且AE＝BF．
（1）如图1，判断AE和BF的位置关系？并说明理由；
（2）若AB＝8，BE＝6，求BP的长度；
（3）如图2，FM⊥DN，DN⊥AE，点F在线段CD上运动时（点F不与C、D重合），四边形FMNP是否能否成为正方形？请说明理由．
题型八 正方形中的最短问题
【例题8】（2022•资阳）如图，正方形ABCD的对角线交于点O，点E是直线BC上一动点．若AB＝4，则AE+OE的最小值是（ ）
A．B．C．D．
【变式8-1】（2022•德州）如图，正方形ABCD的边长为6，点E在BC上，CE＝2．点M是对角线BD上的一个动点，则EM+CM的最小值是（ ）
A．B．C．D．
【变式8-2】（2022•苏州模拟）如图，正方形ABCD的边长为，点E，F分别是对角线AC的三等分点，点P是边AB上一动点，则PE+PF的最小值是（ ）
A．B．C．D．
【变式8-3】如图，正方形ABCD的边长为3，点E在BC上，且CE＝1，P是对角线AC上的一个动点，则PB+PE的最小值为 ．
【变式8-4】（2022秋•莲湖区校级月考）如图，在正方形ABCD中，AB＝3，点E在CD边上，且DE＝2CE，点P是对角线AC上的一动点．则PE+PD的最小值是（ ）
A．B．C．3D．3
【变式8-5】（2022•青岛一模）如图，正方形ABCD的边长为6，点E，F分别为边BC，CD上两点，CF＝BE，AE平分∠BAC，连接BF，分别交AE，AC于点G，M，点P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM，则PM+PN的最小值为 ．
定义法
有一组邻边相等并且有一个角是直角的平行四边形是正方形.
四边形法
有四条边相等，三个角都是直角的四边形是正方形.
对角线互相平分、垂直且相等的四边形是正方形.
平行四边形法
有一组邻边相等并且有一个角是直角的平行四边形是正方形.
对角线互相垂直且相等的平行四边形是正方形.
矩形法
有一组邻边相等的矩形是正方形.
对角线相互垂直的矩形是正方形.
菱形法
有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
解题技巧提炼
正方形中求角度的问题要善于抓住正方形中的特殊角度90°、45°以及四边相等的性质.
解题技巧提炼
由于正方形的对角线相等且互相垂直平分，所以对于正方形的对角线及边这两个元素中知道其中一个的长度，都能根据勾股定理求出另一个.在计算中要利用等腰直角三角形的相关知识.
解题技巧提炼
正方形的周长：边长×4.
正方形的面积：（1）边长的平方；（2）对角线乘积的一半；
解题技巧提炼
通过证明三角形全等得到边和角相等，再进一步得到平行或垂直，是有关正方形中证明边或角相等的最常用的方法，而正方形的四条 边相等，四个角都是直角为证明三角形全等提供了条件.
解题技巧提炼
正方形的判定方法：
①先判定四边形是矩形，再判定这个矩形有一组邻边相等；
②先判定四边形是菱形，再判定这个菱形有一个角为直角．
③还可以先判定四边形是平行四边形，再用①或②进行判定．
解题技巧提炼
判定一个四边形是正方形时，往往先判定它是矩形（或菱形），再补充一个想对应的一个或两个其它有关边、角、对角线的条件，即可证明.
解题技巧提炼
正方形的判定可以确定正方形的存在，再利用正方的性质，可以得出线段或角的对应关系从而解决问题.
解题技巧提炼
在解决正方形中的最短问题时，利用轴对称、平移等变换把已知问题转化为容易解决的问题，从而作出最短线段和.