华东师大版（2024）8.2 多边形的内角和与外角和背景图ppt课件

这是一份华东师大版（2024）8.2 多边形的内角和与外角和背景图ppt课件，共25页。PPT课件主要包含了多边形的内角和，内角和计算公式，多边形的定义，n×180°，n-2×180°，n边形外角和，360°，还有其他解法吗，多边形的外角和等内容，欢迎下载使用。
8.2 多边形的内角和与外角和
8.2.2 多边形的外角和
(n-2) × 180 °(n ≥ 3 的整数)
由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形，也即我们通常所说的多边形
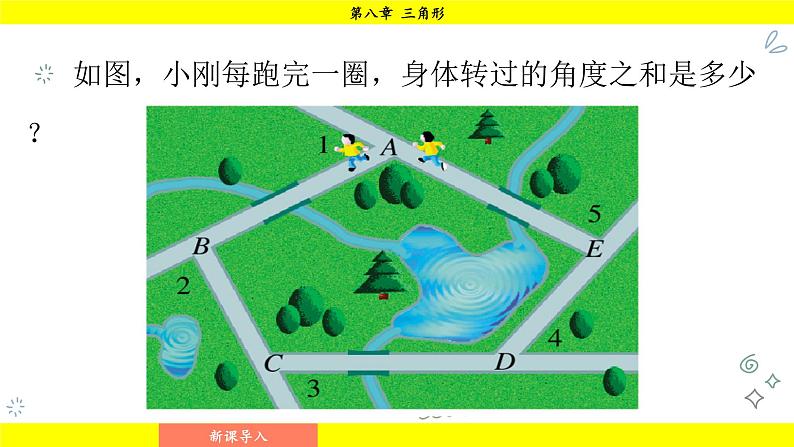
如图，小刚每跑完一圈，身体转过的角度之和是多少？
与多边形的每个内角相邻的外角分别有两个，这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加，得到的和称为多边形的外角和.
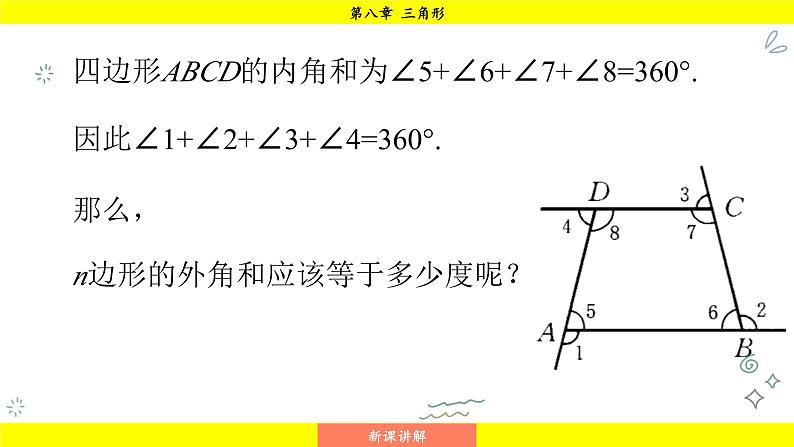
如图，∠1+∠2+∠3+∠4就是四边形ABCD的外角和. 从图中可以知道：（∠1+∠5）+（∠2+∠6）+（∠3+∠7）+（∠4+∠8） =4×180°，所以 ∠1+∠2+∠3+∠4 = 4 × 180°－（∠5+∠6+∠7+∠8）.
四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.因此∠1+∠2+∠3+∠4=360°.那么，n边形的外角和应该等于多少度呢？
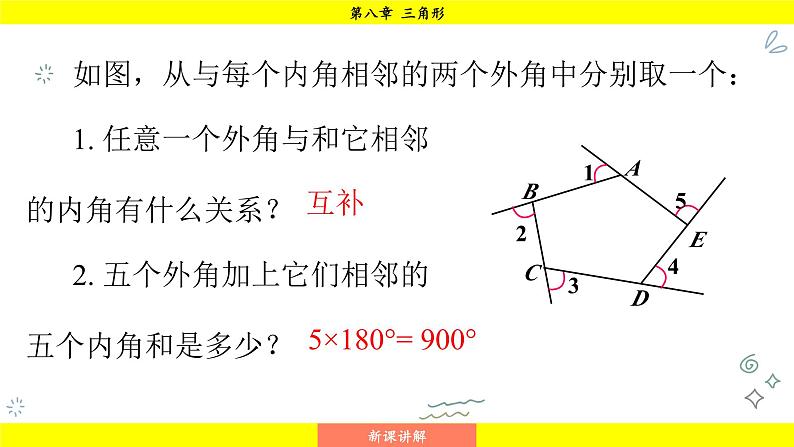
如图，从与每个内角相邻的两个外角中分别取一个：1. 任意一个外角与和它相邻的内角有什么关系？2. 五个外角加上它们相邻的五个内角和是多少？
5×180°= 900°
如图，从与每个内角相邻的两个外角中分别取一个：3. 这五个平角和与五边形的内角和、外角和有什么关系？
五个平角和(900°)－五边形的内角和(540°)=五边形的外角和(360°)
根据n边形的每一个内角与和它相邻的外角都互为补角,可以求得n边形的外角和.据此,请将数据填入表中.
4×180°= 720°
6×180°= 1080°
7×180°= 1260°
因此，任意多边形的外角和都为360°.
与 n 边形的每个内角相邻的外角分别有两个， 这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加，得到的和称为 n 边形的外角和.
－(n－2) × 180°
= n 个平角和－n 边形内角和
即，n边形的外角和等于360度.
例3 一个多边形的每个外角都是72°，这个多边形是几边形？解： 设这个多边形的边数为 n，根据题意，得 n·72°=360°.解得 n = 5. 因此，这个多边形是五边形.
例4 一个多边形的内角和等于它外角和的 5 倍，这个多边形是几边形？ 解： 设这个多边形的边数为 n，根据题意，得 (n－2)·180°= 5× 360°. 解得 n = 12. 因此，这个多边形是十二变形.
已知一个多边形的每个内角与和它相邻的一个外角的比都是 7∶2，求这个多边形的边数.解法一：设这个多边形的内角为 7x°，外角为 2x°，根据题意得7x + 2x = 180，
解得 x = 20.即内角是 140°，外角是 40°.360°÷40° = 9.答：这个多边形的边数为 9.
解法二：设这个多边形的边数为 n ，根据题意得解得 n = 9.答：这个多边形的边数为 9.
1.一个多边形的每一个外角都等于45°，这个多边形是几边形？它的每一个内角是多少度？
2.在一个多边形中， 它的内角最多可以有几个是锐角？
1. 判断对错：(1) 当多边形边数增加时，它的外角和也随着增加. ( )(2) 三角形的外角和与八边形的外角和相等．( )
2. 一个多边形的所有内角与一个外角的和是 2380°，则这个多边形的边数为______.
解：设这个多边形的边数为 x ( x 为正整数)，则这个多边形的内角和为 ( x-2)×180°，由题意可得，2380 -180 < (x-2)×180 < 2380，解得 14.22 < x < 15.22因为 x 为正整数，所以 x =15，即这个多边形的边数为15.
3. 如图，求图中 x 的值. 解：由题意可得， 3x+90+90 = 360. 解得 x = 60.
任意多边形的外角和都为360°特别注意：与边数无关
从与每个内角相邻的两个外角中分别取一个相加，得到的和称为多边形的外角和.