天津市红桥区2024-2025学年上学期八年级期末 数学试卷（含解析）

这是一份天津市红桥区2024-2025学年上学期八年级期末 数学试卷（含解析），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．在一些美术字中，有的汉字是轴对称图形，下列四个汉字中，可以看作轴对称图形的是（ ）
A．B．C．D．
2．一种病毒的直径约为，将数据用科学记数法表示应为（ ）
A．B．
C．D．
3．以下列长度的各组线段为边，能组成三角形的是（ ）
A．B．
C．D．
4．下列计算正确的是（ ）
A．B．
C．D．
5．已知 AF 是等腰 △ABC 底边 BC 上的高，若点 F 到直线 AB 的距离为3，则点 F 到直线 AC 的距离为（ ）
6．计算的结果是（ ）
A．B．C．1D．
7．将一个含角的三角尺和直尺如图放置，若，则的度数是（ ）
A．30°B．C．D．60°
8．下列计算正确的是
A．B．
C．D．
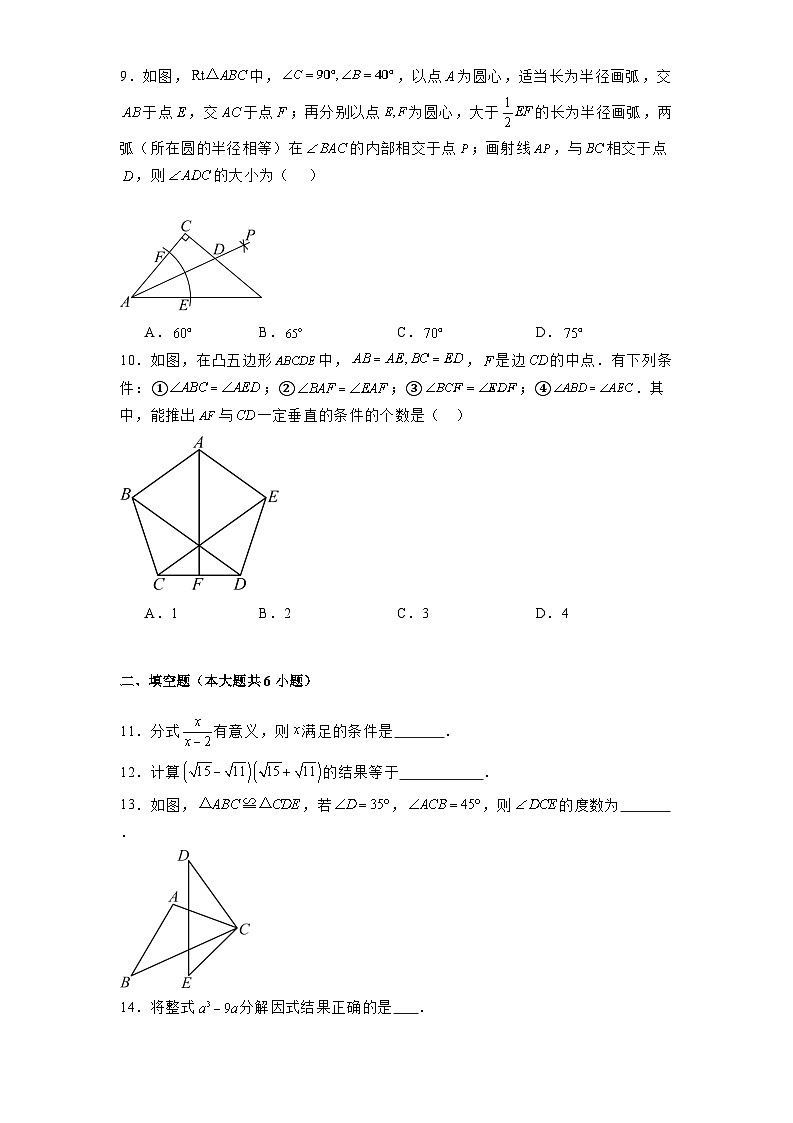
9．如图，中，，以点为圆心，适当长为半径画弧，交于点，交于点；再分别以点为圆心，大于的长为半径画弧，两弧（所在圆的半径相等）在的内部相交于点；画射线，与相交于点，则的大小为（ ）

A．B．C．D．
10．如图，在凸五边形中，，是边的中点．有下列条件：①；②；③；④．其中，能推出与一定垂直的条件的个数是（ ）
A．1B．2C．3D．4
二、填空题（本大题共6小题）
11．分式有意义，则满足的条件是 ．
12．计算的结果等于 ．
13．如图，，若，，则的度数为 ．
14．将整式分解因式结果正确的是 ．
15．分式方程的解为 ．
16．如图，在中，，，．
（1）的面积等于 ．
（2）是边上的定点，是边上的动点（），且，连接．当取得最小值时，请在如图所示的矩形区域内，用无刻度的直尺和圆规，画出点，并简要说明点的位置是如何找到的（保留作图痕迹，不要求证明） ．
三、解答题（本大题共7小题）
17．在平面直角坐标系中，的顶点A，B，C的坐标分别为−3,2，，．若与关于y轴对称，点A，B，C的对应点分别为，，．请在图中作出，并写出点，，的坐标．
18．计算：
(1)；
(2)．
19．如图，在中，，，是边上的高，是的平分线．
(1)求的大小；
(2)求的大小．
20．先化简，再求值：
(1)，其中；
(2)，其中．
21．如图，在中，D为边的中点，过点B作交的延长线于点E．
(1)求证：；
(2)若，求证：．
22．某校组织师生去距离学校的纪念馆开展研学活动．骑行爱好者张老师骑自行车先行后，其余师生乘汽车出发，结果同时到达．已知汽车的速度是张老师骑自行车的速度的3倍．设张老师骑自行车的速度为．
请根据相关信息，回答下列问题：
(1)用含有的代数式填空：
①汽车的速度为________；
②张老师骑自行车从学校到纪念馆所用的时间为_________；
③其余师生乘汽车从学校到纪念馆所用的时间为_________；
(2)求张老师骑自行车的速度．
23．已知是边长为6的等边三角形，是边上的动点（点不与点，重合），以为边作等边三角形（点在的上方）．
(1)如图①，当D为边的中点时，求证：；
(2)如图②，连接，求证：；
(3)F为边的中点，连接，当取得最小值时，延长与直线相交于点G，求线段的长（直接写出结果即可）．
参考答案
1．【答案】A
【分析】利用轴对称图形定义进行解答即可．
【详解】解：A、“业”可以看作轴对称图形，故此选项符合题意；
B、“精”不可以看作轴对称图形，故此选项不合题意；
C、“于”不可以看作轴对称图形，故此选项不合题意；
D、“勤”不可以看作轴对称图形，故此选项不合题意；
故此题答案为A．
2．【答案】C
【分析】科学记数法的表示形式为，确定n值的方法，当原数的绝对值时，把原数变为a时，小数点向左移动的位数即为n的值；当原数的绝对值时，把原数变为a时，小数点向右移动位数的相反数即为n的值，由此即可求解．
【详解】解：，
故此题答案为C ．
3．【答案】B
【分析】根据三角形三边数量关系“两边之和大于第三边，两边之差小于第三边”判定即可．
【详解】解：A、，不能构成三角形，不符合题意；
B、，能构成三角形，符合题意；
C、，不能构成三角形，不符合题意；
D、，不能构成三角形，不符合题意；
故此题答案为B ．
4．【答案】D
【分析】根据同底数幂的乘除法则与积的乘方法则计算，即可求解．
【详解】解：A. ，故该选项不正确，不符合题意；
B. ，故该选项不正确，不符合题意；
C. ，故该选项不正确，不符合题意；
D. ，故该选项正确，符合题意；
故此题答案为D．
5．【答案】C
【详解】解： 如图，
∵ AF 是等腰 △ABC 底边 BC 上的高，
∴ AF 平分 ∠BAC，
∴点 F 到直线 AB， AC 的距离相等，
∵点 F 到直线 AB 的距离为3，
∴点 F 到直线 AC 的距离为3．
故此题答案为C．
6．【答案】C
【分析】根据同分母分式的加减法法则计算即可求解．
【详解】解：，
故此题答案为C．
7．【答案】B
【分析】根据对顶角相等和三角形的内角和定理，即可求解．
【详解】解：如图所示，
由题意得，，，
∴，
故此题答案为B．
8．【答案】D
【分析】根据整式的乘法运算法则计算即可求解．
【详解】解：A、，故原选项错误，不符合题意；
B、，故原选项错误，不符合题意；
C、，故原选项错误，不符合题意；
D、，正确，符合题意；
故此题答案为D ．
9．【答案】B
【详解】解：∵，
∴，
由作图知，平分，
∴，
又
∴
故此题答案为B.
10．【答案】C
【分析】如图所示，连接，证明，，可得条件①可推出结论；证明，，可得条件②可推出结论；证明，，可得条件③可推出结论；④不能找出三角形全等，及相关的数量关系，故不能推出结论，由此即可求解．
【详解】解：如图所示，连接，
①，
∵，
∴，
∴，
∵是边的中点，
∴，
在和中，
，
∴，
∴，
∵，
∴，即能推出与一定垂直；
②，
在和中，
∵，
∴，
∴，
在和中，
，
∴，
∴，
∴，即，
∵，
∴，即能推出与一定垂直；
③，
在和中，
，
∴，
∴，
在和中，
∵，
∴，
∴，
∴，即，
∵，
∴，即能推出与一定垂直；
④,
不能证明三角形全等，找不出数量关系，故不能推出与一定垂直；
综上所述，能推出与一定垂直的有①②③，共3个，
故此题答案为C ．
11．【答案】
【分析】当分母不为0时，分式有意义．根据分式有意义的条件得到，即可求解．
【详解】解：∵分式有意义，
∴，
∴
12．【答案】4
【分析】根据二次根式乘法运算，利用平方差公式计算即可．
【详解】解：
13．【答案】/100度
【分析】先利用全等三角形的性质，求出，再利用三角形内角和求出的度数即可．
【详解】解：由，，
∴，
∵，
∴
14．【答案】
【详解】解：原式
15．【答案】
【分析】去分母，化分式方程为整式方程，解方程并检验，即可求解．
【详解】解：，
方程两边同时乘以得，，
解得：，
当时，，
∴是原方程的解
16．【答案】 6 见解析
【分析】（1）根据三角形面积的计算公式计算即可；
（2）作点关于的对称点，再过点作垂足为点，在上截取，连接交于点，再在上截取，由，结合两点之间线段最短即可得到点的位置．
【详解】解：（1）∵，，，
∴；
（2）作点关于的对称点，再过点作垂足为点，在上截取，连接交于点，再在上截取，点的位置如图所示．
17．【答案】图见解析，，，
【详解】解：如图，即为所求．
由图可得，，，．
18．【答案】(1)
(2)
【分析】（1）根据整式的除法运算法则计算，系数除以系数，同底数幂相除，底数不变，指数相减，由此即可求解；
（2）运用完全平方公式展开，多项式乘以多项式的运算展开，最后再运用整式加减运算即可求解．
【详解】（1）解：
；
（2）解：
．
19．【答案】(1)
(2)
【分析】（1）求出，则，，即可解决问题；
（2）由角平分线的定义得，再由三角形内角和定理即可得出结论．
【详解】（1）解：是边上的高，
，
，，
，，
；
（2）解：是的平分线，
，
．
20．【答案】(1)；
(2)；
【分析】（1）根据同分母的分式减法进行计算，最后代入求值，即可．
（2）先通分，再算分式减法和除法，进行化简，最后代入求值，即可．
【详解】（1）解：
当时，原式；
（2）解：
；
当时，原式
21．【答案】(1)证明见解析
(2)证明见解析
【分析】（1）由线段中点的定义可得，由两直线平行内错角相等可得，，然后利用即可得出结论；
（2）由（1）可得，于是可得，由已知条件可得，然后利用可证得，于是结论得证．
【详解】（1）证明：∵D为边的中点，
∴，
∵，
，，
；
（2）证明：由（1）可得：，
，
又，
，
又，
，
．
22．【答案】(1)①3x；②；③
(2)张老师骑自行车的速度为
【分析】（1）①根据汽车速度是张老师速度的3倍列式即可；②根据行程中时间等于路程除以速度列式即可；③根据时间等于路程除以速度列式即可；
（2）根据数量关系，列分式方程求解即可．
【详解】（1）解：①设张老师骑自行车的速度为，
∴汽车的速度为
②去距离学校的纪念馆开展研学活动，设张老师骑自行车的速度为，
∴张老师骑自行车从学校到纪念馆所用的时间为，
故答案为：；
③去距离学校的纪念馆开展研学活动，汽车的速度为，
∴其余师生乘汽车从学校到纪念馆所用的时间为
（2）解：根据题意列式得，，
解得，，，
检验，当x=0时，原分式方程分母为0，不符合题意，舍去，
当时，原分式方程有意义，符合题意，
∴张老师骑自行车的速度为．
23．【答案】(1)见解析
(2)见解析
(3)3
【分析】（1）根据等边三角形的性质和三线合一的性质即可得结论；
（2）根据“”证明，得，再根据内错角相等，两直线平行可得结论；
（3）根据可知：点在过点与平行的射线上运动，如图③，作点关于直线的对称点，连接交直线于，连接，此时的值最小，根据全等三角形的性质和判定即可解答．
【详解】（1）证明：是等边三角形，为边的中点，
，
，
是等边三角形，
，，
，
，
；
（2）证明：和是等边三角形，
，，，
，
，
，
，
；
（3）解：为边的中点，，
，
由（2）知：，
点在过点与平行的射线上运动，
，
，
如图③，作点关于直线的对称点，连接交直线于，连接，
垂直平分，
，，
，，
，，
，
．
即线段的长为3．
A． 32
B．2
C．3
D． 72