人教A版（2019）高中数学必修第二册-小结（4）综合问题_课后练习

这是一份人教A版（2019）高中数学必修第二册-小结（4）综合问题_课后练习，共2页。
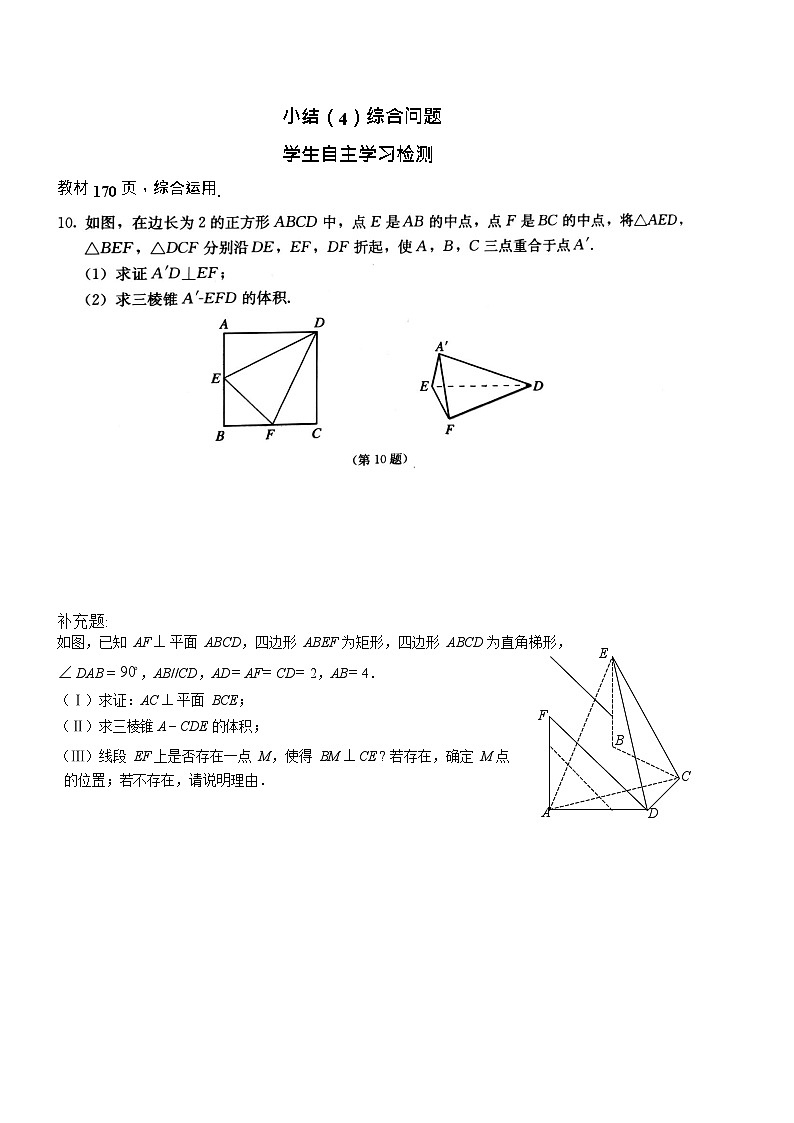
教材 170 页，综合运用.
补充题:
E
B
如图，已知 AF  平面 ABCD，四边形 ABEF 为矩形，四边形 ABCD 为直角梯形，
 DAB  90 ，AB//CD，AD= AF= CD= 2，AB= 4．
（Ⅰ）求证：AC  平面 BCE；
（Ⅱ）求三棱锥 A  CDE 的体积；F
（Ⅲ）线段 EF 上是否存在一点 M，使得 BM  CE ? 若存在，确定 M 点
的位置；若不存在，请说明理由．C
AD
答案与提示
教材 170 页，综合运用.
10．（1）折叠前，AD⊥AE，CD⊥CF，折叠后，A′D⊥A′E，A′D⊥A′F，又 A′E∩A′F=A′，所以 A′D⊥平面 A′EF，因此A′D⊥EF.
（2）V  1 . 提示：V
3
 1  A' D  A' E  A' F ．
6
补充题:
E
M
B
N C
证明: （Ⅰ）过 C 作 CN  AB，垂足为 N，
因为 AD  DC，所以四边形 ADCN 为矩形．所以 AN  DC  2.
2
F
2
又因为 AD  2，AB  4，所以 AC  2
所以 AC2+BC2  AB2，所以 AC  BC；
，CN  2 ，BC  2,
因为 AF  平面 ABCD，AF//BE，所以 BE  平面 ABCD，AD
所以 BE  AC，
又因为 BE  平面 BCE，BC  平面 BCE，BE BC  B， 所以 AC  平面 BCE．
(Ⅱ) 因为 AF  平面 ABCD，AF//BE，
所以 BE  平面 ABCD.
VACDE  VE ACD
 1 EB  S
3
ACD
 4 .
3
（Ⅲ）存在，点 M 为线段 EF 中点，证明如下：
在矩形 ABEF 中，因为点 M，N 为线段 FE，AB 的中点，所以四边形 BEMN 为正方形， 所以 BM  EN；
因为 AF  平面 ABCD，AD  平面 ABCD，所以 AF  AD.
在直角梯形 ABCD 中，AD  AB，又 AF AB  A，所以 AD  平面 ABEF， 又 CN//AD，所以 CN  平面 ABEF，
又 BM  平面 ABEF，所以 CN  BM；
又 CN EN  N，所以 BM  平面 ENC，又 EC  平面 ENC， 所以 BM  CE.