八年级数学开学摸底考（广州专用，人教版）-2024-2025学年初中下学期开学摸底考试卷

这是一份八年级数学开学摸底考（广州专用，人教版）-2024-2025学年初中下学期开学摸底考试卷，文件包含开学摸底考2024-2025学年春季期八年级数学开学摸底考人教版全解全析docx、开学摸底考2024-2025学年春季期八年级数学开学摸底考人教版考试版docx、开学摸底考2024-2025学年春季期八年级数学开学摸底考人教版参考答案docx、开学摸底考2024-2025学年春季期八年级数学开学摸底考人教版答题卡A3版docx等4份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
数学
（考试时间：120 分钟 试卷满分：120 分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用
橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答卡上。写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
第一部分 选择题(共 30 分)
一、选择题（本大题共 10 小题，每小题 3 分，满分 30 分．在每个小题给出的四个选项中，只有一项符合
题目要求的）
1．二十四节气，是历法中表示自然节律变化以及确立“十二月建”的特定节令，蕴含着悠久的文化内涵和
历史积淀，请你用数学的眼光观察下列四副代表“立春”、“立夏”、“芒种”、“白露”的作品，其中是轴
对称图形的是（
）
A．
B．
C．
D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，
这条直线叫做对称轴进行分析即可．
【解答】解：A，C，D 选项中的图形不能找到这样的一条直线，使图形沿这条直线折叠，直线两旁的部
分能够互相重合，所以不是轴对称图形，
B 选项中的图形能找到这样的一条直线，使图形沿这条直线折叠，直线两旁的部分能够互相重合，所以
是轴对称图形．
故选：B．
2．下列等式从左到右的变形是因式分解的是（
A．x2+3x＝x（x+3）
）
B．（x+y）（x﹣y）＝x2﹣y2
D．6xy2＝3x•2y2
2
2
2
C．x +2xy+y ﹣1＝（x+y） ﹣1
【分析】把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因
1 / 15

式，据此进行判断即可．
【解答】解：x2+3x＝x（x+3）符合因式分解的定义，则 A 符合题意；
2
2
（x+y）（x﹣y）＝x ﹣y 是乘法运算，则 B 不符合题意；
2
2
2
x +2xy+y ﹣1＝（x+y） ﹣1 中等号右边不是积的形式，则 C 不符合题意；
2
2
2
6xy ＝3x•2y 中 6xy 是单项式，则 D 不符合题意；
故选：A．
3．下列计算正确的是（
）
2
4
8
5
2
10
6
2
3
D．（3a）2＝6a2
A．（a ） ＝a
B．a •a ＝a
C．a ÷a ＝a
【分析】根据同底数幂的乘除法、幂的乘方与积的乘方法则进行解题即可．
2
4
8
【解答】解：A、（a ） ＝a ，故该项正确，符合题意；
5
2
7
B、a •a ＝a ，故该项不正确，不符合题意；
6
2
4
C、a ÷a ＝a ，故该项不正确，不符合题意；
2
2
D、（3a） ＝9a ，故该项不正确，不符合题意；
故选：A．
4．要使分式
A．x≠2
有意义，则 x 需满足的条件是（
）
B．x≠﹣2 C．x≠±2
D．x≠0
【分析】分式的分母不为零，即 x2﹣4≠0．
【解答】解：由分式有意义的条件可知：x2﹣4≠0，
∴x≠±2，
故选：C．
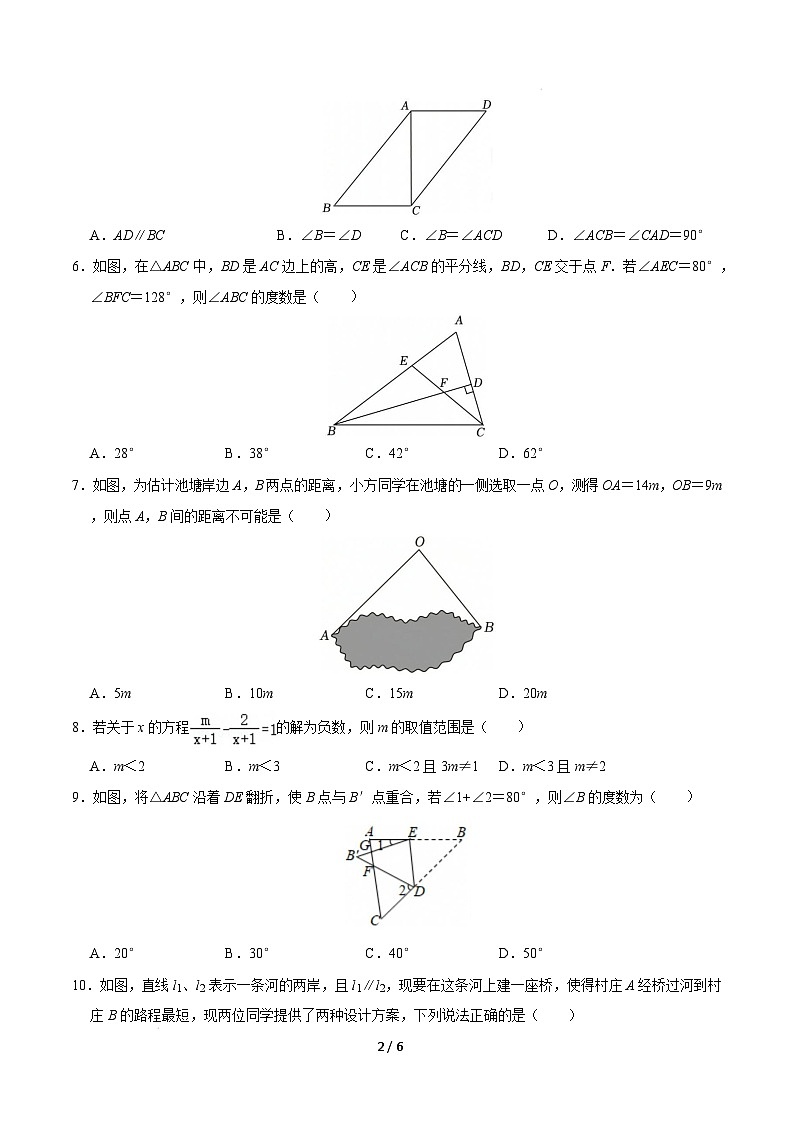
5．如图，在四边形 ABCD 中，AC 为对角线，AB＝DC，如果要证得△ABC 与△CDA 全等，那么可以添加
的条件是（
）
A．AD∥BC
B．∠B＝∠D
C．∠B＝∠ACD
D．∠ACB＝∠CAD＝90°
【分析】对于选项 A，根据 AD∥BC 得∠ACB＝∠CAD，由于 AB＝DC，AC＝CA，∠ACB＝∠CAD 不符
2 / 15

合全等三角形的判定条件，进而可对该选项进行判断；对于选项 B，由于 AB＝DC，AC＝CA，∠B＝∠D
不符合全等三角形的判定条件，进而可对该选项进行判断；对于选项 C，由于 AB＝DC，AC＝CA，∠B
＝∠ACD 不符合全等三角形的判定条件，进而可对该选项进行判断；对于选项 D，根据∠ACB＝∠CAD
＝90° 得△ABC 和△CDA 均为直角三角形，由于 AB＝DC，AC＝CA 符合全等三角形的判定条件，进而
可对该选项进行判断，综上所述即可得出答案．
【解答】解：对于选项 A，
∵AD∥BC，
∴∠ACB＝∠CAD，
根据 AB＝DC，AC＝CA，∠ACB＝∠CAD，不能判定△ABC 与△CDA 全等，
故选项 A 不符合题意；
对于选项 B，
根据 AB＝DC，AC＝CA，∠B＝∠D，不能判定△ABC 与△CDA 全等，
故选项 B 不符合题意；
对于选项 C，
根据 AB＝DC，AC＝CA，∠B＝∠ACD，不能判定△ABC 与△CDA 全等，
故选项 C 不符合题意；
对于选项 D，
∵∠ACB＝∠CAD＝90°，
∴△ABC 和△CDA 均为直角三角形，
在 Rt△ABC 和 Rt△CDA 中，
，
∴Rt△ABC≌Rt△CDA（HL），
故选 D 符合题意，
故选：D．
6．如图，在△ABC 中，BD 是 AC 边上的高，CE 是∠ACB 的平分线，BD，CE 交于点 F．若∠AEC＝80°，
∠BFC＝128°，则∠ABC 的度数是（
）
3 / 15

A．28°
B．38°
C．42°
D．62°
【分析】根据∠BFC 的度数以及 BD⊥AC，可求出∠ACE 度数，进而得出∠ACB 度数，再结合∠AEC 度
数，求出∠A 度数，最后利用三角形的内角和定理即可解题．
【解答】解：因为 BD 是 AC 边上的高，
所以∠BDC＝90°．
又∠BFC＝128°，
所以∠ACE＝128°﹣90°＝38°，
又∠AEC＝80°，
则∠A＝62°．
又 CE 是∠ACB 的平分线，
所以∠ACB＝2∠ACE＝76°．
故∠ABC＝180°﹣62°﹣76°＝42°．
故选：C．
【点评】本题考查角平分线的定义及三角形的内角和定理，利用外角求出∠ACE 的度数是解题的关键．
7．如图，为估计池塘岸边 A，B 两点的距离，小方同学在池塘的一侧选取一点 O，测得 OA＝14m，OB＝9m
，则点 A，B 间的距离不可能是（
）
A．5m
B．10m
C．15m
D．20m
【分析】三角形三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边，由此得到 5
＜AB＜23，即可得到答案．
【解答】解：由三角形三边关系定理得：14﹣9＜AB＜14+9，
4 / 15

∴5＜AB＜23，
∴A，B 间的距离不可能是 5m．
故选：A．
8．若关于 x 的方程
的解为负数，则 m 的取值范围是（
B．m＜3 C．m＜2 且 3m≠1 D．m＜3 且 m≠2
【分析】先银分式方程求得解为 x＝m﹣3，再根据方程银为负数和分式有意义条件列不等式求解即可．
）
A．m＜2
【解答】解：
，m﹣2＝x+1，x＝m﹣3，
∵原方程解为负数，
∴m﹣3＜0，
∴m＜3，
∵x+1≠0，
∴m﹣3+1≠0，
∴m≠2，
∴m＜3 且 m≠2，
故选：D．
9．如图，将△ABC 沿着 DE 翻折，使 B 点与 B′点重合，若∠1+∠2＝80°，则∠B 的度数为（
）
A．20°
B．30°
C．40°
D．50°
【分析】根据翻折的性质可得∠BED＝∠B'ED，∠BDE＝∠B'DE，结合平角的定义可求解∠BED+∠BDE
的度数，再利用三角形的内角和定理可求解∠B 的度数．
【解答】解：由翻折可知：∠BED＝∠B'ED，∠BDE＝∠B'DE，
∵∠1+∠BED+∠B'ED＝180°，∠2+∠BDE+∠B'DE＝180°，
∴∠1+2∠BED+∠2+2∠BDE＝360°，
∵∠1+∠2＝80°，
∴2∠BED+2∠BDE＝280°，
∴∠BED+∠BDE＝140°，
5 / 15

∵∠BED+∠BDE+∠B＝180°，
∴∠B＝180°﹣140°＝40°．
故选：C．
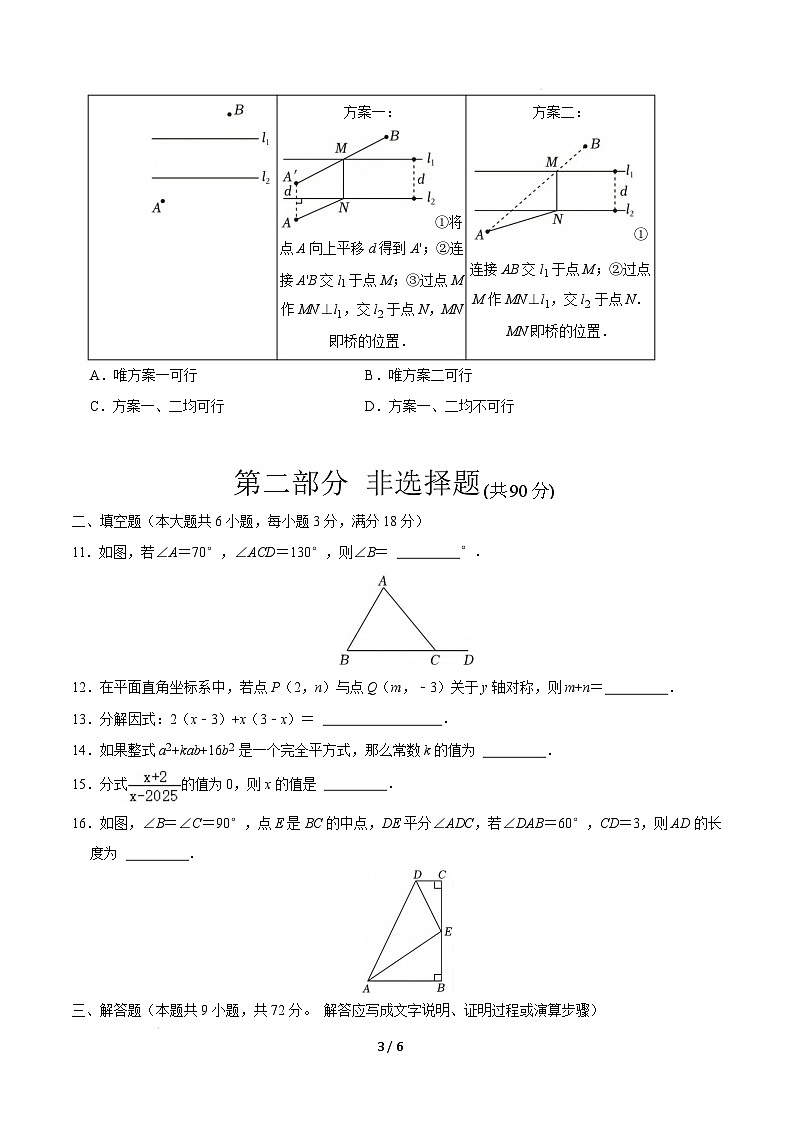
10．如图，直线 l 、l 表示一条河的两岸，且 l ∥l ，现要在这条河上建一座桥，使得村庄 A 经桥过河到村
1
2
1
2
庄 B 的路程最短，现两位同学提供了两种设计方案，下列说法正确的是（
）
方案一： 方案二：
①将
①
点 A 向上平移 d 得到 A'；②连
接 A'B 交 l1 于点 M；③过点 M
作 MN⊥l ，交 l 于点 N，MN
连接 AB 交 l1 于点 M；②过点
M 作 MN⊥l ，交 l 于点 N．
1
2
1
2
MN 即桥的位置．
即桥的位置．
B．唯方案二可行
D．方案一、二均不可行
A．唯方案一可行
C．方案一、二均可行
【分析】因为河宽是确定的，要使村庄 A 经桥过河到村庄 B 的路程最短，只要 AN+BM 最短即可，可利
用平移解决问题．
【解答】解：河宽是确定的，要使村庄 A 经桥过河到村庄 B 的路程最短，只要 AN+BM 最短即可．
∵AA'垂直于河岸 l2，AA′＝d，
连接 BA′，与另一条河岸相交于 M，作 MN⊥直线 l1，
由平移的性质，知 MN∥AA′，且 MN＝AA′＝d，MA′＝NA，
根据“两点之间线段最短”，BA′最短，即 AN+BM 最短．
故方案一符合题意，
故选：A．
第二部分 非选择题(共 90 分)
二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分）
11．如图，若∠A＝70°，∠ACD＝130°，则∠B＝
60 °．
6 / 15

【解答】解：∵∠A＝70°，∠ACD＝130°，
∴∠B＝130°﹣70°＝60°．
故答案为：60．
12．在平面直角坐标系中，若点 P（2，n）与点 Q（m，﹣3）关于 y 轴对称，则 m+n＝ ﹣5
【解答】解：∵点 P（2，n）与点 Q（m，﹣3）关于 y 轴对称，
∴m＝﹣2，n＝﹣3．
．
∴m+n＝﹣2+（﹣3）＝﹣5．
故答案为：﹣5．
13．分解因式：2（x﹣3）+x（3﹣x）＝
【解答】解：2（x﹣3）+x（3﹣x）
＝2（x﹣3）﹣x（x﹣3）
（x﹣3）（2﹣x）
．
＝（x﹣3）（2﹣x），
故答案为：（x﹣3）（2﹣x）．
2
2
14．如果整式 a +kab+16b 是一个完全平方式，那么常数 k 的值为
±8
．
2
2
2
2
2
【解答】解：a +kab+16b ＝（a±4b） ＝a ±8ab+16b ，
∴kab＝±8ab，
∴k＝±8，
故答案为：±8．
15．分式
的值为 0，则 x 的值是
﹣2
．
【解答】解：由题可知，
x+2＝0 且 x﹣2025≠0，
解得 x＝﹣2．
故答案为：﹣2．
16．如图，∠B＝∠C＝90°，点 E 是 BC 的中点，DE 平分∠ADC，若∠DAB＝60°，CD＝3，则 AD 的长
度为 12
．
7 / 15

【解答】解：延长 DE、AB 交于 F，
∵∠ABC＝∠C＝90°，
∴∠EBF＝∠C＝90°，
∵点 E 是 BC 的中点，
∴BE＝CE，
在△BEF 和△CED 中，
，
∴△BEF≌△CED（SAS），
∴BF＝CD＝3，EF＝ED，
∵CD∥AB，∠DAB＝60°，
∴∠ADC＝180°﹣∠DAB＝120°，
∵DE 平分∠ADC，
∴∠ADE＝ ∠ADC＝60°，
∴∠F＝∠DAF＝∠ADF＝60°，
∵∠EBF＝90°，∠BEF＝90°﹣∠F＝30°，
∴ED＝EF＝2BF＝6，
∴AD＝DF＝2ED＝12，
故答案为：12．
8 / 15

三、解答题（本题共 9 小题，共 72 分。 解答应写成文字说明、证明过程或演算步骤）
17．（本小题满分 4 分）（12a4﹣8a3+4a2）÷（2a）2．
4
3
2
2
【解答】解：原式＝（12a ﹣8a +4a ）÷4a
＝3a2﹣2a+1
18．（本小题满分 4 分）解方程：
．
【解答】解：原方程去分母得：3﹣x＝x﹣2+1，
解得：x＝2，
检验：当 x＝2 时，x﹣2＝0，
则 x＝2 是分式方程的增根，
故原方程无解
19．（本小题满分 6 分）先化简，再求值：
，其中 a＝3
【解答】解：
＝
•
•
＝
＝
，
当 a＝3 时，原式＝
＝
20．（本小题满分 6 分）已知：如图，∠B＝∠ADB＝∠ADE，∠C＝∠E．求证：AC＝AE．
【解答】证明：∵∠B＝∠ADB，∴AB＝AD，
在△ABC 和△ADE 中
，
9 / 15

∴△ABC≌△ADE（AAS），
∴AC＝AE
21．（本小题满分 8 分）如图，△ABC 三个顶点的坐标分别为 A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC 关于 x 轴对称的△A B C ；
1
1 1
（2）写出△A B C 各顶点坐标；
1
1 1
（3）试在 x 轴上求作一点 P，使点 P 到 A、B 两点的距离和最小，请标出 P 点，并写出点 P 的坐
标
．
【解答】解：（1）如图，△A B C 即为所求．
1
1 1
（2）由图可得，A （1，﹣1），B （4，﹣2），C （3，﹣4）．
1
1
1
（3）如图，连接 A1B，交 x 轴于点 P，连接 AP，
此时 PA+PB＝PA +PB＝A B，为最小值，
1
1
则点 P 即为所求．
由图可得，点 P 的坐标为（2，0）．
故答案为：（2，0）．
22．（本小题满分 10 分）列方程解应用题：
港珠澳大桥是世界上最长的跨海大桥，是被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大
10 / 15

国走向桥梁强国的里程碑之作．开通后从香港到珠海的车程由原来的 180 千米缩短到 50 千米，港珠澳大
桥的设计时速比按原来路程行驶的平均时速多 40 千米，若开通后按设计时速行驶，行驶完全程时间仅为
原来路程行驶完全程时间的 ，求港珠澳大桥的设计时速是多少．
【解答】解：设港珠澳大桥的设计时速是 x 千米/时，按原来路程行驶的平均时速是（x﹣40）千米/时．
依题意，得
．
解方程，得 x＝100．
经检验：x＝100 是原方程的解，且符合题意．
答：港珠澳大桥的设计时速是每小时 100 千米．
23．（本小题满分 10 分）数学活动课上，老师准备了若干个如图（1）的三种纸片．甲种纸片是边长为 a
的正方形，乙种纸片是边长为 b 的正方形，丙种纸片是长为 b、宽为 a 的长方形．
【观察发现】
用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成如图（2）的大正方形．观察图（2）的面积关系，
写出正确的等式：
【操作探究】
．
若要拼出一个面积为（a+b）（a+2b）的长方形，则需要甲种纸片
张，乙种纸片
张，丙
种纸片
张．（所拼图形不重叠无缝隙）
【拓展延伸】
2
2
两个正方形 ABCD、AEFG 如图（3）摆放，边长分别为 x，y，连接 CE，DF．若 x +y ＝52，DG＝2，求
图中阴影部分的面积．
【解答】解：【观察发现】
11 / 15

2
2
2
观察图形可知：图（2）的面积为：a +b +2ab，还可以表示为：（a+b） ，
2
2
2
∴正确的等式为：a +2ab+b ＝（a+b） ，
2
2
2
故答案为：a +2ab+b ＝（a+b） ；
【操作探究】
（a+b）（a+2b）
＝a2+2ab+ab+2b2
2
2
＝a +3ab+2b ，
∴需要甲种纸片 1 张，乙种纸片 2 张，丙种纸片 3 张，
故答案为：1，2，3；
【拓展延伸】
∵DG＝AD﹣AG＝2，AD＝x，AG＝y，
∴x﹣y＝2，
∴（x﹣y）2＝4，
2
2
x +y ﹣2xy＝4，
52﹣2xy＝4，
2xy＝48，
xy＝24，
2
2
2
∵（x+y） ＝x +y +2xy＝52+48＝100，
∴x+y＝10 或﹣10（不合题意，舍去），
∴阴影部分的面积
＝
＝
＝
＝
＝10×2﹣y﹣x
＝10×2﹣（x+y）
＝20﹣10
＝10．
12 / 15

24.（本小题满分 12 分）阅读材料，并解决问题：
我们知道，分子比分母小的分数叫做“真分数”，分子大于或等于分母的分数，叫做“假分数”．类似的，
我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之
为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．如
假分式；再如 这样的分式就是真分式．假分数 可以化成
似的，假分式也可以化为带分式（整式与真分式的和或差）的形式．
，
这样的分式就是
，
带分数的形式，类
如：
．
再如：
．
解决问题：
（1）分式
是
；（填“真分式”或“假分式”）
（2）将分式
化成带分式；
（3）当 a 为何值时，分式
【解答】解：（1）∵）分式
有最大值？最大值是多少？
的分子和分母的次数都是 1，
∴此分式是假分式，
故答案为：假分式；
（2）
＝
＝
＝
；
（3）由（2）可得：
，
13 / 15

∵a2≥0，
∴a2+1≥1，
∴当 a2+1＝1 时，
最大，
∴当 a＝0 时，
有最大值，最大值为：2+5＝7．
25．（本小题满分 12 分）在△ABC 中，
（1）如图①所示，如果∠A＝60°，∠ABC 和么 ACB 的平分线相交于点 P，那么∠BPC＝
；
（2）如图②所示，∠ABC 和∠ACD 的平分线相交于点 P，试说明∠BPC＝ ∠A；
（3）如图③所示，∠CBD 和∠BCE 的平分线相交于点 P，猜想∠BPC 与∠A 的关系并证明你的猜想.
【解答】解：（1）∵BP、CP 分别为∠ABC，∠ACB 的平分线，
∴∠ABC＝2∠PBC，∠ACB＝2∠PCB．
∵∠A＝180°﹣（∠ABC+∠ACB），
∴∠A＝180°﹣2（∠PBC+∠PCB），
∴∠A＝180°﹣2（180°﹣∠BPC），
∴∠A＝﹣180°+2∠BPC，
∴2∠BPC＝180°+∠A，
∴∠BPC＝90°+ ∠A＝90°+ ×60°＝120°，
故答案为：120°；
（2）∵BP 是∠ABC 的角平分线，
∴∠PBC＝ ∠ABC．
又∵CP 是∠ACD 的平分线，
14 / 15

∴∠PCD＝ ∠ACD，
∵∠ACD＝∠A+∠ABC，∠PCD＝∠BPC+∠PBC，
∴∠BPC＝ ∠A；
（3）90°﹣ ∠A．
证明：∵BP、CP 分别是∠ABC 与∠ACB 的外角平分线，
∴∠CBP＝ ∠CBD，∠BCP＝ ∠BCE，
∴∠CBP+∠BCP
＝
＝
＝
＝
∠CBD+ ∠BCE
（∠CBD+∠BCE）
（∠A+∠ACB+∠A+∠ABC）
（180°+∠A），
∴∠BPC＝180°﹣（∠CBP+∠BCP）
＝180°﹣ （180°+∠A）
＝90°﹣ ∠A．
15 / 15