广西南宁市第三中学2024-2025学年八年级上学期10月月考数学试卷(含解析)

这是一份广西南宁市第三中学2024-2025学年八年级上学期10月月考数学试卷(含解析)，共21页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
考试时间：120分钟；满分：120分
第I卷
一、选择题（本大题共12小题，每题3分，共36分）
1．2022年北京冬奥会冰雪运动项目的图标中，是轴对称图形的是（ ）
A． B． C． D．
2．下列式子中，是分式的是（ ）
A．B．C．D．
3．在平面直角坐标系中，点关于y轴对称的点的坐标是（ ）
A．B．C．D．
4．一个三角形的两边长为和，第三边长为奇数，则第三边长是（ ）
A．或B．或C．D．
5．下列变形正确的是（ ）
A．B．C．D．
6．下列计算中正确的是（ ）
A．B．C．D．
7．如图，，，，则的度数是（ ）
A．B．C．D．
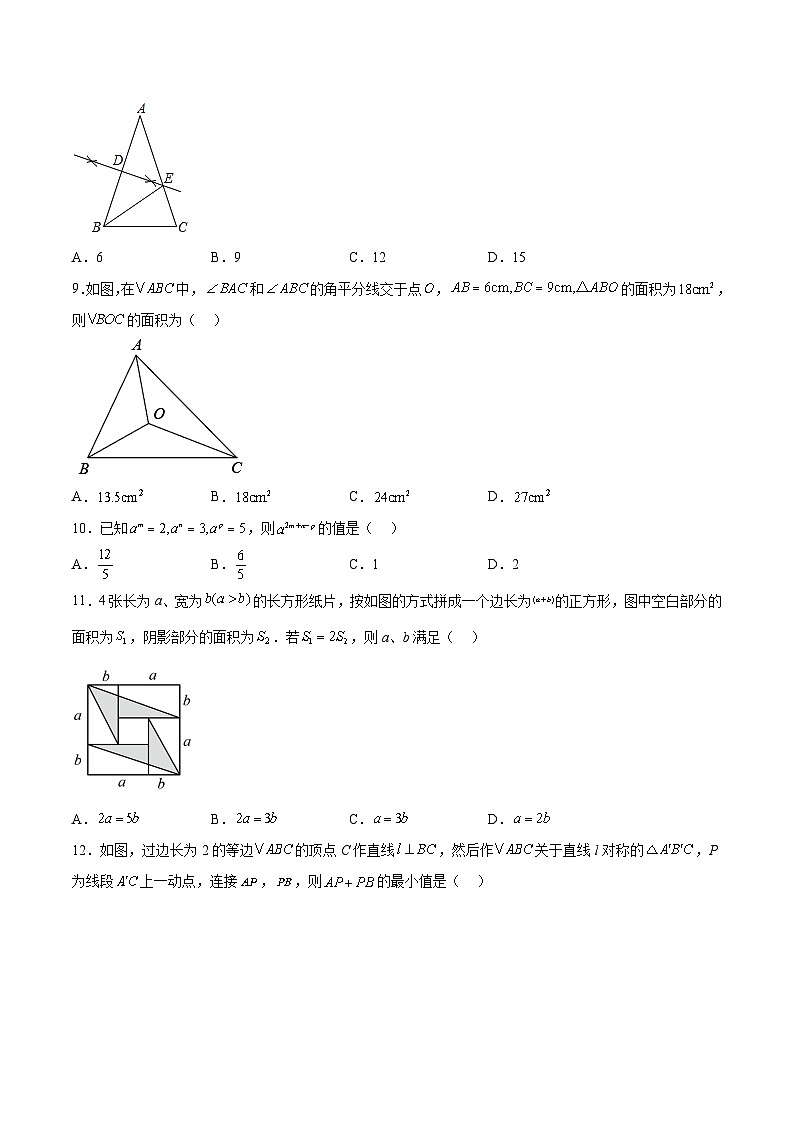
8．如图，在中，．依据尺规作图的痕迹，计算的周长为（ ）
A．6B．9C．12D．15
9．如图，在中，和的角平分线交于点，的面积为，则的面积为（ ）
A．B．C．D．
10．已知，则的值是（ ）
A．B．C．1D．2
11．4张长为a、宽为的长方形纸片，按如图的方式拼成一个边长为的正方形，图中空白部分的面积为，阴影部分的面积为．若，则a、b满足（ ）
A．B．C．D．
12．如图，过边长为2的等边的顶点C作直线，然后作关于直线l对称的，P为线段上一动点，连接，，则的最小值是（ ）
A．4B．3C．2D．1
第II卷
二、填空题（本大题共6小题，每题3分，共18分）
13．如图所示的自行车架设计成三角形，这样做的依据是三角形具有 ．
14．分式有意义，则x应满足的条件是 ．
15．分解因式： ．
16．如图，五个全等的等腰三角形拼成内外两个正五边形，则的度数为 ．
17．如图，中，，，点为中点，且，的平分线与的垂直平分线交于点，将沿（在上，在上）折叠，点与点恰好重合，则为 度．

18．如图，在中，厘米，厘米，点为AB的中点，点在线段上以厘米秒的速度由点向点运动，同时，点在线段CA上由点向点运动．当点的运动速度为 厘米/秒时，能够在某一时刻使与全等．
三．解答题（本大题共7小题，共66分）
19．计算：
(1)；
(2)．
20．先化简，再求值：，其中，．
21．如图，在平面直角坐标系中，的顶点均在正方形网格的格点上．
(1)画出关于x轴的对称图形；
(2)求的面积；
(3)若点P在x轴上，且点P到点A，B的距离相等，请直接写出点P的坐标．
22．如图，中，，，垂足为D．
(1)求作的角平分线，分别交，于点P，Q两点．（要求：尺规作图，保留作图痕迹，不写作法）；
(2)若，，求的长．
23．如图，中，，点D、E、F分别在边、AB、上，且，．
(1)求证：；
(2)若，求的度数．
24．数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：

(1)由图1和图2可以得到的等式为 （用含a，b的等式表示）；
(2)莉莉想用这三种纸片拼出一个面积为的大长方形，求需A，B，C三种纸片各多少张；
(3)如图3，S1，S2分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上，，．求图中阴影部分的面积．
25．已知：如图，都是等边三角形，相交于点O，点M、N分别是线段的中点．
(1)求证：；
(2)求的度数；
(3)求证：是等边三角形．
26．如图，在平面直角坐标系中，已知、分别在坐标轴的正半轴上．
(1)如图，若满足，以为直角顶点，AB为直角边在第一象限内作等腰直角，则点的坐标是___________；
(2)如图，若，点是的延长线上一点，以为直角顶点，BD为直角边在第一象限作等腰直角，连接，求证：；
(3)如图，设，的平分线过点，求的值．
1．D
解：A、不是轴对称图形，不符合题意；
B、不是轴对称图形，不符合题意；
C、不是轴对称图形，不符合题意；
D、是轴对称图形，符合题意；
故选：D
2．A
解：A、的分母含字母，故其是分式，故A符合题意；
B、是单项式，故B不符合题意；
C、是单项式，故C不符合题意；
D、是多项式，故D不符合题意．
故选：A．
3．B
解：点关于y轴对称的点的坐标是
故选：B．
4．C
解：设第三边长为，则由三角形三边关系定理得，
即．
∵第三边长为奇数，
∴，
故选： C．
5．C
解：A．，故选项错误，不符合题意；
B．不一定等于，故选项错误，不符合题意；
C．，故选项正确，符合题意；
D．不一定等于，故选项错误，不符合题意．
故选：C．
6．D
解：A． 与不是同类项，不能合并，故该选项不正确，不符合题意；
B． ，故该选项不正确，不符合题意；
C． ，故该选项不正确，不符合题意；
D． ，故该选项正确，符合题意．
故选D．
7．C
解：∵，，
∴，
∵，
∴，故C正确．
故选：C．
8．D
解：∵垂直平分，
∴，
∴的周长，
故选：D．
9．D
解：过点作于点，于点，如图，
∵平分，
∴，
∴，
∴．
故选：D．
10．A
解：当时，
，
故选：A．
11．D
解：，
，
∵，
∴，
整理，得，
∴，
∴．
故选D．
12．A
解：如图，连接，
∵与关于直线l对称，
∴，
∴，，
∴，
在和中，
，，，
∴，
∴，
∴，
由两点之间线段最短可知，当点P与点C重合，即点B，P，共线时，取得最小值，最小值为，
即的最小值为4．
故选：A．
13．稳定性
解：自行车的主框架采用了三角形结构，这样设计的依据是三角形具有稳定性，
故答案为：稳定性．
14．
解：分式有意义，即，
∴，
故答案为：．
15．
解：
，
故答案为：．
16．36
解：如图所示，五个全等的等腰三角形拼成内外两个正五边形，
∴，
∴，
∴，
故答案为：36．
17．108
解：如图，连接OB、OC，

∵∠BAC=54°，AO为∠BAC的平分线，
∴∠BAO=∠BAC=×54°=27°，
又∵AB=AC，
∴∠ABC=（180°-∠BAC）=×（180°-54°）=63°，
∵DO是AB的垂直平分线，
∴OA=OB，
∴∠ABO=∠BAO=27°，
∴∠OBC=∠ABC-∠ABO=63°-27°=36°，
∵AO为∠BAC的平分线，AB=AC，
∴△AOB≌△AOC（SAS），
∴OB=OC，
∴点O在BC的垂直平分线上，
又∵DO是AB的垂直平分线，
∴点O是△ABC的外心，
∴∠OCB=∠OBC=36°，
∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，
∴OE=CE，
∴∠COE=∠OCB=36°，
在△OCE中，∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°，
故答案为108．
18．4或6
解：设经过秒后，使与全等，
厘米，点为AB的中点，
厘米，
，
要使与全等，必须或，
即或，
解得：x=1或x=2，
x=1时，，；
x=2时，，；
即点的运动速度是厘米/秒或厘米/秒．
故答案为：或．
19．(1)
(2)
解：（1）（1）；
；
（2）
．
20．，
解：原式
，
当，时，
原式
．
21．(1)见解析
(2)4
(3)
（1）解：如图，为所作；
（2）解：的面积；
（3）解：如图点即为所作，P点坐标为．
22．(1)见解析
(2)6
（1）解：如图，以点C为圆心，任意长为半径作弧，与，相交，得到两个交点，以两个交点为圆心，大于两个交点距离的一半为半径分别作弧，连接C与两弧的交点，为所作；
（2）解：平分，
，
，
，
，
，
．
23．(1)见解析
(2)
解：（1）证明：∵，
∴，
在和中，
，
∴．
（2）解：∵，且，，
∴，
∴，
∵，
∴，
∴，
∴，
∴的度数是．
24．(1)或
(2)需A纸片2张 B纸片2张 C纸片5张
(3)8
解：（1）（a+b）2=a2+2ab+b2或a2+2ab+b2=（a+b）2．
（2）（2a+b）（a+2b）
=2a2+4ab+ab+2b2
=2a2+5ab+2b2．
∴需A纸片2张，B纸片2张，C纸片5张．
（3）由题意得，p2+q2=20，p+q=6．
∵（p+q）2=p2+q2+2pq=62，
∴2pq=62-20=16．
∴pq=8．
∴S阴＝pq×2＝pq＝8．
25．(1)证明见解析；
(2)的度数是；；
(3)证明见解析．
（1）证明：∵都是等边三角形，
∴，
∴，
∴，
在和中
，
∴，
∴；
（2）解：∵，
∴，
∵等边三角形，
∴，
∴
，
∴，
∴的度数是；
（3）证明：∵，
∴，
又∵点M、N分别是线段的中点，
∴，，
∴，
在和中，
，
∴，
∴，
，
又，
∴，
∴，
∴，
∴是等边三角形．
26．(1)
(2)证明见解析
(3)
（1）解：∵，
∴，，
∴，，
∴，，
∴，，
过点作轴于，如图，
则，
∵，
∴，，
∴，
∵，，
∴，
∴，，
∴，
∴，
故答案为：；
（2）证明：如图，过作轴于，则，
∵，
∴，
∵，
∴是等腰直角三角形，
∴，
∵是等腰直角三角形，，
∴，
∵，，
∴，
∵，
∴，
∴，，，
∵，
∴，
∴，即，
∴，
∴是等腰直角三角形，
∴，
∵，，
∴；
（3）解：如图，过点作轴于，轴于，交的延长线于，
∵ ，
∴，
∵BD平分，，，
∴，
∴，
∵ ，
∴，
∴，
同理可得，，
∴，
∵，，，
∴
，
，
，
，
即．