专题五　微专题3　统计与成对数据的统计分析--2025年高考数学大二轮复习课件+讲义+专练

这是一份专题五　微专题3　统计与成对数据的统计分析--2025年高考数学大二轮复习课件+讲义+专练，文件包含专题五微专题3统计与成对数据的统计分析--2025年高考数学大二轮专题复习课件pptx、专题五微专题3统计与成对数据的统计分析--2025年高考数学大二轮专题复习强化练习docx、专题五微专题3统计与成对数据的统计分析--2025年高考数学大二轮专题复习教师版docx、专题五微专题3统计与成对数据的统计分析--2025年高考数学大二轮专题复习学生版docx等4份课件配套教学资源，其中PPT共60页， 欢迎下载使用。
高考对本讲内容的考查往往以实际问题为背景，考查随机抽样与用样本估计总体、经验回归方程的求解与运用、独立性检验问题，常与概率综合考查，中等难度.
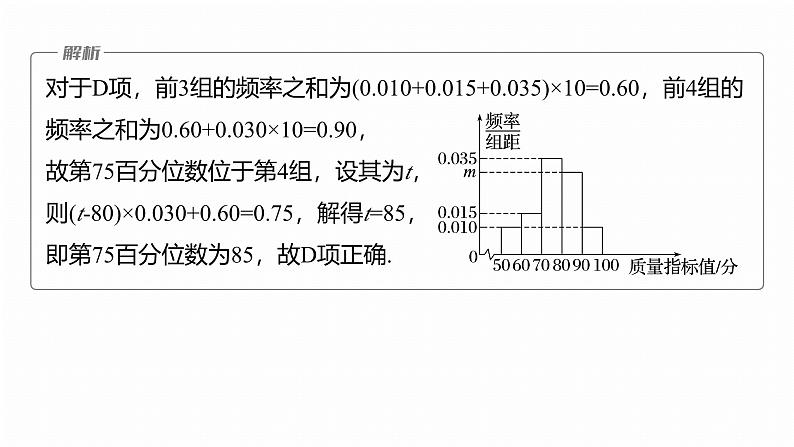
　(1)(多选)(2024·泰安模拟)某灯具配件厂生产了一种塑胶配件，该厂质检人员某日随机抽取了100个该配件的质量指标值(单位：分)作为一个样本，得到如图所示的频率分布直方图，则(同一组中的数据用该组区间的中点值作代表A.m=0.030B.样本质量指标值的平均数为75C.样本质量指标值的众数小于其平均数D.样本质量指标值的第75百分位数为85
(1)对于给出的统计图表，一定要结合问题背景理解图表意义.(2)频率分布直方图中纵坐标不要误以为是频率.
(1)(多选)海口市始终坚持生态优先，绿色低碳发展，空气质量长期领“鲜”全国.数据显示，2023年海口市空气质量创历史最高水平，位居全国168个重点城市之首.生活中常用空气质量指数(AQI)描述空气质量，AQI越小，表示空气质量越好.下表为2024年3月18日~3月24日一周内海口市和同为空气质量排行榜前十的“某市”的空气质量指数(AQI)，这组数据中，以下表述正确的是A.海口市这一周AQI的平均数为22B.“某市”这一周AQI的中位数为40C.两市这一周AQI的方差或标准差可以 反映出两市空气质量变化的稳定情况D.海口市这一周AQI的方差大于“某市”这一周AQI的方差
(2)(2024·温州模拟)2024年之前某淀粉厂只生产食品淀粉，下表为近几年年投入资金x(万元)与年收益y(万元)的8组数据：
①用y=bln x+a模拟生产食品淀粉年收益y与年投入资金x的关系，求出非线性经验回归方程；
②为响应国家“加快调整产业结构”的号召，该企业又自主研发出一种药用淀粉，预计其收益为投入的10%.2024年该企业计划投入200万元用于生产两种淀粉，求年收益的最大值(精确到0.1万元).
(2024·石家庄模拟)在推动电子制造业高质量发展的大环境下，某企业统筹各类资源，进行了积极的改革探索.下表是该企业每月生产的一种核心产品的产量x(3≤x≤15)(件)与相应的生产总成本y(万元)的四组对照数据.
(1)在下表中填写经验回归方程②的残差，根据残差分析，判断哪一个经验回归方程更适宜作为y关于x的经验回归方程，并说明理由；
②记该月的成本利润率为p，在(1)中选择的经验回归方程下，求p的估计值.(结果保留2位小数)
(2)若该班级共有36名学生，请完成列联表，并依据小概率值α=0.005的独立性检验，分析学生期末统考中的数学成绩与建立个性化错题本是否有关？
(1)χ2越大两分类变量无关的可能性越小，推断犯错误的概率越小，通过表格查得无关的可能性.(2)在犯错误的概率不大于0.01的前提下认为两个变量有关，并不是指两个变量无关的可能性为0.01.
(2024·福州模拟)人的性格可以大体分为“外向型”和“内向型”两种，某中学为了了解这两种性格特征与人的性别是否存在关联，采用简单随机抽样的方法抽取90名学生，得到如下数据：
(1)以上述统计结果的频率估计概率，从该校男生中随机抽取2人、女生中随机抽取1人担任志愿者.设这三人中性格外向型的人数为X，求X的数学期望；
一、单项选择题1.(2024·南通模拟)某工厂利用随机数表对生产的50个零件进行抽样测试，先将50个零件进行编号，编号分别为01，02，…，50，从中抽取5个样本，下面提供随机数表的第1行到第2行：66　67　40　37　14　64　05　71　11　05　6509　95　86　68　76　83　20　37　9057　16　03　11　63　14　90　84　45　21　7573　88　05　90　52　23　59　43　10若从表中第1行第9列开始向右依次读取数据，则得到的第4个样本编号是A.10B.09C.71D.20
2.(2024·张家口模拟)现有一组数据x1，x2，…，xn，将这组数据按照从小到大的顺序排列，则去掉第一个数和最后一个数后，下列统计量一定不变的是A.平均数B.中位数C.方差D.极差
3.某工厂为了调查工人文化程度与月收入的关系，随机抽取了部分工人，得到如下列联表(单位：人)：
根据表中数据，下列结论中正确的是A.100块稻田亩产量的中位数小于1 050 kgB.100块稻田中亩产量低于1 100 kg的稻田所占比例超过80%C.100块稻田亩产量的极差介于200 kg至300 kg之间D.100块稻田亩产量的平均值介于900 kg至1 000 kg之间
5.(2024·新课标全国Ⅱ)某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量(单位：kg)并整理得下表：
6.(2024·秦皇岛模拟)某校为了解本校高一男生身高和体重的相关关系，在该校高一年级随机抽取了7名男生，测量了他们的身高和体重得下表：
由表格制作成如图所示的散点图：
二、多项选择题7.(2024·安阳模拟)某研究机构为了探究过量饮酒与患疾病A是否有关，调查了400人，得到如图所示的2×2列联表，其中b=12a，则
11.(2024·开封模拟)某学校有A，B两家餐厅，A餐厅有2种套餐选择，B餐厅有4种套餐选择，且这6种套餐各不相同.A餐厅距离教学楼相比于B餐厅要近很多，经调查发现，100名不同性别的学生选择餐厅用餐的情况如下：
(1)求某天甲、乙两名同学选择同一套餐用餐的概率；
12.(2024·柳州模拟)某企业为了对一批新研发的产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据(xi，yi)(i=1，2，3，4，5，6)，如表所示：
14.(多选)(2024·海口模拟)已知甲、乙两组样本各有10个数据，甲、乙两组数据合并后得到一组新数据，下列说法正确的是A.若甲、乙两组数据的平均数都为a，则新数据的平均数等于aB.若甲、乙两组数据的极差都为b，则新数据的极差可能大于bC.若甲、乙两组数据的方差都为c，则新数据的方差可能小于cD.若甲、乙两组数据的中位数都为d，则新数据的中位数等于d