2024~2025学年天津市南开区九年级上学期期末考试数学试卷（解析版）

这是一份2024~2025学年天津市南开区九年级上学期期末考试数学试卷（解析版），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷（选择题 共36分）
一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（ ）
A. 6666B. 9999C. 6669D. 6699
【答案】D
【解析】将图形旋转180度后与原图重合的只有D项，故D项符合要求，
故选：D．
2. 下列事件是必然事件的是（ ）
A. 射击运动员射击一次，命中十环
B. 任意一个五边形的外角和等于
C. 任意画两个面积相等的三角形，这两个三角形全等
D. 个同学参加一个聚会，他们中至少有两个同学的生日是同月同日
【答案】D
【解析】A选项：射击运动员射击一次，命中十环是随机事件，故A选项不符合题意；
B选项：因为任意一个凸多边形的外角和都等于，所以任意画一个五边形的外角和等于，是不可能事件，故B选项不符合题意；
C选项：作意画两个面积相等的三角形，这两个三角形全等是一个随机事件，故C选项不符合题意；
D选项：闰年有天，所以个同学参加一个聚会，他们中至少有两个同学的生日是同月同日，这个事件是必然事件，故D选项符合题意．
故选：D．
3. 如图，四边形和四边形相似，点的对应点分别为，则下列结论正确的是（ ）
A. B.
C. D.
【答案】A
【解析】四边形和四边形相似，
，，，，
又，
．
故选：A．
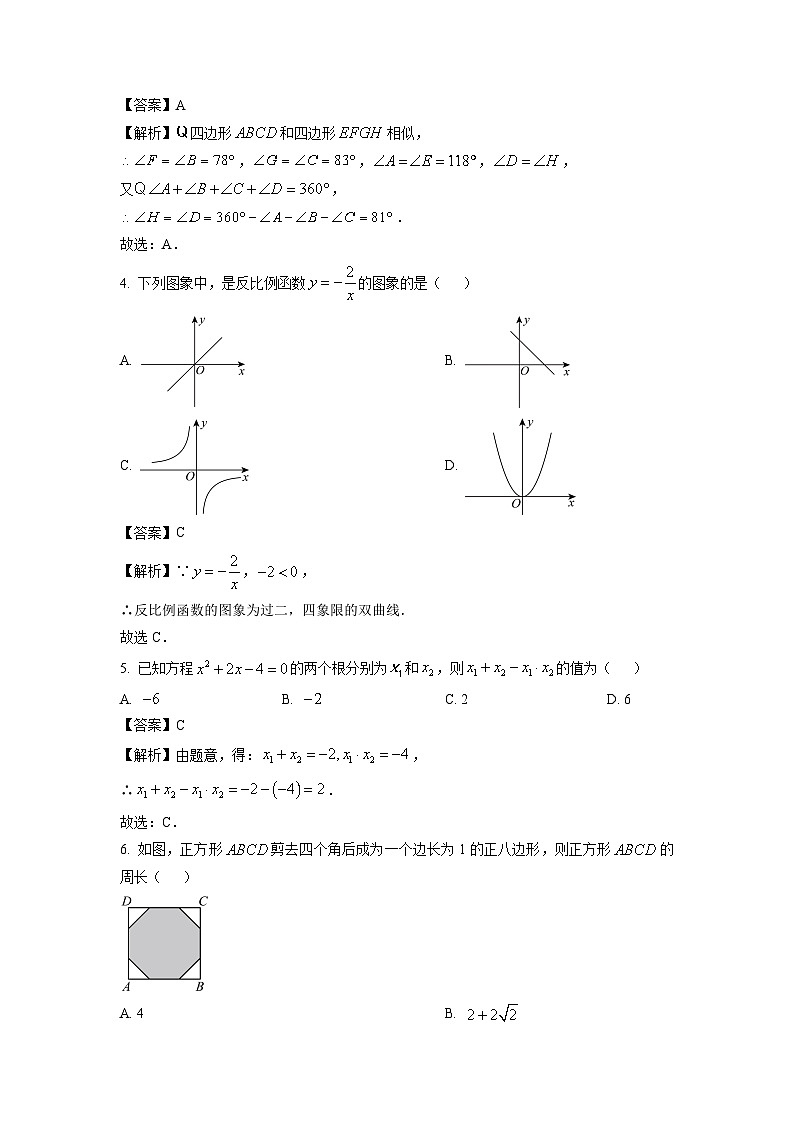
4. 下列图象中，是反比例函数的图象的是（ ）
A. B.
C. D.
【答案】C
【解析】∵，，
∴反比例函数的图象为过二，四象限的双曲线．
故选C．
5. 已知方程的两个根分别为和，则的值为（ ）
A. B. C. 2D. 6
【答案】C
【解析】由题意，得：，
∴．
故选：C．
6. 如图，正方形剪去四个角后成为一个边长为1的正八边形，则正方形的周长（ ）
A. 4B.
C. 8D.
【答案】D
【解析】如图，
由题意，得：，，
∴，
∴为等腰直角三角形，
∴，，
∴，
同理：，∴，
∴正方形的周长；
故选D．
7. 两年前生产1kg某种药品的成本是50元，随着生产技术的进步，现在生产1kg这种药品的成本是30元，如果这种药品成本的年平均下降率为，则可列方程为（ ）
A. B.
C. D.
【答案】C
【解析】由题意，可列方程为：；故选C．
8. 圆心角为，半径为3的扇形弧长为（ ）
A. B. C. D.
【答案】B
【解析】，
故选：B．
9. 如图，中，弦相交于点，，则的大小为（ ）
A. B. C. D.
【答案】B
【解析】∵，
∴，
∴；
故选B．
10. 如图，中，，将绕点顺时针旋转得到，点的对应点分别为，延长交于点，下列结论一定正确的是（ ）
A. B.
C. D.
【答案】D
【解析】记与相交于一点H，如图所示：
∵中，将绕点顺时针旋转得到，
∴
∵
∴在中，
∴
故D选项是正确的，符合题意；
设
∴
∵
∴
∴
∵不一定等于
∴不一定等于
∴不一定成立，
故B选项不正确，不符合题意；
∵不一定等于
∴不一定成立，
故A选项不正确，不符合题意；
∵将绕点顺时针旋转得到，
∴
∴
故C选项不正确，不符合题意；
故选：D.
11. 要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，则水管的长为（ ）
A. mB. 2mC. mD. 1m
【答案】A
【解析】如图，以水池中心为原点，原点与水柱落地处所在直线为x轴，水管所在直线为y轴，建立平面直角坐标系，
由题意，抛物线的顶点坐标为，与轴的一个交点坐标为，
设抛物线的解析式为：，
把代入抛物线解析式得：，∴，
∴，
∴当时，，
即水管的长为m；
故选A．
12. 如图，在中，，，．的内切圆与，分别相切于点，连接．以点为圆心，以适当长为半径作弧分别交于两点；分别以点为圆心，以大于的长为半径作弧，两条弧交于点；作射线．下列说法错误的是（ ）
A. 平分B. 点在射线上
C. D. 的半径为1
【答案】D
【解析】由作图可知：平分，故选项A正确；
∵是的内切圆，
∴点为三角形三条角平分线的交点，
∴点在射线上，故选项B正确；
连接，则：，
∵，
∴四边形为正方形，
∴，，
∴，故选项C正确；
∵，，，
∴，
设的半径为，则：，
∴，
∴，
∴，故选项D错误；
故选D．
第Ⅱ卷 （非选择题共84分）
二、填空题（本大题共6小题，每小题3分，共18分．请将答案直接填在答题纸中对应的横线上）
13. 如图，一个可以自由转动的转盘，转盘分成6个大小相同的扇形，颜色分为红、蓝、黄三种颜色．指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右侧的扇形）．任意转动转盘1次，当转盘停止转动时，指针指向蓝色扇形的概率为_______．
【答案】
【解析】任意转动转盘1次，共有6种等可能的结果，其中指针指向蓝色扇形的情况有2种，
∴．
14. 如图，在平面直角坐标系中，第一象限内的点在反比例函数（为常数，）的图象上，连接，过点作轴，垂足为，若的面积为2，则________．
【答案】4
【解析】∵点A在反比例函数（k为常数，）的图象上，轴，垂足为，∴根据反比例函数比例系数的几何意义得：，
∴，
∵的面积为2，∴，
∵，∴，
故答案为：4．
15. 两个相似三角形最短边分别为和，它们的周长之和为，那么较小三角形的周长为________（）．
【答案】18
【解析】∵两个相似三角形的最短边分别为和，
∴相似比为：，
∴两个三角形的周长比为：，
设较小三角形的周长为，较大三角形的周长为，
则：，
解得：，
∴较小三角形的周长为；
故答案为：18．
16. 圆的半径为13，、是圆的两条弦，，，，则与之间的距离为________．
【答案】7或17
【解析】如图所示，当在圆心O的同侧，过点O作，交于点E，交于点F，连接，
∵，
∴．
∵，
∴，
∴．
在中，，
中，，
∴；
如图所示，当在圆心O的异侧，过点O作，交于点E，作，交于点F，连接，
∵，
∴．
∵，
∴．
∵，
∴点E，O，F三点共线．
在中，，
在中，，
∴．
所以与之间的距离是7或17．
17. 如图，点是圆上一动点，弦，是的平分线，．当_______（度）时，四边形的面积最大，最大面积为_________．
【答案】
【解析】平分，，，
如图所示，过点作于点，
，
在中，＝30°，则，AB＝，
，
，
，为定值，
∴当最大时，四边形面积最大，
在中，AB边不变，其最长的高为过圆心与AB垂直（即AB的中垂线）与圆交于点，此时四边形面积最大．
∵，，
∴，
∴，
又∵，
∴为等边三角形，
∵为圆的直径，
∴，
，
，
四边形的最大面积为．
故答案为：；．
18. 如图，在每个小正方形的边长为1的网格中，每个小正方形的顶点叫做格点．均在格点上，点为线段与网格线的交点．
（Ⅰ）的长为_________；
（Ⅱ）请用无刻度的直尺，在如图所示的网格中，分别在线段上画出点，使得最小．简要说明点的位置是如何找到的（不要求证明）___________．
【答案】 5 取格点E，J，连接，，延长交于点M，交于点N，连接，点M，点N即为所求
【解析】（Ⅰ）；
（Ⅱ）如图，
取格点E，J，连接，，延长交于点M，交于点N，连接，点M，点N即为所求．
三、解答题（本大题共7小题，共66分．解答应写出文字说明、演算步骤或推理过程）
19. 在一个不透明的口袋中，有四个完全相同的小球，小球上分别标有数，，，．
（1）摇匀后，从口袋中随机摸出一个小球．若将摸出的小球上所标的数恰好是正数记为事件，求事件的概率；
（2）摇匀后，先从口袋中随机摸出一个小球（不放回），再从余下的三个小球中随机摸出一个小球．若将两次摸出的小球上所标的数之和等于记为事件．用列表或画树状图的方法，求事件的概率．
解：（1）在一个不透明的口袋中，随机摸出一个小球，小球上的数可能是，，，共种，这些数出现的可能性相等．
又出现的数为正数的可能有种，分别为或，；
（2）画树状图如下图所示：
从树状图可以看出共有个可能的结果，即
这些结果出现的可能性相等，
两次摸出小球上的数之和等于的结果有个，
即和（第一次摸出，且第二次摸出，或是第一次摸出，且第二次摸出），
．
20. 若点，在反比例函数（为常数，）的图象上．
（1）求：反比例函数的解析式和的值；
（2）填空：
①函数的图象在第________象限；
②该函数的图象的每一支上，随的增大而_________；
③在该函数的图象上分别取点和，如果，请将按从小到大的顺序排列，并用“”连接，其结果为__________．
解：（1）由题意，得：，
∴，反比例函数的解析式为：；
（2）∵，，
∴双曲线过二，四象限，在图象的每一支上，随的增大而增大；
∵点和在双曲线上，且，
∴；
故答案为：①二，四；②增大；③．
21. 在四边形中，，连接，点在上，连接，．
（1）如图1，求证：；
（2）如图2，若，，，，求的度数和的长．
（1）证明：∵，
∴，
∵，
∴；
（2）解：∵，
∴，
∴，
又∵，
∴，
∴；
∵，
∴，即，
∴．
22. 已知中，，为的弦，直线与相切于点．
（1）如图1，连接，若，直径与相交于点，求和的大小；
（2）如图2，若，，垂足为，与相交于点，，求线段的长．
解：（1）如图1所示，
∵为的切线，且为直径，
∴于点，即，
∵，
∴，
∴，
即于点，
∵于点，且为直径，
∴，，
∵，
∴，
∴，
∵，
∴；
（2）解：连接，
由（1）可知，且，
∵，，
∴，
∴在中，，，
∴，
设，则，
∴由勾股定理，
即，
解得，负值舍去，
即线段的长为．
23. 为了改善小区环境，某小区决定要在一块一边靠墙的空地上修建一个矩形绿化带，绿化带一边靠墙（的长不超过墙长），另三边用总长为40m的栅栏围住．设边长为m，绿化带的面积为．
（1）如图1，若墙长为19m．
①求与之间的函数关系式，并直接写出自变量的取值范围；
②当绿化带的面积为时，求的值；
③填空：当满足条件的绿化带的面积最大时，此时_________（m），绿化带的最大面积为_________（）；
（2）填空：如图2，若墙长为24m，当满足条件的绿化带的面积最大时，此时_________（m），绿化带的最大面积为_________（）．
解：（1）①由题意，，
∴，
∵墙长为19m，
∴；
②∵，
当时，，
解得：，
∵不合题意；
∴；
③∵，
∴当时，随的增大而增大，
∵，
∴当时，有最大值：；
故答案为：19，199.5；
（2）由题意，得：，
∴当时，有最大值为：200；
故答案为：20，200
24. 在平面直角坐标系中，点，点，其中，点在第一象限，且．将绕点逆时针旋转得到，点的对应点分别为，点恰在轴上．
（1）如图1，当时，求点的坐标和的长；
（2）如图2，当时，求点的坐标；
（3）当点组成的凸多边形为四边形时，将此四边形的面积记为．用含有的式子表示，并写出的取值范围（此问直接写出结果即可）．
解：（1）如图1，过点作轴于点，
∵是由逆时针旋转得到，且点在轴上，
∴，
∴，
且，
∴，
∴，
由勾股定理可知
解得；
∴点的坐标为；
（2）如图2，由（1）可知，且，
∵由旋转得到，
∴，
∴，
∴，
∴点的坐标为；
（3）如图， 当时，
绕点逆时针旋转得到，且轴，，，
轴，
，，
；
如图，当时，
绕点逆时针旋转得到，，，
，
；
如图，当时，
绕点逆时针旋转得到，，，
，，
．
25. 抛物线（为常数，）的顶点为，抛物线与轴相交于和两点，抛物线与轴相交于点．
（1）若，点在抛物线上，设点的横坐标为，且．
①求抛物线的解析式和顶点的坐标；
②若的面积与的面积相等，求的值；
（2）和是轴上的两动点，当的最小值为时，直接写出和的值．
解：（1）①，和代入，
得，解得，
∴，
∴，
∴；
②当时，，
∴，
设解析式为，则，解得，
∴
∵，
∴，
当点Q在下面时，
设解析式为，
则，
∴，
∴，
∵点Q为与抛物线的交点，
∴，
解得，或（舍去）；
当点Q在上面时，
作点A关于点B的对称点，
则，
同理可得的解析式为，
则，
解得，或；
综上，，或，或；
（2）和代入，
得，解得，
∴，
∴，
∴，
当时，，
∴，
取点C关于x轴的对称点，
向右作线段，使，连接，
则，，四边形是平行四边形，
∴，
∴，
当N运动到上时，，取得最小值，
∵，的最小值为，
∴，
∵，
∴解得，
∴，，
设直线的解析式为，
则，解得，
∴，
当时，，∴，解得，．