华东师大版（2024）八年级下册18.2 平行四边形的判定课前预习课件ppt

这是一份华东师大版（2024）八年级下册18.2 平行四边形的判定课前预习课件ppt，共24页。PPT课件主要包含了分别相等，互相平分，它是一个真命题，连接AC，BCDA已知，∵ABCD，ADBC，几何语言，平行四边形判定定理1，你能证明吗等内容，欢迎下载使用。
1.经历平行四边形判定定理的猜想与证明过程，体会 类比思想及探究图形判定方法的一般思路；（重点）2.掌握平行四边形的判定定理1和2，能根据不同条件 灵活选取适当的判定定理进行推理论证.（难点）
我们已经知道，如果一个四边形是平行四边形，那么它的两组对边分别平行，且是一个中心对称图形，具有如下一些性质： 1.两组对边___________； 2.两组对角___________； 3.两条对角线___________.
那么，怎样判定一个四边形是否是平行四边形呢？ 接下来，让我们一起来学习平行四边形的判定方法.
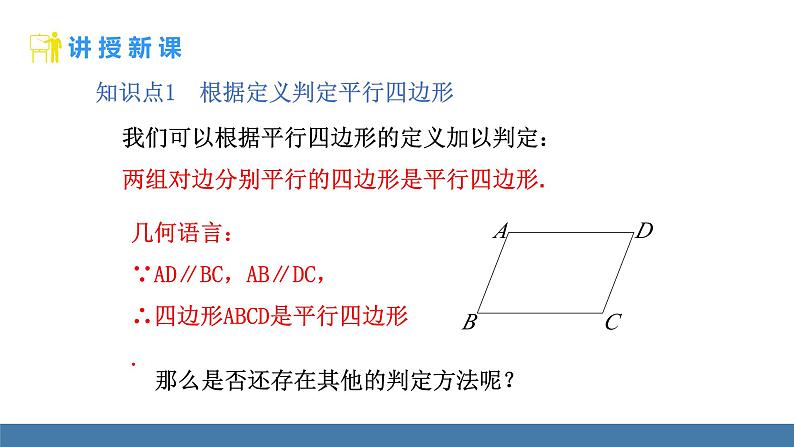
知识点1 根据定义判定平行四边形
我们可以根据平行四边形的定义加以判定：两组对边分别平行的四边形是平行四边形.
几何语言：∵AD∥BC，AB∥DC，∴四边形ABCD是平行四边形.
那么是否还存在其他的判定方法呢？
由平行四边形的性质“平行四边形的两组对边分别相等”，逆向思考，互换条件与结论，试写出它的逆命题.你认为它是一个真命题吗？
一个四边形是平行四边形
这个四边形的两组对边分别相等
一个四边形的两组对边分别相等
这个四边形是平行四边形
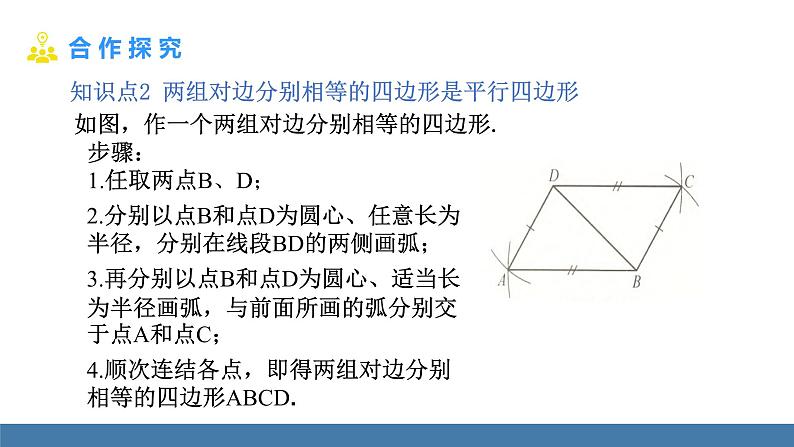
知识点2 两组对边分别相等的四边形是平行四边形
如图，作一个两组对边分别相等的四边形.
步骤： 1.任取两点B、D；
2.分别以点B和点D为圆心、任意长为半径，分别在线段BD的两侧画弧；
3.再分别以点B和点D为圆心、适当长为半径画弧，与前面所画的弧分别交于点A和点C；
4.顺次连结各点，即得两组对边分别相等的四边形ABCD.
把你作的四边形和其他同学作的进行比较，看看是否都是平行四边形.
可以发现，尽管每个人取的边长不一样，但只要对边分别相等，所作的就都是平行四边形.
由此可以得到判定平行四边形的一种方法： 平行四边形的判定定理1 两组对边分别相等的四边形是平行四边形.
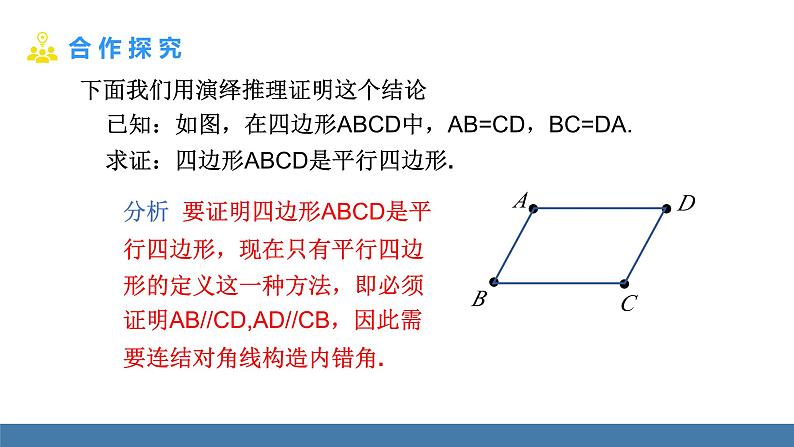
下面我们用演绎推理证明这个结论 已知：如图，在四边形ABCD中，AB=CD，BC=DA. 求证：四边形ABCD是平行四边形.
分析 要证明四边形ABCD是平行四边形，现在只有平行四边形的定义这一种方法，即必须证明AB//CD,AD//CB，因此需要连结对角线构造内错角.
在△ABC和△CDA中,
AB=CD (已知)，
AC=CA (公共边)，
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3，
∴AB∥ CD , AD∥ BC，
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
例1 如图，在Rt△MON中，∠MON＝90°.求证：四边形PONM是平行四边形．
证明：Rt△MON中，由勾股定理得(x－5)2＋42＝(x－3)2， 解得x＝8.∴PM＝11－x＝3，ON＝x－5＝3，MN＝x－3＝5.∴PM＝ON，OP＝MN，∴四边形PONM是平行四边形．
如图, AD⊥AC,BC⊥AC,且AB=CD.求证：四边形ABCD是平行四边形.
证明：在Rt△ABC和Rt△CDA中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL),∴BC=AD.又∵AB=CD,∴四边形ABCD是平行四边形．
问题 我们知道，两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢？
猜想1：一组对边相等的四边形是平行四边形.
知识点3 一组对边平行且相等的四边形是平行四边形
等腰梯形不是平行四边形，因而此猜想错误.
猜想2：一组对边平行的四边形是平行四边形.
梯形的上下底平行，但不是平行四边形，因而此猜想错误.
活动 如图，将线段AB向右平移BC长度后得到线段DC，连接 AD，BC，由此你能猜想四边形ABCD的形状吗？
四边形ABCD是平行四边形
猜想3：一组对边平行且相等的四边形是平行四边形.
作对角线构造全等三角形
已知：如图，在四边形ABCD中，AB=CD且AB∥CD.求证：四边形ABCD是平行四边形.
下面用推理演绎证明上述猜想.
证明：连接对角线AC.∵AB∥CD， ∴∠1=∠2.
∴△ABC≌△CDA(SAS)，
∴BC=DA .又∵AB= CD,
一组对边平行且相等的四边形是平行四边形.
“平行且相等”常用符号“ ”来表示.如图，AB=CD且AB// CD，可以记作“AB CD”，读作“AB平行且等于CD”
证明： ∵四边形ABCD是平行四边形，∴AD∥CB,即AF∥CE.又∵AF=CE，∴四边形AECF是平行四边形．
例2 如图 ，在▱ABCD中，点E、F分别在对边BC和DA上，且AF=CE.求证：四边形AECF是平行四边形.
分析 我们已经有了三种判定平行四边形的方法，根据已知条件AF=CE，若运用刚刚得到的判定定理2，则只需证明AF//CE.
例3 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，AE=DF，∠A=∠D，AB=DC．求证：四边形BFCE是平行四边形．
证明：∵AB=CD，∴AB+BC=CD+BC，即AC=BD，在△ACE和△DBF中， AC＝DB ,∠A＝∠D, AE＝DF ,∴△ACE≌△DBF(SAS)，∴CE=BF，∠ACE=∠DBF，∴CE∥BF，∴四边形BFCE是平行四边形．
【变式题】 如图，点C是AB的中点，AD=CE，CD=BE．（1）求证：△ACD≌△CBE；（2）求证：四边形CBED是平行四边形．
证明：（1）∵点C是AB的中点，∴AC=BC.在△ADC与△CEB中， AD＝CE , CD＝BE , AC＝CB ,∴△ADC≌△CEB（SSS），（2）∵△ADC≌△CEB，∴∠ACD=∠CBE，∴CD∥BE.又∵CD=BE，∴四边形CBED是平行四边形．
1.已知四边形ABCD中有四个条件：AB∥CD，AB=CD，BC∥AD，BC=AD，从中任选两个，不能使四边形ABCD成为平行四边形的选法是 （　　）A．AB∥CD，AB=CD B．AB∥CD，BC∥AD C．AB∥CD，BC=AD D．AB=CD，BC=AD
3.如图所示，△ABC是等边三角形，P是其内任意一点，PD//AB,PE//BC,PF//AC,若△ABC的周长为24，则PD+PE+PF= .
2.已知AD//BC ，要使这个四边形ABCD为平行四边形，需要增加条件 __ .
AD=BC或AB//CD
4.已知：如图，E,F分别是▱ABCD的边AD,BC的中点. 求证：BE=DF.
∵四边形ABCD是平行四边形，
∴AB∥CD，AD=BC
∵E,F分别是AD,BC的中点，
∴ED=BF,即ED BF.
∴四边形EBFD是平行四边形（一组对边平行且相等的四边形是平行四边形）.
∴BE=DF(平行四边形的对边分别相等).
5.如图，已知E，F，G，H分别是▱ABCD的边AB，BC，CD，DA上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形．
证明：在平行四边形ABCD中，∠A=∠C，AD=BC,又∵BF=DH，∴AH=CF.又∵AE=CG，∴△AEH≌△CGF（SAS），∴EH=GF.同理得△BEF≌△DGH（SAS），∴GH=EF，∴四边形EFGH是平行四边形．