9-通州 2024-2025第一学期初三数学期末试卷

这是一份9-通州 2024-2025第一学期初三数学期末试卷，共8页。试卷主要包含了填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
2025年1月
一、选择题（本题共8个小题，每小题2分，共16分）每题均有四个选项，符合题意的选项只有一个．
1. 在Rt△ABC中，，如果AC＝1，BC＝2，那么的值为
A．B．C．D．
2．如图，，，是⊙O上的三点，如果，那么的度数是
第4题图
第6题图
A．B．C．D．
第2题图
3．关于函数，，，的图象的共同点，下列说法正确的是
A．开口向上 B．都有最低点C．随增大而增大 D．对称轴是轴
4．如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，那么cs∠AOB的值是
A．B．C．D．
5. 如果二次函数的图象经过点，那么该图象必经过点
A．B．C．D．
6．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，如果，OD＝4，那么DC的长是
A．6B．4C．D．3
为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图，架在消防
车上的云梯AB可伸缩，也可绕点B转动，其底部B离地面的距离BC为2 m，
当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为10 m，
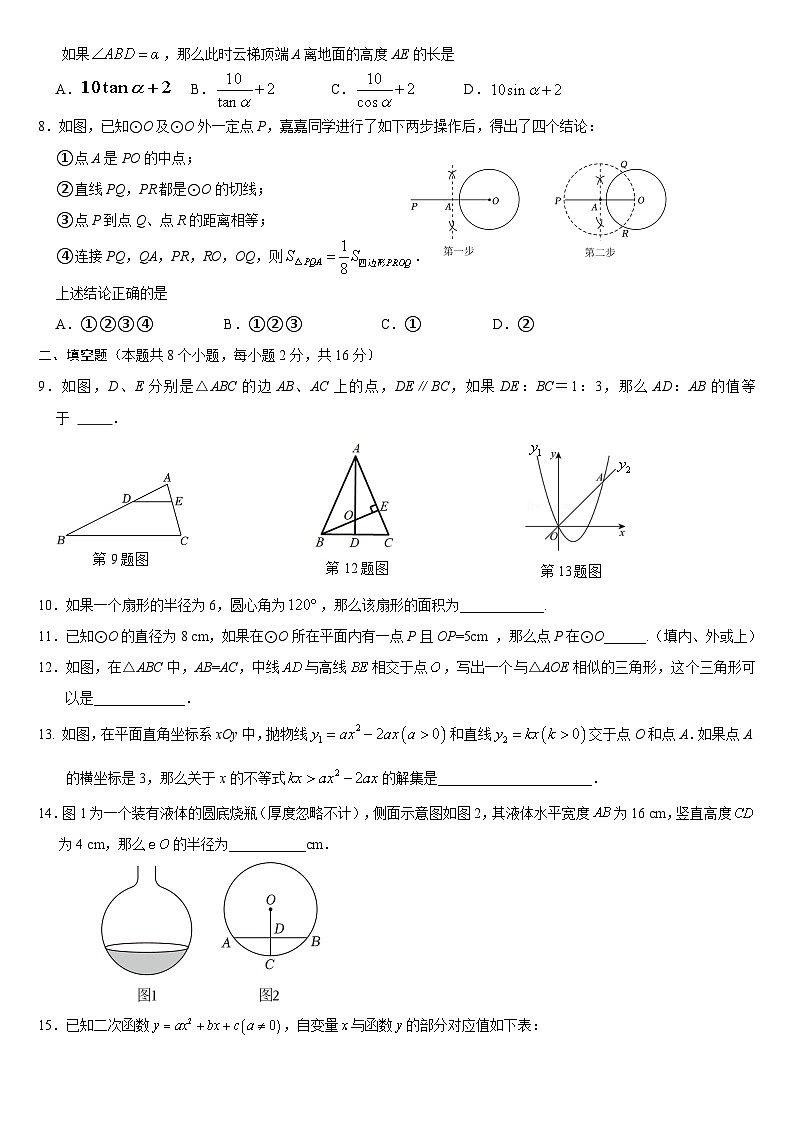
如果，那么此时云梯顶端A离地面的高度AE的长是
A．B．C．D．
8．如图，已知⊙O及⊙O外一定点P，嘉嘉同学进行了如下两步操作后，得出了四个结论：
①点A是PO的中点；
②直线PQ，PR都是⊙O的切线；
③点P到点Q、点R的距离相等；
④连接PQ，QA，PR，RO，OQ，则．
上述结论正确的是
A．①②③④ B．①②③ C．① D．②
二、填空题（本题共8个小题，每小题2分，共16分）
9．如图，D、E分别是△ABC的边AB、AC上的点，DE∥BC，如果DE：BC＝1：3，那么AD：AB的值等于 ．
第13题图
第12题图
第9题图
10．如果一个扇形的半径为6，圆心角为，那么该扇形的面积为____________.
11．已知⊙O的直径为8 cm，如果在⊙O所在平面内有一点P且OP=5cm ，那么点P在⊙O______.（填内、外或上）
12．如图，在△ABC中，AB=AC，中线与高线相交于点，写出一个与△AOE相似的三角形，这个三角形可以是_____________．
13. 如图，在平面直角坐标系xOy中，抛物线和直线交于点O和点A．如果点A的横坐标是3，那么关于x的不等式的解集是______________________．
14．图1为一个装有液体的圆底烧瓶（厚度忽略不计），侧面示意图如图2，其液体水平宽度为16 cm，竖直高度 为4 cm，那么的半径为___________cm．
15．已知二次函数，自变量与函数的部分对应值如下表：
关于的一元二次方程的解是__________________．
16. 小明同学想利用“∠A＝30°，AB＝6 cm，BC＝5cm”，这三个条件作△ABC．他先作出了∠A＝30°和AB＝6 cm，再作BC＝5 cm，那么AC的长是________________cm .
三、解答题（本题共68分，第17—24题每小题5分，第25、26题每小题6分，第27、28题每小题8分）解答应写出文字说明、演算步骤或证明过程．
17．计算：．
18．已知二次函数．
（1）写出此函数图象的开口方向、对称轴；
（2）请你判断点P（3，-4）是否在此二次函数的图象上；
（3）如果点A（，），B（，）（）均在该抛物线上，那么 ．（选填：“＞”“＝”或“＜”）
19. 如图，在△ABC中，，AD是△ABC的中线，如果AB＝6，AD=5，求的值.

20．如图，菱形ABCD的对角线AC和BD交于点O，分别过点A、B作AE∥BD，BE∥AC，AE和BE交于点E．
（1）求证：四边形AEBO是矩形；
（2）连接EC，当，时，求tan∠CEB的值．
已知：如图，在△ABC中，AB=AC.
求作： 射线AE，使得.
小靖同学的作法如下：
①以点为圆心，AB长为半径画圆，延长BA交⊙A于点D；
②作的角平分线交⊙A于点E；
= 3 \* GB3 ③作射线AE.
所以射线AE即为所求.
请你依据小靖同学设计的尺规作图过程，完成下列问题：
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明
证明：连接DC.
∵AB=AC，
∴点C在⊙A上.
∵BD是⊙A的直径，
∴（）（填推理依据）.
∵BE平分，
∴.
∴
∴（）（填推理依据）.
∵，
∴.（）（填推理依据）.
∴.
22．在矩形ABCD中，AB＝8，点G为边AD上一点，AG＝6，CE⊥BG于点E，．
（1）求证：△ABG∽△ECB；
（2）求证：E是BG的中点．
23．某学校物理实验室有一种演示桌，收起时桌面与一支架的夹角，打开时桌面与同一支架的夹角（桌面），已知支架cm，求桌面上升的高度约为多少cm？（桌面的厚度与前后移动的距离等因素不用考虑）（参考数据：，，，，，）.
24．如图，AB是⊙O的直径，弦CD⊥AB于点E，F是⊙O上一点，D是的中点，连结CF交OB于点G，连结BC．
（1）求证：GE＝BE；
（2）若AG＝6，BG＝4，求CD的长．
25．如图，在△ABC中，AB＝AC，O是AB的中点，到点O的距离等于的所有点组成图形G，图形G与边BC交于点D，过点D作DE⊥AC于点E．
（1）依题意补全图形，判断直线DE与图形G的公共点个数并加以证明；
（2）CA延长线交图形G于点F，如果，，求DE的长．

26．在平面直角坐标系xOy中，二次函数的图象经过点（2，c）．
（1）求此二次函数图象的对称轴；
（2）若二次函数的图象上存在两点A（，），B（，），其中，，且，求的取值范围．
27. 在△ABC中，，AM⊥BC于点M，D是线段BC上的动点（不与点B，C，M重合），将线段DM绕点D顺时针旋转得到线段DE．
（1）如图1，如果点E在线段AC上，求证：ME⊥AC；
（2）如图2，如果D在线段BM上，在射线MB上存在点F满足DF＝DC，连接AE，AF，EF，求证：AE⊥FE .

28．在平面直角坐标系xOy中，⊙O的半径是．对于点P和⊙O，给出如下定义：过点C的直线与⊙O交于不同的点M，N，如果点P为线段MN的中点，我们把这样的点P叫做关于MN的“弦中点”．
（1）如图1，已知点C（，）；
①点（，），（，），（，）中是关于MN的“弦中点”的是 ；
②若一次函数的图象上只存在一个关于MN的“弦中点”，求b的值；
如图2，若C（，），一次函数的图象上存在关于MN的“弦中点”，直接写出m的取值范围．

考生须知
1. 本试卷共 4 页，共三道大题，28 个小题,满分为 100 分，考试时间为 120 分钟 .
2. 请在试卷和答题卡上准确填写学校名称、班级、姓名 .
3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效 .
4. 在答题卡上，选择题、作图题用 2B 铅笔作答，其他试题用黑色字迹签字笔作答 .
5. 考试结束后，请将答题卡交回 .
0
1
2
3
5
0
0